Aufgaben zur Integralrechnung
Dieser Bereich der Website befindet sich im Umbau.
Betrachten Sie daher auch folgende Arbeitsblätter für mehr Aufgaben zu diesem Thema:
Inhaltsverzeichnis
1. Stammfunktionen
Berechne die nachfolgenden unbestimmten Integrale mit Hilfe der Substitutionsregel. Erstelle einen vollständigen und formal korrekten Rechenweg. Vergiss nicht auf die Rücksubstitution und die Integrationskonstante!
a) $\int\left(3\cdot \sin(2t+1)+1\right)\,dt$
b) $\int \frac{9s}{s^2+19}\,ds$
c) $\int \frac{\ln(3z)}{6z}\,dz$
#1128 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Berechne die nachfolgenden unbestimmten Integrale mit Hilfe der partiellen Integration. Vereinfache das Ergebniss so weit wie möglich (z. B. durch Herausheben oder durch Kürzen von Brüchen). Wandle Brüche nicht in Dezimalzahlen um!
a) $\int 3z\cdot \ln(7z)\,dz$
b) $\int 9x^2 \cdot e^{9x}\,dx$
c) $\int 9t\cdot \cos(4t+3)\,dt$
#1154 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Berechne das folgende unbestimmte Integral ohne Computereinsatz.
$$\int 2.48^x\cdot \sin(1.51x)\,dx$$
#1155 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Berechne das folgende unbestimmte Integral ohne Computereinsatz.
$$\int 3.2 t\cdot 1.88^t\,dt$$
#1157 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Berechne das folgende unbestimmte Integral ohne Computereinsatz.
$$\int 9 z\cdot \sqrt{8 z^2 + 26}\, dz$$
#1158 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Berechne das folgende unbestimmte Integral ohne Computereinsatz.
$$\int \frac{7}{(6s-13)^2}\,ds$$
#1193 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Berechne jeweils das unbestimmte Integral!
a) $\int (5t^2-2t+15)\,dt$
b) $\int \frac{2x^2-16}{10} \,dx$
#1194 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Gib an, ob die folgenden Aussagen richtig oder falsch sind.
Die Funktion $f(x)=3x^2$ besitzt unendlich viele Stammfunktionen.
Wenn $F$ eine Stammfunktion von $f$ ist, dann ist auch $F-5$ eine Stammfunktion von $f$.
Die Funktion $g(x)=5x^3$ besitzt unendlich viele unbestimmte Integrale.
Wenn $F_1$ und $F_2$ Stammfunktionen von $f\neq 0$ sind, dann ist auch $F_1+F_2$ eine Stammfunktion von $f$.
$F_1(x)=(x-2)^2$ und $F_2(x)=x^2-4x$ sind zwei Stammfunktionen derselben Funktion.
Wenn $F$ eine Stammfunktion von $f$ ist, dann ist auch $3\cdot F$ eine Stammfunktion von $f$.2. Hauptsatz der Differential- und Integralrechnung
Berechne die folgenden bestimmten Integrale. Die Argumente der Sinusfunktion sind hier (wie meistens außerhalb geometrischer Sachverhalte) im Bogenmaß (rad) gemessen.
a) $\int_{2.4}^{5.8} (3.1x^2+4.7x-8.4)\,dx $
b) $\int_{1.2}^{4.8} 2.9\cdot e^{0.81\cdot t} \,dt $
c) $\int_{0.24}^{1.04} \sin(3.1- 2.9 z) \,dz $
#1153 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Berechne die folgenden bestimmten Integrale mit Hilfe des Hauptsatzes der Differential- und Integralrechnung (ohne Computer).
a) $\int_{-4}^{2} (7 x^2 - 2 x+5)\,dx$
b) $\int_{-1.5}^{4.2} 1.5\cdot e^{0.47\cdot t}\,dt$
#1162 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Berechne mit Hilfe des Hauptsatzes der Differential- und Integralrechnung (ohne Computer) das folgende Integral. Achtung: Die verschiedenen Variablen im Integrand und im Differential sind beabsichtigt.
$$\int_{-8}^{3} (8 x-20)\,dt$$
#1163 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Gib an, ob die folgenden Aussagen allgemein gültig sind oder nicht.
$\int_{-a}^b f(x)\,dx=-\int_{b}^{-a} f(x)\,dx$
$\int_a^b \left( f(x)+g(x) \right)\,dx= \int_a^b f(x)\,dx +\int_a^b g(x)\,dx$
$\int_a^b f(x)\cdot g(x)\,dx= \int_a^b f(x)\,dx \cdot \int_a^b g(x)\,dx$
$\int_a^c f(x)\,dx= \int_a^b f(x)\,dx + \int_b^c f(x)\,dx$
$\int_a^b |\,f(x)\,|\,dx= \left| \int_a^b f(x)\,dx\right|$
$\int_a^a f(x)\,dx=0$3. Flächenberechnung
Ermittle den Flächeninhalt zwischen Funktionsgraph und $x$-Achse im Intervall $[1,5]$ so genau wie möglich.


Vorgegeben ist die Funktionsgleichung $f(x)=2.3+1.5x^2-1.2x^4$.
a) Berechne die beiden Nullstellen $x_1$ und $x_2$.
b) Berechne den Flächeninhalt zwischen Funktionsgraph und $x$-Achse im Intervall $[x_1,x_2]$.
c) Die Fläche aus Aufgabe b) soll durch eine vertikale Gerade so zerteilt werden, dass die rechte Teilfläche 38 % des gesamten Flächeninhalts aus Aufgabe b) besitzt. Bestimme die Stelle $x_T$, an welcher sich diese Gerade befinden muss. Für diese Aufgabe wird die Verwendung eines geeigneten Computerprogramms empfohlen.
Diese Aufgabe sollte vollständig mit Hilfe eines geeigneten Computerprogramms gelöst werden. Die Funktion $A(t)=4.3\cdot 0.68^t \cdot \sin(2.9t)$ wird ausschließlich im Intervall $[0,\infty)$ betrachtet. Das Funktionsargument des Sinus wird hier im Bogenmaß (rad) gemessen.
a) Ermittle das globale Maximum dieser Funktion (beide Koordinaten). Diese Aufgabe muss nicht zwingend analytisch gelöst werden.
b) Berechne die sechste Nullstelle, also jene Nullstelle, bei welcher die fünfte Teilfläche endet.
c) Berechne den absoluten Flächeninhalt zwischen Funktionsgraph und $x$-Achse im Intervall $[0,x_6]$, also die Summe der Flächeninhalte der ersten fünf Teilflächen.
Es sind die Funktionsgleichungen $f(x)=-1.01x^2+7.55x-7.15$ und $g(x)=0.2x+1.2$ vorgegeben.
a) Berechne die Schnittstellen $x_1$ und $x_2$ der beiden Funktionsgraphen.
b) Berechne den Flächeninhalt zwischen den beiden Funktionsgraphen im Intervall $[x_1,x_2]$.
Es ist die Funktion $E(t)=6.58\cdot 1.167^t$ sowie die Untergrenze $a=1.1$ vorgegeben. Berechne die Obergrenze $b$, sodass der Flächeninhalt zwischen Funktionsgraph und $t$-Achse im Intervall $[a,b]$ den Wert 38 FE besitzt. Wird für diese Aufgabe GeoGebra verwendet, so muss der Befehl NLöse eingesetzt werden.
Der Querschnitt eines Erdwalls, welcher als Hochwasserschutz entlang eines Flusses errichtet werden soll, kann durch den positiven Teil des Funktionsgraphen von $h(x)=2-0.12x^4$ beschrieben werden. Dabei werden $x$ und $h(x)$ jeweils in Metern gemessen. Die Länge des Erdwalls soll 0.96 km betragen.
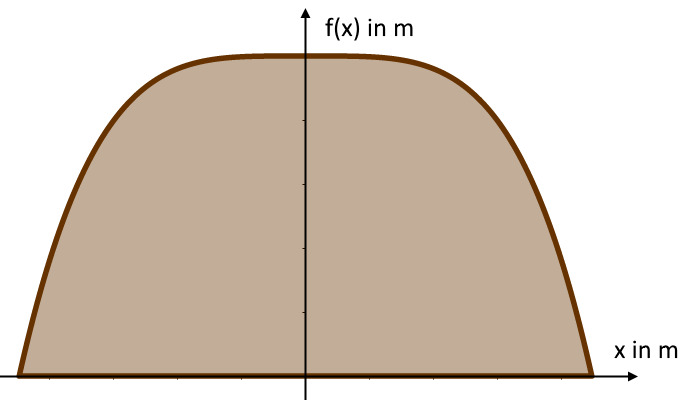

a) Bestimme die Basisbreite des Erdwalls (die Breite am Boden).
b) Bestimme den Flächeninhalt der Querschnittsfläche des Erdwalls.
c) Das verwendete Bodenmaterial hat die Dichte $\rho=1470\,\text{kg}/\text{m}^3$. Berechne, wie viele Tonnen davon für die Errichtung des Erdwalls nötig sind.
#315 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
In folgender Abbildung ist der blaue Funktionsgraph die obere Hälfte des Einheitskreises $f(x)=\sqrt{1-x^2}$. Der rote Graph ist jener der Funktion $g(x) = –x^4 + 1$.
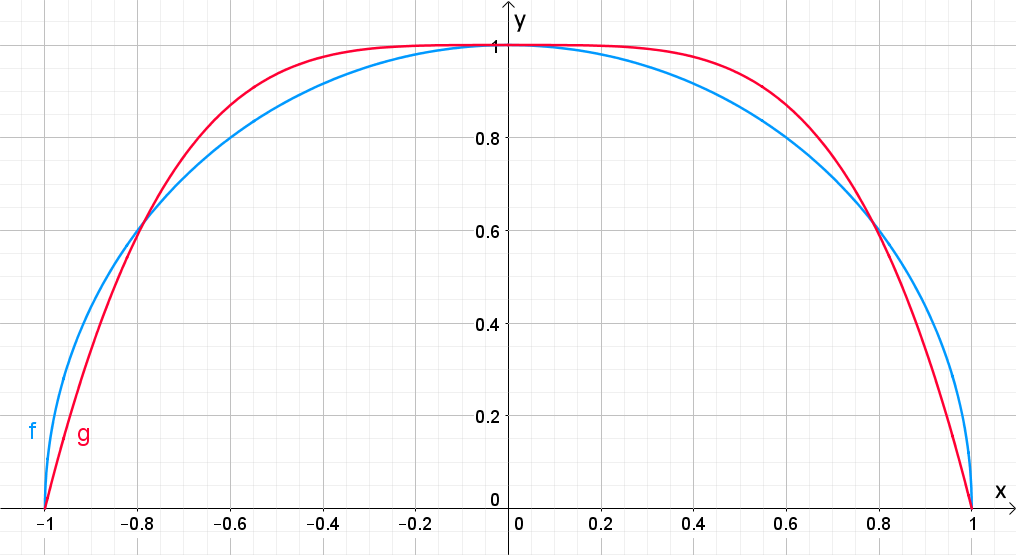
Argumentiere anhand mathematischer Berechnungen, welcher Funktionsgraph zusammen mit der x-Achse im Intervall $[-1;1]$ den größeren Flächeninhalt einschließt.
Ein Holztor wird gemäß der untenstehenden nicht maßstabsgetreuen Skizze gefertigt. Die Breite des Tors beträgt 2.89 m. Die Höhe beträgt an den Seiten 2.37 m. In der Mitte ist das Tor um 32 cm höher als an den Seiten.
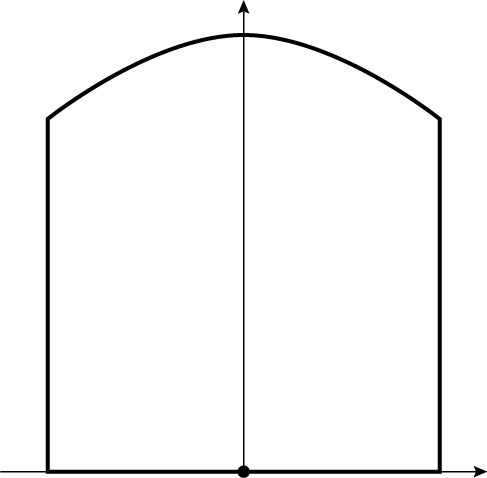

a) Bestimme die Funktionsgleichung jener quadratischen Funktion, durch welche die Oberkante des Tors beschrieben werden kann.
b) Berechne die Fläche des Holztors.
c) Berechne die Masse des Holztors, wenn dessen Dicke 6.4 cm beträgt und die Dichte des verwendeten Holzes 0.63 g/cm³ ist.
#986 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Die Breite der Sporthalle „The Wave“ in Singapur (siehe Foto, Bildquelle: https://www.structure-magazin.de/artikel/the-wave-sporthalle-in-singapur-32322/) beträgt 72 m (jene Seite, die am Foto sichtbar ist). Das Dach entspricht einer quadratischen Parabel. Es ist an den Seiten ca. 17 m hoch und in der Mitte ungefähr 27 m hoch. Die Länge der Halle beträgt 42 m.

a) Erstelle eine quadratische Funktion, durch welche der Verlauf des Daches beschrieben werden kann. Die Funktion soll symmetrisch bezüglich der y-Achse sein (um den Rechenaufwand gering zu halten).
b) Berechne das Volumen der Halle.
Die Form eines Wassertrogs kann näherungsweise durch den Graphen der Funktion $f(x)=57x^4$ beschrieben werden, wobei $x$ und $f(x)$ in Metern gemessen wird. Die Breite des Trogs beträgt oben 55 cm und die Länge ist 1.9 m.
a) Berechne, wie viel Wasser in den Trog passt, wenn dieser randvoll gefüllt wird.
b) Berechne, wie viel Wasser in den Trog passt, wenn dieser bis 5 cm unter dem Rand gefüllt wird.
#1234 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Es sind die Exponentialfunktion $f(x)=0.5\cdot 1.65^x$ und das Intervall $[x_1, x_2]=[2.6,5.7]$ gegeben. Es soll anhand dieser Informationen der Flächeninhalt $A$ der in der nachfolgenden (nicht maßstabsgetreuen) Skizze grau markierten Fläche berechnet werden.
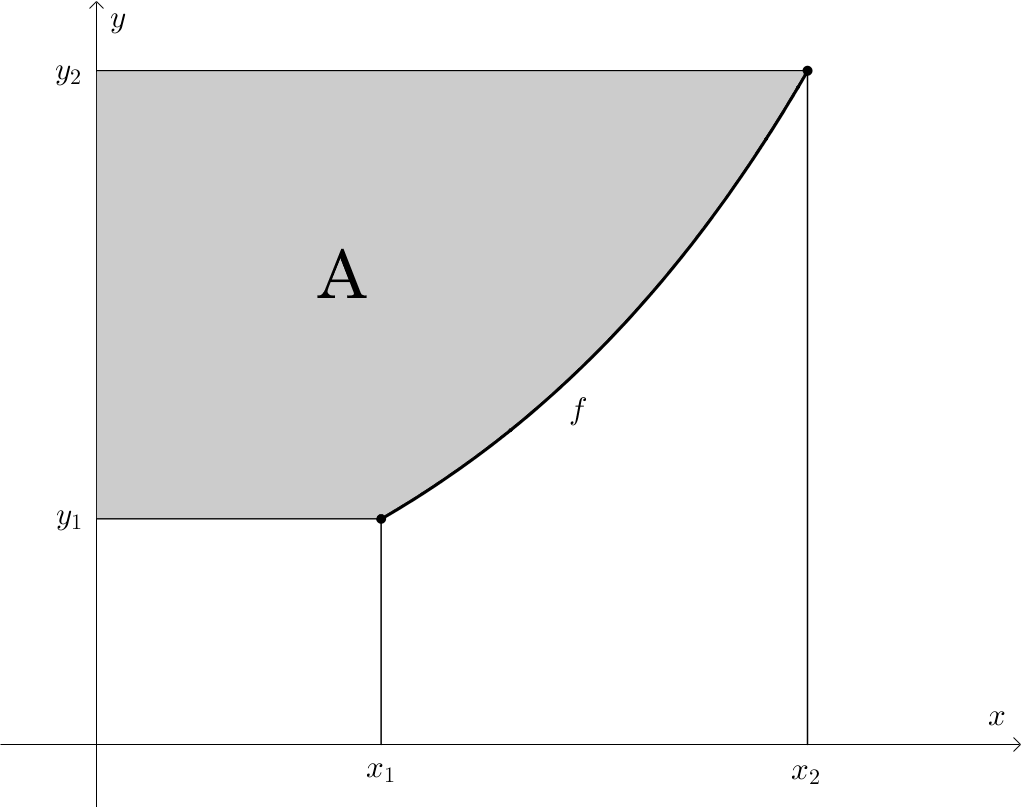
a) Gib das Intervall $[y_1,y_2]$ an.
b) Bestimme die Funktionsgleichung der zugehörigen Umkehrfunktion.
c) Berechne den Flächeninhalt der Fläche $A$.
4. Stammfunktionen grafisch bestimmen
Nachfolgend ist der Funktionsgraph einer Funktion abgebildet.Skizziere im selben Koordinatensystem den Funktionsgraphen einer zugehörigen Stammfunktion.


Nachfolgend ist der Funktionsgraph einer Funktion abgebildet.Skizziere im selben Koordinatensystem den Funktionsgraphen einer zugehörigen Stammfunktion.


#680 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Unten ist der Graph der Funktion $f$ im Intervall $[0;3]$ abgebildet. Zeichne den Graphen einer möglichen Stammfunktion von $f$.
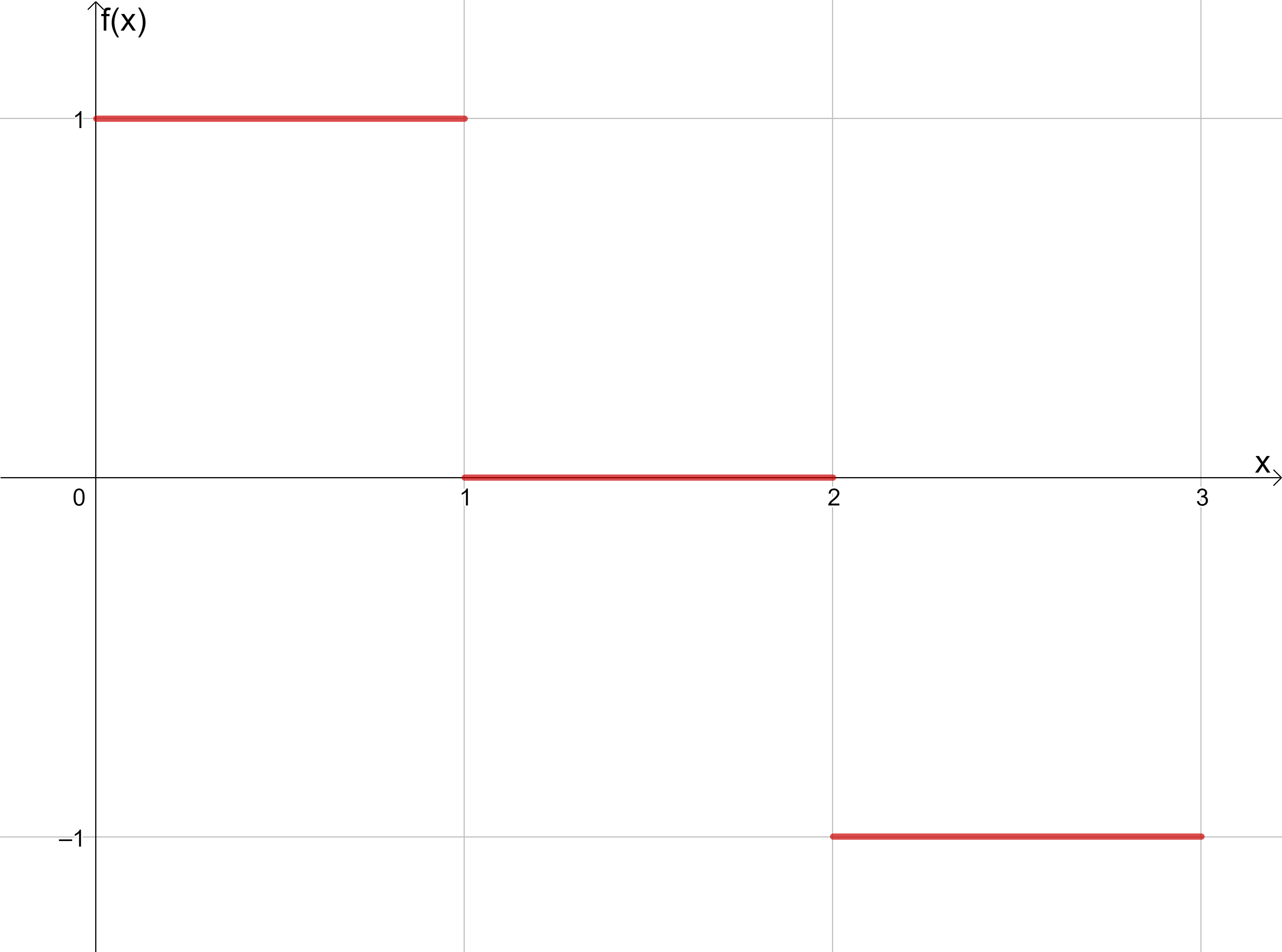
5. Rotationskörper
Lässt man den Graphen der Funktion $r(x)=2.3+1.8\cdot \sqrt[4]{x}$ im Intervall $[0,29]$ um die $x$-Achse rotieren, so entsteht eine Vase, deren Boden sich bei $x=0$ befindet. Sowohl $x$ als auch $r(x)$ sind in Zentimetern gemessen.
a) Berechne die Standfläche der Vase.
b) Berechne das Volumen der Vase.
c) Berechne den Öffnungsdurchmesser der Vase.
d) Berechne die Füllhöhe, bei welcher 70 % des Gesamtvolumens erreicht sind.
#1237 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Die Innenoberfläche des Kühlturms eines Kernkraftwerks kann man erhalten, indem man den Funktionsgraph der Funktion $f(x)=\frac{1}{0.00086x-0.025}-47$ um die $y$-Achse rotieren lässt. Dabei sind $x$ und $f(x)$ in Metern gemessen. Der Boden befindet sich bei $y=0$. Die Höhe des Turms beträgt 196 m.
a) Berechne durch handschriftliche Rechnung den sogenannten Mündungsdurchmesser, also den Durchmesser am oberen Ende des Kühlturms.
b) Bestimme durch handschriftliche Rechnung die Umkehrfunktion $f^{-1}(y)$. Vermeide Doppelbrüche im Ergebnis!
c) Berechne das Volumen im Inneren des Kühltums.
d) Die Wanddicke beträgt 40 cm. Es soll die für den Bau notwendige Betonmasse (Dichte: 2.31 t/m³) berechnet werden. Gehe dazu folgendermaßen vor: Das Innenvolumen ist aus Aufgabe c) bekannt. Das Außenvolumen kann analog dazu erhalten werden, jedoch muss die Wanddicke zur Funktion $f^{-1}(y)$ addiert werden (Einheiten beachten). Das Volumen des benötigten Betons entspricht der Differenz. Daraus kann schließlich die Masse berechnet werden.
6. Uneigentliche Integrale
#636 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Gegeben ist die Funktion $f:[1,\infty)\to\mathbb{R}$ mit der Funktionsgleichung $f(x)=\frac{1}{x}$. Der Funktionsgraph soll um die x-Achse rotieren. Der dadurch entstehende Körper wird als „Gabriels Horn“ bezeichnet.
a) Berechne durch handschriftliche Rechnung das Volumen dieses Körpers.
b) Berechne mit einem geeigneten Computerprogramm die Mantelfläche dieses Körpers.
c) Vergleiche die Ergebnisse und beschreibe, was daran widersprüchlich erscheint und wie man diesen Widerspruch auflösen könnte. Recherchiere gegebenenfalls im Internet.
#836 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Gegeben sind die Funktionen $f(x)=\frac{1}{x^2+1}$ und $g(x)=e^{-x^2}$.
a) Skizziere die Funktionsgraphen beider Funktionen und beschreibe deren Unterschiede.
b) Berechne für beide Funktionen jeweils den Flächeninhalt zwischen Funktionsgraph und $x$-Achse im Intervall $(-\infty,\infty)$.
c) Berechne die Volumen der beiden Rotationskörper, welche entstehen, wenn die Funktionsgraphen um die $x$-Achse rotieren.
d) Berechne die Volumen der beiden Rotationskörper, welche entstehen, wenn die Funktionsgraphen um die $y$-Achse rotieren.
e) Was ist bemerkenswert an den Ergebnissen? Versuche eine Begründung dafür zu finden.
#1242 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Gegeben ist die Funktionsgleichung $f(x)=\frac{1.8}{x^4+0.49}$.
a) Berechne den Flächeninhalt zwischen Funktionsgraph und $x$-Achse im Intervall $(-\infty,\infty)$.
b) Berechne das Volumen des Rotationskörpers, welcher entsteht, wenn der Funktionsgraph um die $x$-Achse rotiert.
c) Berechne das Volumen des Rotationskörpers, welcher entsteht, wenn der Funktionsgraph um die $y$-Achse rotiert.
d) Fertige eine Skizze der beiden Rotationskörper an. Beschrifte die Skizzen so, dass erkennbar ist, welcher Körper durch Rotation um die $x$-Achse bzw. die $y$-Achse entstanden ist.
7. Vermischte Aufgaben
An einem bestimmten Tag wurde die Dosisleistung im Inneren eines Atomkraftwerks durch folgende Funktion beschrieben:
$$f(t)=8.5\cdot 10^{-4}\cdot t^3-3.55\cdot 10^{-2}\cdot t^2+0.361\cdot t+1.21$$
Dabei ist $t$ die Zeit in Stunden, wobei $t=0$ für 0:00 Uhr und $t=24$ für 24:00 Uhr steht. Der Funktionswert $f(t)$ gibt die momentane Dosisleistung in Mikrosievert pro Stunde (µSv/h) an.
a) Ein Arbeiter befand sich von 14 Uhr bis 21 Uhr im Atomkraftwerk. Berechne, welche Dosis er über diesen Zeitraum hinweg insgesamt aufgenommen hat. Die Dosis ist das bestimmte Integral der Dosisleistung über einen bestimmten Zeitraum hinweg.
b) Zu welcher Uhrzeit war die Dosisleistung an diesem Tag am größten? Gib das Ergebnis im Format HH:MM an (gegebenenfalls inklusive führender Nullen). Für Aufgabe e) ist es außerdem sinnvoll, auch den Maximalwert zu bestimmen.
c) Laut Sicherheitsbestimmungen, darf eine Person pro Tag nur 20 µSv aufnehmen. Jemand begann um 2:30 Uhr im Atomkraftwerk zu arbeiten. Um welche Uhrzeit musste er die Arbeit beenden? Gib das Ergebnis erneut im Format HH:MM an (gegebenenfalls inklusive führender Nullen).
d) Berechne den linearen Mittelwert der Dosisleistung über den gesamten Tag hinweg.
e) Um wie viel Prozent lag die maximale Dosisleistung über der mittleren Dosisleistung?
#228 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Es ist die Funktionsgleichung $u(t)=20\cdot (1-0{,}8^t)$ gegeben.
a) Erstelle eine Formel, mit welcher der lineare Mittelwert dieser Funktion im Intervall $[3;~10]$ berechnet werden kann.
b) Der Graph der Funktion $u$ soll um 3 nach rechts verschoben werden. Bestimme die Funktionsgleichung der verschobenen Funktion $u_2$.
Gegeben ist die Funktion $f(x)=8x-3.4x^2$.
a) Berechne den Flächeninhalt, den der Funktionsgraph zwischen den beiden Nullstellen mit der $x$-Achse einschließt.
b) Berechne, an welcher Stelle sich eine senkrechte Gerade befinden muss, um die Fläche aus a) im Verhältnis 2:1 zu teilen, wobei der linke Teil der größere Teil ist.
c) Berechne, in welcher Höhe sich eine waagrechte Gerade befinden muss, um die Fläche aus a) in zwei gleiche Teile zu teilen.
#637 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Das in Europa, Australien und großen Teilen Asiens verwendete Stromnetz hat eine Frequenz von 50 Hz und eine Scheitelspannung von 325 V. Der zeitliche Spannungsverlauf kann somit durch die Funktion $U(t)=325\cdot \sin(2\pi t\cdot 50)$ beschrieben werden. Die Effektivspannung $\hat U$ ist jene Gleichspannung, die am selben Widerstand pro Periode die gleiche elektrische Energie liefert, wie die betrachtete Wechselspannung. Diese Energie ist proportional zur elektrischen Leistung und somit wiederum proportional zu $U^2$. Berechne die Effektivspannung der gegebenen Wechselspannung.
Schätze den Inhalt der grau dargestellten Fläche möglichst genau.
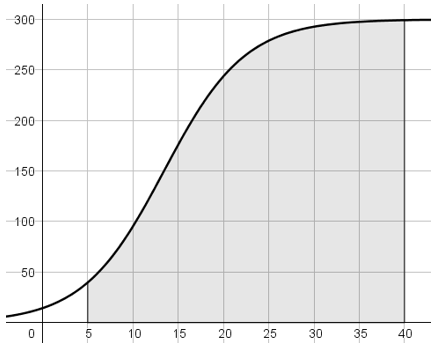

#703 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Nachfolgend ist ein Grundstück abgebildet, dessen obere Begrenzungslinie durch die Funktionsgleichung $f(x)=16+0{,}02x^2$ beschrieben wird.
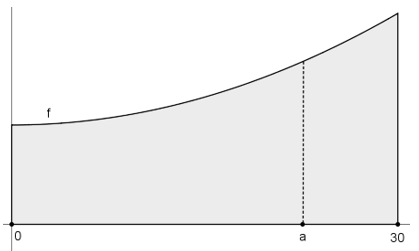
a) Berechne den Flächeninhalt der gesamten grau dargestellten Grundstücksfläche.
b) Das Grundstück soll gemäß der Abbildung so geteilt werden, dass die linke Teilfläche doppelt so groß ist, wie die rechte Teilfläche. Berechne, an welcher Stelle $a$ sich die Teilungsline befinden muss.
#1165 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Von einer Polynomfunktion 3. Grades ist bekannt, dass die zweite Ableitung $p''(x)=5 x-8$ lautet und dass der Funktionsgraph der Funktion $p$ durch die Punkte $(-6 \mid 3)$ und $(5 \mid -4)$ verläuft. Bestimme die zugehörige Funktionsgleichung in der Form $p(x)=ax^3+bx^2+cx+d$ mit einem geeigneten Computerprogramm.
#1198 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Der Querschnitt eines zweispurigen Tunnels wird durch die Funktion $f(x)=4.91-6.6\cdot 10^{-4}\cdot x^6$ beschrieben, wobei $x$ und $f(x)$ in Metern gemessen werden und sich die Straße bei Höhe 0 befindet. Die Gesamtlänge des Tunnels beträgt 513 m.
a) Berechne die Bodenbreite des Tunnels.
b) Ermittle die Gesamtoberfläche der Tunnelwand (nur seitlich und oben, also ohne Straße).
c) Berechne, wie viel Material benötigt wird, wenn pro Quadratmeter 5.1 kg Putz aufgetragen werden.
© 2016 – 2024 MATHE.ZONE