Aufgaben zur Differentialrechnung
Dieser Bereich der Website befindet sich im Umbau.
Betrachten Sie daher auch folgende Arbeitsblätter für mehr Aufgaben zu diesem Thema:
1. Änderungsmaße
Es soll die Funktion f(x)=4.6⋅1.21x im Intervall [5,9] untersucht werden.
a) Berechne die absolute Änderung in diesem Intervall!
b) Berechne die relative Änderung in diesem Intervall!
c) Berechne die mittlere Änderungsrate (den Differenzenquotient) in diesem Intervall!
d) Berechne die lokale Änderungsrate (den Differentialquotient) an der Stelle 5!
2. Ableitungsfunktion
Gegeben ist die Polynomfunktion f(x)=7x4+4x3−7x2+2x−15. Berechne die folgenden Ableitungen:
a) f′(2)
b) f″
c) ~~f'''(2)
Berechne jeweils f'(3.11) der folgenden Funktionen!
a) f(x)=x^3\cdot 2.52^x
b) f(x)=\sqrt[8]{4 x^3}
c) f(x)=\frac{x}{x^2+3.2}
d) f(x)=\sqrt{x^2+8 x+23}
e) f(x)=e^{-(x-2.6)^2}
#1117 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Berechne die ersten vier Ableitungen der folgenden Funktion. Vereinfache so weit wie möglich.
f(x)=1+\frac{1}{2}\cdot x^2\cdot \ln(x)-\frac{x^2}{4}
#1150 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Es ist die Funktionsgleichung einer logistischen Funktion gegeben:
N(t)=\frac{981}{1+20\cdot 0.74^t}
Ermittle die zugehörige Ableitungsfunktion N' und vereinfache diese so weit wie möglich.
#1383 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Es ist die Funktionsgleichung f(x)=e^{-(x-1.6)^2} gegeben. Ermittle die Ableitungsfunktion und vereinfache das Ergebnis so weit wie möglich.
#1384 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Es ist die Funktionsgleichung f(x)=x^5\cdot 1.56^x gegeben. Ermittle die Ableitungsfunktion und vereinfache das Ergebnis so weit wie möglich.
#1385 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Es ist die Funktionsgleichung f(x)=\sqrt[3]{6 x^6} gegeben. Ermittle die Ableitungsfunktion und vereinfache das Ergebnis so weit wie möglich.
#1386 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Es ist die Funktionsgleichung f(x)=\frac{x}{x^2+3.1} gegeben. Ermittle die Ableitungsfunktion und vereinfache das Ergebnis so weit wie möglich.
#1387 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Es ist die Funktionsgleichung f(x)=\sqrt{2x^2+7 x+29} gegeben. Ermittle die Ableitungsfunktion und vereinfache das Ergebnis so weit wie möglich.
3. Hochpunkt, Tiefpunkt, Wendepunkt
Gegeben ist die kubische Funktion f(x)=0.297 x^3-3.66 x^2 + 8 x-1.9. Diese Funktion besitzt einen Hochpunkt, einen Tiefpunkt und einen Wendepunkt. Berechne jeweils beide Koordinaten dieser Punkte!
Es ist die folgende logistische Wachstumsfunktion gegeben:
f(x)=\frac{514}{1+14 \cdot 0.732^x }
a) Berechne die Koordinaten des Wendepunktes! Diese Aufgabe sollte mit Computereinsatz durchgeführt werden.
b) Berechne die maximale Steigung!
Ergänze den Koeffizienten c der kubischen Funktion f(x)=5 x^3+ c\,x^2-8 x+21 so, dass die Funktion an der Stelle 5.4 einen Wendepunkt besitzt.
#322 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Die Koordinaten (\,x_S\mid y_S\,) des Scheitelpunktes der quadratischen Funktion f(x) = ax^2+ bx + c können durch die Formeln x_S=-\frac{b}{2a} und y_S=\frac{4ac-b^2}{4a} berechnet werden. Leite diese Formeln her, indem du die Differentialrechnung verwendest.
#538 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Ermittle die Koordinaten des Tiefpunkts der Funktion f(x)=x^x.
#1382 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Es ist die folgende Funktionsgleichung gegeben:
f(x)= \frac{3 x^2 -2}{4-2 x} +5
a) Ermittle die Ableitungsfunktion von f. Gib einen vollständigen Rechenweg an und vereinfache das Ergebnis so weit wie möglich.
b) Berechne die Koordinaten der Hoch- und Tiefpunkte.
c) Erkläre nachvollziehbar, wie man ohne Computerprogramm herausfinden kann, ob es sich um einen Hochpunkt oder einen Tiefpunkt handelt.
4. Tangente und Sekante
Gegeben ist die Funktionsgleichung f(x)=5\cdot 0.51^x. Bestimme die Gleichung der Tangente t(x)=k\cdot x+d, welche den Graphen von f an der Stelle 5.4 berührt.
5. Steigungswinkel
Es ist die Funktion f(x)=4x^2-3x+22 gegeben. Berechne den Steigungswinkel an der Stelle 3.9 in Grad.
Das Profil der unten abgebildeten Halfpipe wird durch die Funktion f(x)=0.064 \,x^4 beschrieben. Dabei werden x und f(x) in Metern gemessen.
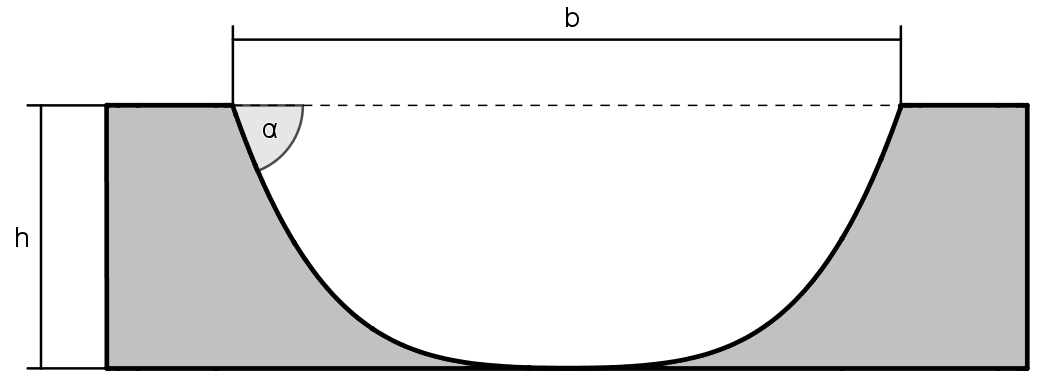

a) Berechne die Breite b der Halfpipe, wenn diese die Höhe h=2.2\,\text{m} besitzen soll.
b) Berechne den maximalen Steigungswinkel \alpha.
Berechne, an welchen Stellen die Funktion f(x)=1.12x^3-5.26x^2+4.93x-3 den Steigungswinkel 55° besitzt.
Es sind die beiden Funktionen f(x)=1.75\cdot 1.186^x und g(x)=2.09\cdot 0.769^x vorgegeben.
a) Berechne beide Koordinaten des Schnittpunkts.
b) Berechne den Betrag des kleineren Schnittwinkels (\,\leq 90^°) der beiden Funktionsgraphen.
6. Grafisches Ableiten
Zeichne den Graphen der zur Funktion g gehörenden Ableitungsfunktion.
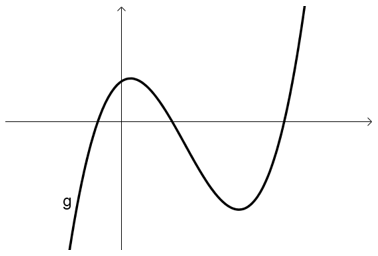

Zeichne den Graphen der zur Funktion f gehörenden Ableitungsfunktion.
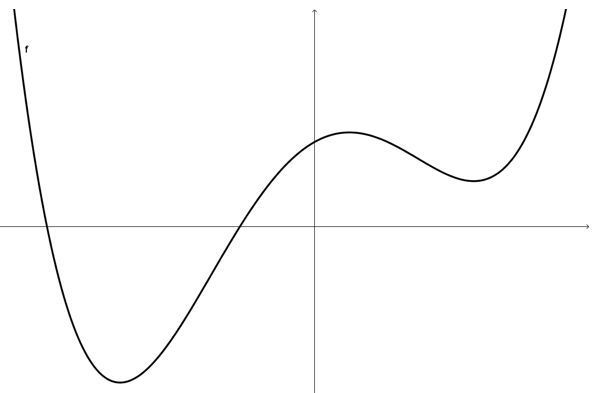

#1444 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Zeichne den Graphen der zur Funktion f gehörenden Ableitungsfunktion.
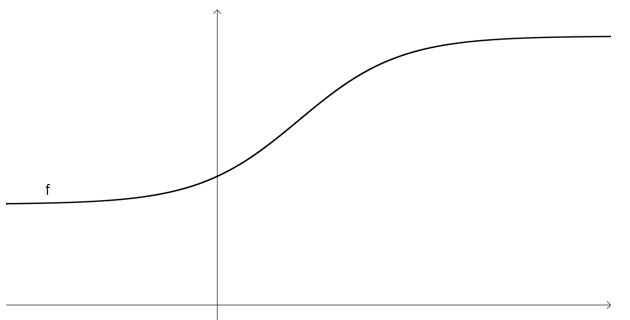
7. Funktionen aufstellen („Steckbriefaufgaben“)
#112 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Nachfolgend ist der Graph einer kubischen Funktion abgebildet.
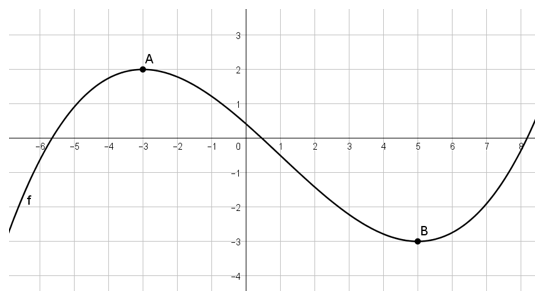
Verwende die Punkte A und B, um die Funktionsgleichung dieser Funktion zu bestimmen.
8. Bewegungsaufgaben
Eine U-Bahn startet zum Zeitpunkt t=0 in Station A und bewegt sich gemäß der Wegfunktion s(t)=-0.0134\,t^3+0.914 \,t^2 zur Station B. Dabei wird t in Sekunden und s(t) in Meter gemessen.
a) Berechne, nach welcher Zeit die U-Bahn in Station B zum Stillstand kommt und welchen Weg sie zwischen den beiden Stationen zurückgelegt hat.
b) Welche Höchstgeschwindigkeit (in km/h) erreicht die U-Bahn bei dieser Fahrt?
c) Berechne die mittlere Geschwindigkeit (in km/h) im Zeitintervall [5.2, 14.9] (gemessen in Sekunden).
d) Berechne die Beschleunigung zum Zeitpunkt des Losfahrens.
Eine U-Bahn benötigt für die Fahrt von einer Station zur nächsten Station 54 Sekunden. Der Abstand der Stationen beträgt 744 m.
a)
Erstelle eine Weg-Zeit-Funktion s in Form einer Polynomfunktion dritten Grades (kubische Funktion). Dabei ist t die Zeit in Sekunden nach dem Losfahren und s(t) der zurückgelegte Weg in Metern. Verwende jeweils den zurückgelegten Weg und die Geschwindigkeit zu den Zeitpunkten t=0 und t=54 s.
b) Berechne gemäß dieser Funktion die Maximalgeschwindigkeit der U-Bahn in der Einheit km/h.
c) Berechne die Beschleunigung zum Zeitpunkt des Losfahrens.
#984 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Für die ersten Sekunden nach dem Absprung gilt für einen Fallschirmspringer näherungsweise die folgende Formel für den freien Fall, da hier der Luftwiderstand noch keine große Rolle spielt:
s(t)=\frac{g}{2}\cdot t^2
Dabei ist t die Zeit nach dem Absprung (gemessen in Sekunden), g=9{,}81\frac{\textrm{m}}{\textrm{s}^2} ist die Gravitationsbeschleunigung und s(t) ist der zurückgelegte Weg (gemessen in Metern).
a) Bestimme die Geschwindigkeitsfunktion des Fallschirmspringers.
b) Berechne die Geschwindigkeit, die der Fallschirmspringer nach 4.4 s hat.
c) Berechne die Durchschnittsgeschwindigkeit, welche er im Zeitintervall [2.3\,\textrm{s};~ 5.4\,\textrm{s}] hat.
d) Wie lange dauert es, bis er 85 m zurückgelegt hat?
Die Höhe einer Feuerwerksrakete wird näherungsweise durch die Funktion h(t)=12.3 t^2 beschrieben, wobei t die Zeit (in Sekunden) nach dem Start und h(t) die zugehörige Höhe (in Metern) sind. Die Rakete explodiert 3.2 s nach dem Start.
a) Berechne, in welcher Höhe die Rakete explodiert.
b) Berechne, welche Geschwindigkeit die Rakete zum Zeitpunkt der Explosion hat.
c) Berechne die Beschleunigung der Rakete.
d) Wie lange dauert es, bis eine Höhe von 39 m erreicht wurde?
e) Nach welcher Zeit wurde eine Geschwindigkeit von 100 km/h erreicht? Achte auf die Einheiten!
9. Vermischte Aufgaben
Während des Beschleunigens eines Fahrzeuges wird dessen zurückgelegter Weg durch die Funktionsgleichung s(t)=0.8 t^2 beschrieben. Dabei wird t in Sekunden und s(t) in Metern gemessen. Berechne die mittlere Geschwindigkeit im Zeitintervall [2\,\mathrm{s}; 5\,\mathrm{s}] in der Einheit km/h.
#994 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Nachfolgend ist der Graph der Funktion f(x)=1+2x^2-\frac{1}{2}\,x^4 abgebildet.
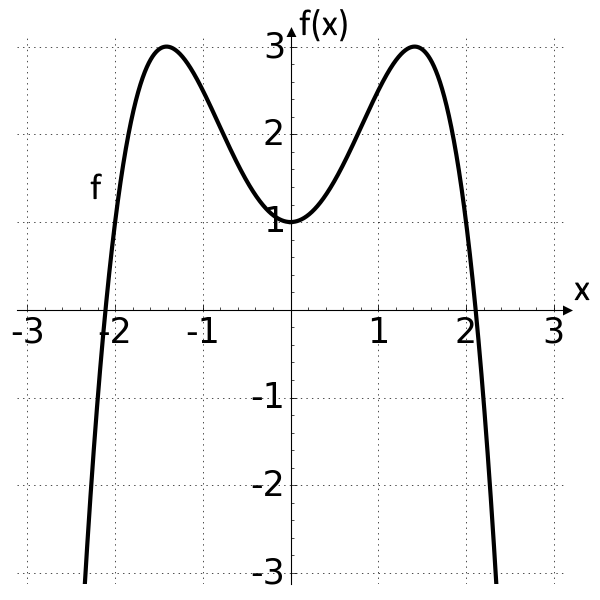
Kreuze jeweils an, ob die Aussage wahr oder falsch ist.
Die Funktion f ist im Intervall [1; 2] streng monoton wachsend.
An der Stelle 1 beträgt der Steigungswinkel des Funktionsgraphen ca. 57,3°.
Für beliebige x gilt f(-x)=f(x).
Die beiden Hochpunkte befinden sich exakt an den Stellen \pm 1{,}5.
Der Graph der ersten Ableitungsfunktion besitzt genau zwei Nullstellen.
Der horizontale Abstand der beiden Wendepunkte beträgt ca. 1,63.
#1092 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Gib an, ob die folgenden Aussagen wahr oder falsch sind.
Die Funktion f(x)=3^x ist durchgehend linksgekrümmt.
Die Funktion f(x)=x^4 hat an der Stelle 0 einen Wendepunkt.
Die Funktion f(x)=2^x\cdot x^2 besitzt genau zwei Wendepunkte.
Die Funktion f(x)=\frac{1}{x^2-6x+10} ist im Intervall [2,5] streng monoton fallend.
Die Funktion f(x)=x^3-6x^2+12x-3 besitzt einen Sattelpunkt.
Die Funktion f(x)=-\frac{5}{16}x^3+\frac{15}{4}x besitzt den Hochpunkt (\, 5 \mid 2 \,).#1322 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Nachfolgend ist ein Funktionsgraph abgebildet, in welchem sechs Punkte markiert wurden.
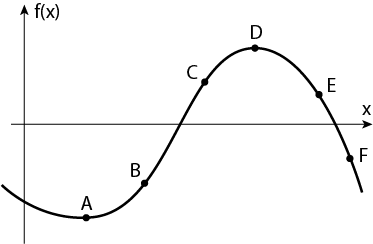
Ordne jeder der folgenden Aussagen den passenden Punkt zu:
▪
f(x)>0,~~ f'(x)<0,~~ f''(x)<0~~~ ▪
f(x)>0,~~ f'(x)=0,~~ f''(x)<0~~~ ▪
f(x)<0,~~ f'(x)>0,~~ f''(x)>0~~~ ▪
f(x)<0,~~ f'(x)=0,~~ f''(x)>0~~~ ▪
f(x)<0,~~ f'(x)<0,~~ f''(x)<0~~~ ▪
f(x)>0,~~ f'(x)>0,~~ f''(x)<0~~~
© 2016 – 2025 MATHE.ZONE