Nachfolgend ist der Graph der Funktion $f(x)=1+2x^2-\frac{1}{2}\,x^4$ abgebildet.

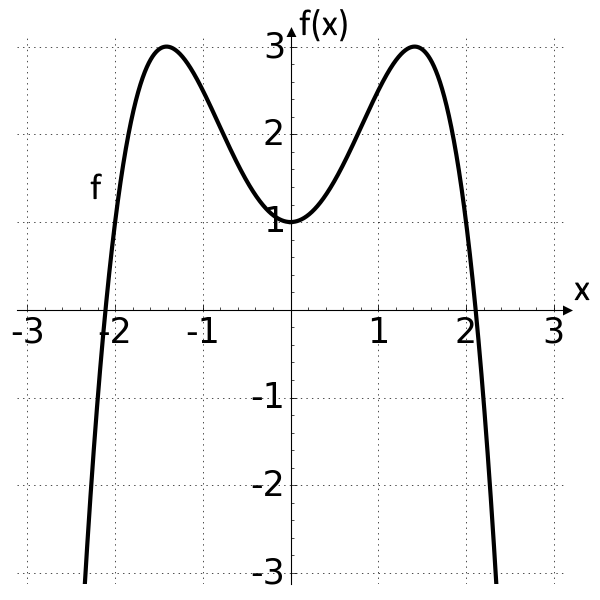
Kreuze jeweils an, ob die Aussage wahr oder falsch ist. wahr falsch Die Funktion $f$ ist im Intervall $[1; 2]$ streng monoton wachsend. wahr falsch An der Stelle 1 beträgt der Steigungswinkel des Funktionsgraphen ca. 57,3°. wahr falsch Für beliebige $x$ gilt $f(-x)=f(x)$. wahr falsch Die beiden Hochpunkte befinden sich exakt an den Stellen $\pm 1{,}5$. wahr falsch Der Graph der ersten Ableitungsfunktion besitzt genau zwei Nullstellen. wahr falsch Der horizontale Abstand der beiden Wendepunkte beträgt ca. 1,63.