Aufgaben zur analytischen Geometrie
Dieser Bereich der Website befindet sich im Umbau.
Betrachten Sie daher auch folgende Arbeitsblätter für mehr Aufgaben zu diesem Thema:
1. Zweidimensionale Vektoren
Bei einem Computerspiel bewegen sich die Charaktere auf einer zweidimensionalen Karte, welche in Längeneinheiten (LE) vermessen wird. Der Charakter des Spielers steht momentan auf Position A(115∣266). Durch Klicken auf den Punkt B(744∣483) bewegt sich die Figur geradlinig mit einer Geschwindigkeit von 37 LE/s von A nach B. Nach 4 Sekunden klickt der Spieler jedoch auf den Punkt C(468∣812). Die Figur bewegt sich nun ausgehend von der aktuellen Position geradlinig und mit gleicher Geschwindigkeit zum Punkt C.
a) An welcher Position X befindet sich die Figur zu jenem Zeitpunkt, an dem der Spieler auf Punkt C klickt.
b) Wie lange benötigte die Figur insgesamt, um von A nach C zu gelangen?
c) Um wie viele Sekunden schneller wäre sie in Punkt C gewesen, wenn der Spieler gleich dort hingeklickt hätte?
d) Stelle die Punkte A,B,C, X und den tatsächlichen Weg der Figur grafisch dar.
Gegeben sind die folgenden drei Vektoren:
\vec a=\binom{8}{5}~~~~\vec b=\binom{5}{-4}~~~~\vec c=\binom{-8}{-7}
Berechne die Ergebnisse der folgenden Rechnungen.
a) ~3\vec a-2\vec b+5\vec c
b) ~3\vec b - 2\cdot (\vec a+4\vec c)
c) ~2\vec c \cdot (3 \vec b - \vec a)
Auf einem sogenannten optischen Tisch (einer zweidimensionalen Station für optische Experimente) wurde eine Ecke dem Punkt (0\mid 0) zugewiesen. Die Tischkanten entsprechen den positiven Halbachsen des Koordinatensystems und sind in x-Richtung 2000 mm und in y-Richtung 1500 mm lang. Im Punkt (1540\mid 340) sollen sich zwei Laserstrahlen treffen. Laser A ist in Punkt (525\mid 150) positioniert. Laser B soll halb so weit vom Zielpunkt entfernt sein wie Laser A und normal auf dessen Strahl stehen.
a) Erstelle eine aussagekräftige und vollständig beschriftete Skizze des Sachverhalts.
b) Bestimme die Position von Laser B.
Das Viereck \mathrm{ABCD} besitzt die Eckpunkte \mathrm{A}(-2 \mid 7), \mathrm{B}(1 \mid 6), \mathrm{C}(6 \mid -5) und \mathrm{D}(-5 \mid -3). Alle Angaben sind in Zentimetern.
a) Stelle das Viereck im Koordinatensystem dar und beschrifte die Skizze.
b) Berechne den Umfang des Vierecks.
c) Berechne den Innenwinkel des Vierecks im Eckpunkt \mathrm{C}.
d) Berechne den Flächeninhalt des Vierecks.
Gegeben sind die folgenden beiden Kraftvektoren (alle Angaben in Newton):
\vec{F}_1=\binom{343}{-467} \hspace{1cm}\text{und}\hspace{1cm} \vec{F}_2=\binom{540}{289}
a) Stelle die beiden Kraftvektoren und den Vektor der resultierenden Kraft grafisch dar und beschrifte alle Vektoren.
b) Berechne den Vektor und den Betrag der resultierenden Kraft.
c) Berechne den Winkel zwischen den beiden Kraftvektoren.
d) Ändere die x-Komponente von \vec{F}_1 so, dass die beiden Kraftvektoren orthogonal sind.
Vom Parallelogramm \mathrm{ABCD} sind die drei Eckpunkte \mathrm{A}(-2 \mid 3.5), \mathrm{B}(3.5 \mid 2) und \mathrm{D}(-3 \mid -4.5) bekannt. Alle Angaben sind in Zentimetern.
a) Stelle das Parallelogramm im Koordinatensystem dar und beschrifte die Skizze.
b) Berechne den fehlenden Eckpunkt C.
c) Berechne den Umfang des Parallelogramms.
d) Berechne den Winkel des Parallelogramms im Punkt A.
e) Berechne den Flächeninhalt des Parallelogramms.
f) Ersetze den Punkt D durch einen neuen Punkt E, sodass die Vektoren \overrightarrow{\mathrm{AB}} und \overrightarrow{\mathrm{AE}} eine Raute aufspannen.
Ein Dreieck besitzt die Eckpunkte \mathrm{A}(-1 \mid 3), \mathrm{B}(4 \mid -5) und \mathrm{C}(-3 \mid -6). Alle Angaben sind in Zentimetern gemessen.
a) Stelle das Dreieck im Koordinatensystem dar und beschrifte die Skizze.
b) Berechne den Umfang des Dreiecks.
c) Berechne den Innenwinkel des Dreiecks im Eckpunkt A.
d) Berechne den Flächeninhalt des Dreiecks.
e) Berechne den Schwerpunkt des Dreiecks.
#1039 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Der Polarstern kann am Nachthimmel durch einen Trick relativ einfach gefunden werden. Zunächst sucht man das Sternbild „Großer Wagen“. Nun zieht man eine Gerade durch die Sterne \alpha und \beta des Sternbilds, auf welcher auch der Polarstern liegt. Der Abstand zwischen \alpha und Polarstern ist ungefähr fünfmal so groß wie jener zwischen \alpha und \beta. In einer Abbildung werden für \alpha die Koordinaten (307\mid244) und für \beta die Koordinaten (288\mid207) abgelesen. Berechne, bei welchen Koordinaten der Polarstern gesucht werden muss.

Koordinaten: [0]
#1388 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Es ist der Vektor \vec a = \binom{-4}{-5} gegeben.
a) Bestimme einen beliebigen Vektor, der normal zum Vektor \vec a ist. Gib auch eine Rechnung an, die zeigt, dass die geforderte Eigenschaft erfüllt ist.
b) Bestimme einen beliebigen Vektor, der parallel zum Vektor \vec a ist. Gib auch eine Rechnung an, die zeigt, dass die geforderte Eigenschaft erfüllt ist.
c) Bestimme einen beliebigen Vektor, der antiparallel zum Vektor \vec a ist. Gib auch eine Rechnung an, die zeigt, dass die geforderte Eigenschaft erfüllt ist.
#1389 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Nachfolgend sind einige Aussagen zum Skalarprodukt aufgelistet. Beweise entweder, dass diese Eigenschaft für zweidimensionale Vektoren allgemein gilt oder widerlege sie durch ein passendes Gegenbeispiel. Beschreibe jeweils verbal, zu welcher Schlussfolgerung du gekommen bist.
a) ~\vec a\cdot \vec b = \vec b\cdot \vec a
b) ~\vec a\cdot (\vec b \cdot \vec c) = (\vec a\cdot \vec b) \cdot \vec c
c) ~\vec a\cdot (\vec b + \vec c) = \vec a\cdot \vec b + \vec a \cdot \vec c
#1392 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Gegeben sind die Punkte \mathrm{A}(-3 \mid -4) und \mathrm{B}(2 \mid -3). Ermittle jeweils den Punkt \mathrm{C} so, dass die vorgegebene Eigenschaft erfüllt ist. Dokumentiere deine Vorgehensweise jeweils nachvollziehbar.
a) Das Dreieck \mathrm{ABC} soll rechtwinklig sein.
b) Das Dreieck \mathrm{ABC} soll gleichschenklig sein.
c) Das Dreieck \mathrm{ABC} soll gleichseitig sein.
#1393 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Bei einer Kindergeburtstagsfeier wird ein Schatz gesucht. Die Kinder erhalten folgende Anweisungen:
▪
Starte beim Punkt (8 m | 22 m). ▪
Gehe 11 m nach Norden und 22 m nach Westen. Benutze dazu den kürzesten Weg zu diesem Punkt. ▪
Drehe dich um 90° nach links und gehe 22 m in diese Richtung. ▪
Drehe dich in Richtung des Startpunkts und gehe zwei Drittel der Strecke bis zum Startpunkt. ▪
Gehe abschließend die Hälfte der bei der letzten Anweisung zurückgelegten Distanz nach Süden.
a) Zeichne die Route möglichst genau in ein Koordinatensystem. Wähle eine passende Skalierung.
b) Lies ab, bei welchen Koordinaten sich der Schatz befindet.
c) Bestimme die Länge der gesamten Route.
#1395 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Nachfolgend sind zwei zweidimensionale Vektoren gegeben. Alle Werte haben die Einheit cm.
\vec a = \begin{pmatrix} 1\\ 6 \end{pmatrix},~~~~~~~ \vec b = \begin{pmatrix} -5\\ -6 \ \end{pmatrix}
a) Berechne die Längen der beiden Vektoren.
b) Berechne den Winkel zwischen den beiden Vektoren.
c) Berechne den Flächeninhalt des Dreiecks, welches von diesen Vektoren aufgespannt wird.
#1441 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Es ist die folgende Abbildung vorgegeben:
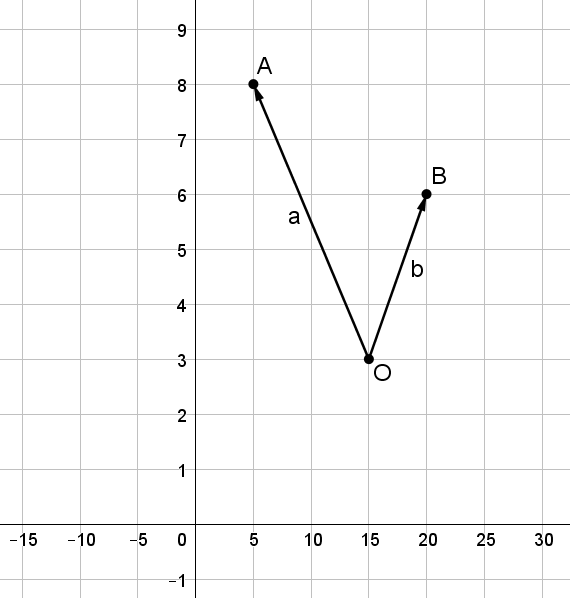
a) Berechne den Winkel zwischen den Vektoren \vec a und \vec b.
b) Erkläre, warum das Ergebnis einem stumpfen Winkel entspricht, obwohl in der Abbildung ein spitzer Winkel erkennbar ist.
2. Dreidimensionale Vektoren
Auf ein Objekt wirken im Schwerpunkt die folgenden drei Kräfte (alle Angaben in Newton):
\vec F_1=\begin{pmatrix} 424 \\ 136 \\ -254 \end{pmatrix} \hspace{7mm} \vec F_2=\begin{pmatrix} 358 \\ -170 \\ -45 \end{pmatrix}\hspace{7mm} \vec F_3=\begin{pmatrix} -608 \\ -430 \\ 169 \end{pmatrix}
a) Berechne die resultierende Kraft \vec F_R, welche auf dieses Objekt wirkt, sowie deren Betrag.
b) Berechne den Winkel, um welchen \vec F_R von der positiven y-Richtung abweicht.
c) Füge eine beliebige vierte Kraft hinzu, sodass das Objekt ausschließlich in y-Richtung beschleunigt wird.
Ein ebenes Dreieck im Raum ist gegeben durch die Eckpunkte A(8 \mid -2 \mid 5), B(-5 \mid 3 \mid 8) und C(7 \mid 8 \mid -6).
a) Berechne den Umfang des Dreiecks.
b) Berechne, welchen Winkel das Dreieck im Eckpunkt A hat.
c) Berechne den Flächeninhalt.
d) Punkt C soll durch einen beliebigen anderen Punkt D ersetzt werden, sodass das Dreieck ABD rechtwinklig ist. Finde nachvollziehbar einen derartigen Punkt und gib dessen Koordinaten an!
Einem bestimmten Computerspiel liegt ein dreidimensionales kartesisches Koordinatensystem zugrunde, welches in Längeneinheiten (LE) vermessen wird. Ein Projektil wurde vom Punkt (455\mid 330\mid 80) abgefeuert, wobei der Punkt (831\mid 680\mid 23) anvisiert wurde. Die Projektilgeschwindigkeit beträgt konstant 560 LE/s. Welche Distanz muss das Projektil zurücklegen und nach welcher Zeit ist das Ziel erreicht?
#1042 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Auf geladene Teilchen, welche sich im elektromagnetischen Feld bewegen, wirkt die sogenannte Lorentzkraft. Die Formel dafür lautet folgendermaßen:
\vec{F}=q\cdot (\vec{E}+\vec{v}\times \vec{B})
Berechne den Kraftvektor und dessen Betrag für die Werte q=1.8, \vec{E}=(-4.2,-4.2,3.1)^\top, \vec{v}=(4.9,2,-4.4)^\top und \vec{B}=(-4.1,3,-3.6)^\top. Alle Größen sind bereits in SI-Einheiten angegeben. Somit ist das Ergebnis in der Einheit Newton. Gib die Komponenten des Vektors durch Schrägstriche getrennt an.
#1390 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Nachfolgend sind einige Aussagen zum Kreuzprodukt aufgelistet. Überprüfe, ob diese Aussagen für die folgenden Vektoren wahr sind. Beschreibe jeweils in einem Antwortsatz, ob die Aussage wahr oder falsch ist.
\vec a = \begin{pmatrix} -3\\ 4\\ 5 \end{pmatrix},~~~~~ \vec b = \begin{pmatrix} 6\\ 3\\ -6 \end{pmatrix} , ~~~~~ \vec c = \begin{pmatrix} 2\\ -6\\ -1 \end{pmatrix}
a) ~\vec a\times\vec b = \vec b\times \vec a
b) ~(\vec a\times \vec b) \cdot \vec c = \vec a \cdot (\vec b \times \vec c)
c) ~(\vec a\times \vec b) \cdot \vec a=0
d) ~\vec a\times (\vec b+ \vec c) = \vec a\times \vec b + \vec a\times \vec c
#1391 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Berechne die folgenden Kreuzprodukte.
a) ~~~\begin{pmatrix} 4 \\ 1 \\ 6 \end{pmatrix} \times \begin{pmatrix} 3 \\ 6 \\ 5 \end{pmatrix}
b) ~~~\begin{pmatrix} -1 \\ 4 \\ 1 \end{pmatrix} \times \begin{pmatrix} 1 \\ -2 \\ 0 \end{pmatrix}
#1394 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Nachfolgend sind zwei dreidimensionale Vektoren gegeben. Alle Werte haben die Einheit cm.
\vec a = \begin{pmatrix} -5\\ 3 \\ -8 \end{pmatrix},~~~~~~~ \vec b = \begin{pmatrix} -7\\ 2 \\ 7 \end{pmatrix}
a) Berechne die Längen der beiden Vektoren.
b) Berechne den Winkel zwischen den beiden Vektoren.
c) Berechne den Flächeninhalt des Dreiecks, welches von diesen Vektoren aufgespannt wird.
3. Vermischte Aufgaben
In der Realität beträgt die Entfernung zwischen zwei Orten A und B 8.5 km. In einer Landkarte werden diese Orte durch den Vektor \binom{5}{8} verbunden. Berechne die „realen“ Koordinaten des Vektors \overrightarrow{\mathrm{AB}} in der Einheit km.
#646 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Es sind die Vektoren \vec u und \vec v mit folgenden Koordinaten gegeben:
\vec u = \binom{u_x}{u_y}~~~~~~~~~~~~~~~\vec v = \binom{-u_y}{u_x}
Zeige allgemein, dass es sich bei diesen Vektoren um Normalvektoren handelt und schreibe eine Begründung.
#734 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Finde zu den folgenden Vektoren jeweils einen Normalvektor.
\vec a=\begin{pmatrix} 7 \\ -1 \end{pmatrix},~~~~~~~~~~\vec b=\begin{pmatrix} 2 \\ -9 \\ 6 \end{pmatrix},~~~~~~~~~~\vec c=\begin{pmatrix} 3 \\ 9 \\ -6 \\ 1 \end{pmatrix}
#1439 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Zwei Schiffe verlassen gleichzeitig den Hafen mit den Koordinaten (0 \mid 0) und bewegen sich geradlinig und mit konstanter Geschwindigkeit. Nach einer Stunde hat Schiff A den Punkt (-27\mid 9) und Schiff B den Punkt (15 \mid 26) erreicht. Alle Abmessungen sind in Kilometern angegeben.
a) Erstelle eine Skizze, in welcher der Hafen sowie die aktuelle Position der Schiffe ersichtlich ist (inkl. Beschriftungen).
b) Berechne den Abstand der beiden Schiffe zum aktuellen Zeitpunkt (also eine Stunde nach Verlassen des Hafens).
c) Berechne die Geschwindigkeit von Schiff A in der Einheit m/s.
d) Berechne den Winkel zwischen den Routen der beiden Schiffe.
© 2016 – 2025 MATHE.ZONE