Aufgaben zu Folgen (allgemein)
Auf dieser Seite befinden sich Aufgaben zu Folgen (allgemein). Jede Aufgabe besitzt eine Nummer, über welche sie durch die Suchfunktion jederzeit wieder aufgerufen werden kann. Dazu muss als Suchbegriff die Aufgabennummer mit einer Raute davor eingegeben werden, also z. B. #123. Die Aufgaben dieser Internetseite werden in jeder Session – also nach jedem Neustart des Webbrowsers oder nach jedem neuen Login – neu generiert. Bei den meisten Aufgaben bedeutet dies, dass sich einzelne Zahlenwerte verändern. Möchte man zu einem späteren Zeitpunkt erneut auf exakt dieselbe Aufgabe zugreifen, so sollte daher ein Screenshot angefertigt werden.
Inhaltsverzeichnis
1. Monotonie
Gegeben ist die Folge $a_n= 687 n^2-4 n^3$. Diese Folge ist zunächst streng monoton wachsend, was sich jedoch ab einem bestimmten Folgenglied ändert. Ab welchem $n$ gilt
$ a_n < a_{n-1} $?
#1061 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Gib an, ob die folgenden Aussagen wahr oder falsch sind.
Eine nach oben unbeschränkte Folge ist immer streng monoton wachsend.
Jede streng monoton wachsende Folge ist nach oben unbeschränkt.
Eine Folge kann zugleich monton wachsend und monoton fallend sein.
Eine nach oben beschränkte Folge ist niemals streng monoton wachsend.
Die Folge mit dem erzeugenden Term $5 + (-1)^n$ ist alternierend.2. Grenzwert
Gegeben ist die folgende Folge:
$$a_n=\frac{14 n^2+5 n+2}{2 n^2+12}$$
a) Bestimme den Grenzwert $a$ dieser Folge!
b) Ab welchem $n$ gilt $|\,a_n-a\,|<0.001$?
Berechne die Grenzwerte der folgenden Folgen!
a) $a_n=6- \frac{17-8 n^3}{8 n^3+4 n^2-11n+13}$
b) $b_n=\left( 1+\frac{4.7}{n} \right)^n$
c) $c_n=1.4+(-2.9)^n\cdot 0.11^{n}$
a) $a_n=6- \frac{17-8 n^3}{8 n^3+4 n^2-11n+13}$
b) $b_n=\left( 1+\frac{4.7}{n} \right)^n$
c) $c_n=1.4+(-2.9)^n\cdot 0.11^{n}$
#1062 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Gib an, ob die folgenden Aussagen wahr oder falsch sind.
Die Zahl $a$ kann Grenzwert einer Folge sein, obwohl kein einziges Folgenglied tatsächlich den Wert $a$ hat.
Wenn unendlich viele Glieder einer Folge den Wert $a$ haben, dann ist $a$ jedenfalls der Grenzwert dieser Folge.
Wenn $a_n$ eine beschränkte Folge ist und die Folge $b_n$ den Grenzwert 5 besitzt, dann ist der Grenzwert der Folge $a_n \cdot b_n$ jedenfalls 5.
Wenn $a_n$ eine beschränkte Folge ist und die Folge $b_n$ den Grenzwert 0 besitzt, dann ist der Grenzwert der Folge $a_n \cdot b_n$ jedenfalls 0.#1443 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Es ist die Folge $a_n=\frac{5 n^2+20}{6 n^2+17}$ gegeben. Berechne, ab welchem $n$ der Abstand zwischen $a_n$ und dem Grenzwert der Folge kleiner als $10^{-5}$ ist.
3. Vermischte Aufgaben
Bestimme das Supremum und das Infimum der folgenden Folge:
$$a_n=7.1\cdot\left( \frac{1}{n^2}-1 \right)^n+2.5$$
Es ist folgende Folge gegeben:
$$a_n=3 \cdot \sin \left( \frac{n\pi}{5} \right)\cdot \frac{n}{n+12}$$
a) Wie viele Häufungspunkte hat diese Folge?
b) Bestimme den Limes superior und den Limes inferior dieser Folge.
#281 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Nachfolgende Abbildung zeigt die ersten drei Glieder einer Folge.
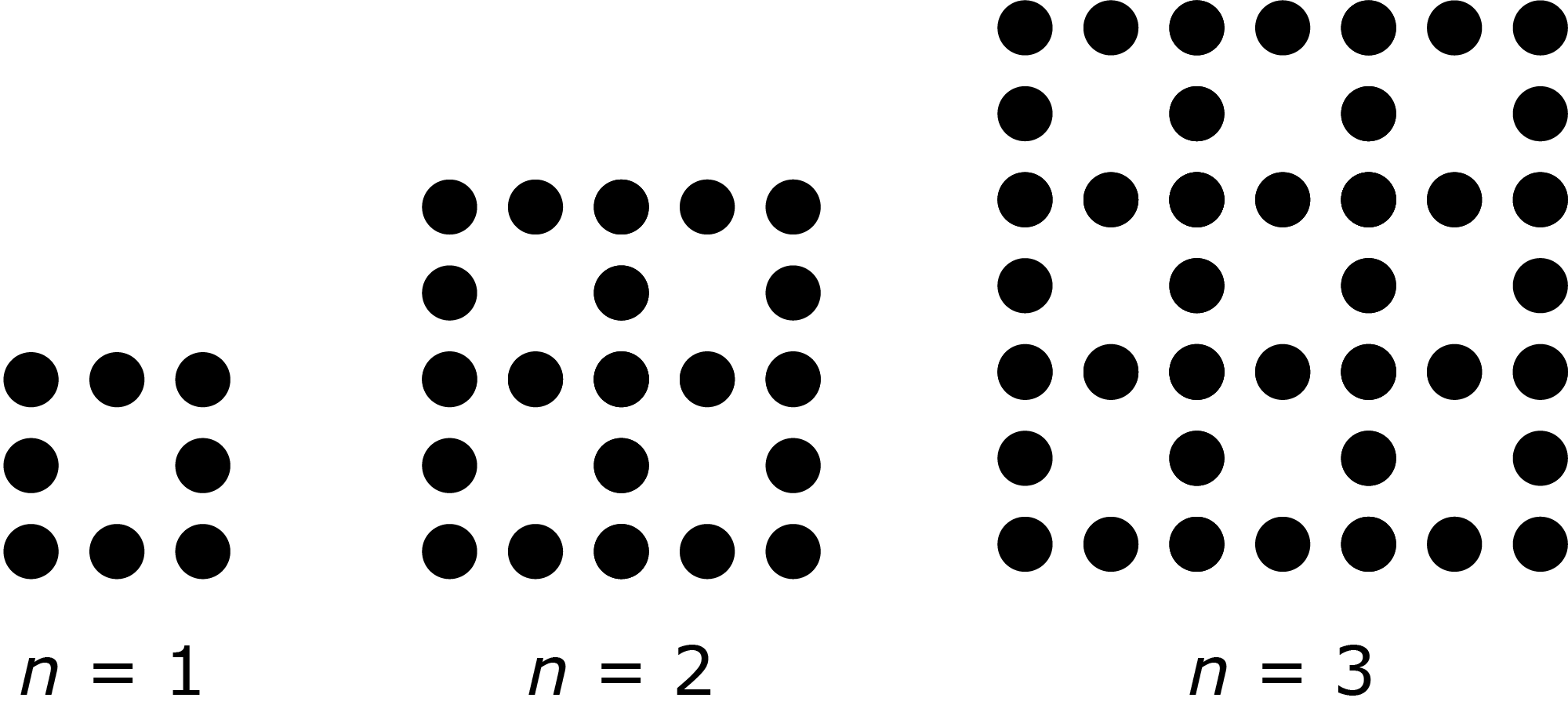
Gib einen Term an, mit dem man die Anzahl der schwarzen Punkte für beliebige Folgenglieder berechnen kann. Vereinfache den Term so weit wie möglich und dokumentiere deine Überlegungen möglichst nachvollziehbar.
Das Collatz-Problem (benannt nach dem deutschen Mathematiker Lothar Collatz) ist eine bisher nicht bewiesene Vermutung, die besagt, dass für eine beliebige positive natürliche Zahl die nachfolgend definierte Folge immer mit dem Zyklus $4, 2, 1, 4, 2, 1, ...$ endet:
▪
Falls das aktuelle Folgenglied gerade ist, dividiere es durch 2. ▪
Falls das aktuelle Folgenglied ungerade ist, multipliziere es mit 3 und addiere 1.
Bestätige diese Vermutung für die Zahl 48, indem du solange alle Folgenglieder aufschreibst, bis die Zahl 1 zum ersten Mal erreicht wurde.
#286 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Nachfolgende Abbildung zeigt die ersten drei Glieder einer Folge.
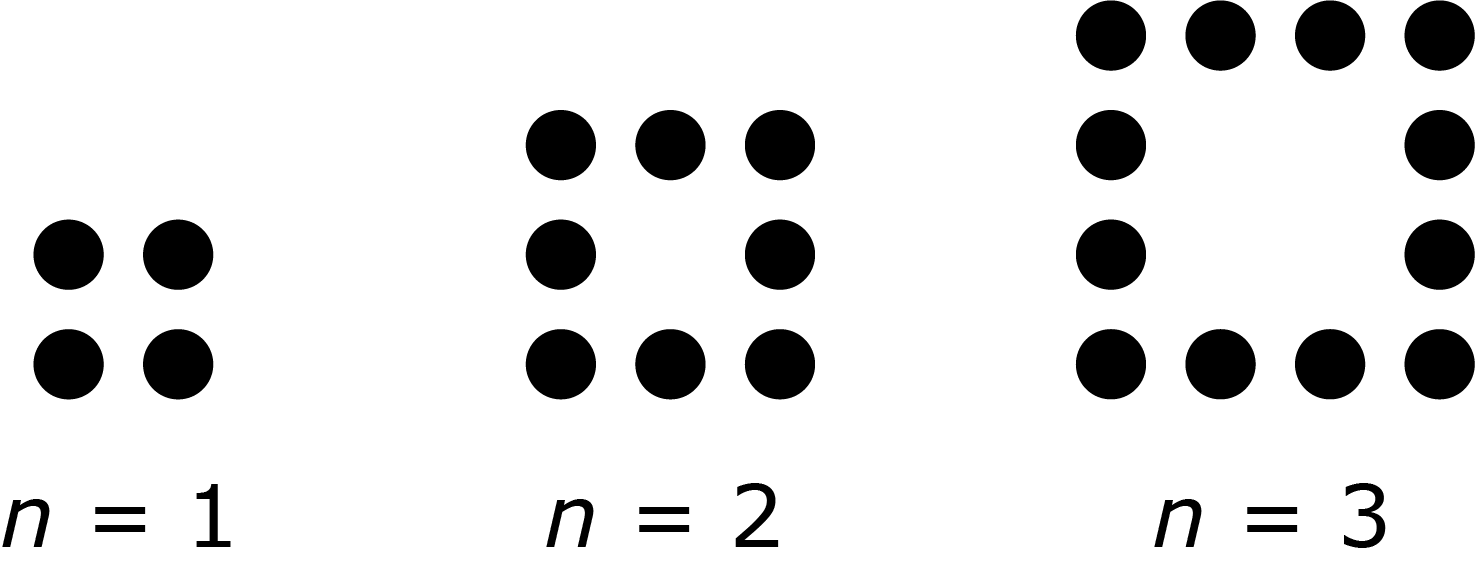
Gib einen Term an, mit dem man die Anzahl der schwarzen Punkte für beliebige Folgenglieder berechnen kann.
#763 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Wird die unten angedeutete Iteration unendlich fortgesetzt, so entsteht das sogenannte Sierpinski-Dreieck.
a) Berechne den Flächeninhalt des Sierpinski-Dreiecks.
b) Berechne den Umfang (die Randlänge) des Sierpinski-Dreiecks.
#1451 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Erstelle jeweils einen Folgenterm, der die vorgegebene Eigenschaft erfüllt. Verwende dazu die Variable $n$.
a) Die Folge soll beschränkt sein, jedoch keinen Grenzwert besitzen.
b) Die Folge soll streng monoton steigend sein und den Grenzwert 6 besitzen.
c) Die Folge alternierend und divergent sein.
Möglichkeiten zur Unterstützung
© 2016 – 2024 MATHE.ZONE