Komplexe Zahlen in Polarkoordinaten
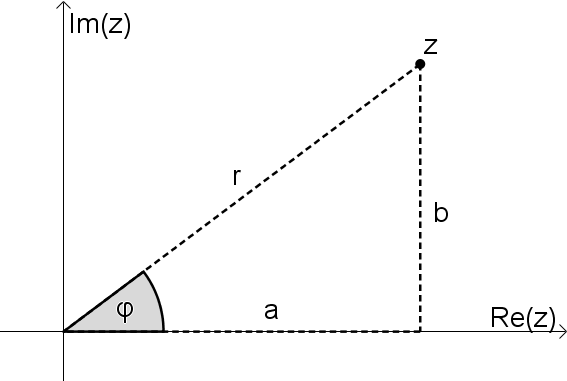
Eine komplexe Zahl kann nicht nur durch ihren Real- und Imaginärteil beschrieben werden, sondern auch durch den Abstand r vom Ursprung (Betrag) und den Winkel φ, den sie mit der Realachse einschließt (gemessen in Radiant, gegen den Uhrzeigersinn). Es gilt folgender Zusammenhang:
a+b⋅i=r⋅eφ⋅i
Hier wird zur eindeutigen Darstellung meistens −π<φ≤π festgelegt. Man bezeichnet die Koordinaten r und φ als Polarkoordinaten. In diesem Zusammenhang wird r auch als Radius und φ als Argument der komplexen Zahl bezeichnet. Für letzteres verwendet man auch die Schreibweise arg(z).
Sofern dies nicht explizit anders angegeben ist, wird im Zusammenhang mit komplexen Zahlen ausschließlich das Bogenmaß (also die Winkeleinheit rad) verwendet.

Umrechnung von kartesischen Koordinaten in Polarkoordinaten
Ist eine komplexe Zahl in der Form a+b⋅i gegeben, so gelten die folgenden Formeln zur Berechnung von r und φ:
r=√a2+b2
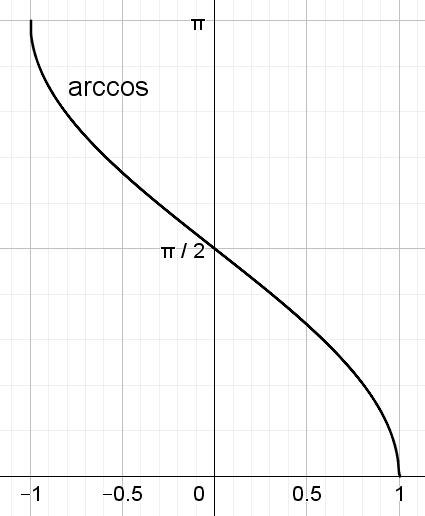
φ={arccos(ar),b≥0−arccos(ar),b<0
Begründung
Es existiert auch eine andere Formel für φ, welche anstelle des arccos den arctan verwendet. Diese Formel ist jedoch weitaus komplizierter anzuwenden, da mehr als zwei Fälle zu berücksichtigen sind bzw. die Ergebnisse noch umgerechnet werden müssen. Daher ist die oben genannte Formel definitiv zu bevorzugen.
Beispiel 1
Es soll die Zahl z=−4−3i in Polarform umgerechnet werden. Durch Einsetzen in die obigen Formeln erhält man die nachfolgenden Resultate. Weil b=−3 negativ ist, verwendet man φ=−arccos(ar).
r=√(−4)2+(−3)2=√25=5
φ=−arccos(−45)≈−2,4981
Das Ergebnis lautet somit z≈5⋅e−2,4981⋅i.
Aufgabe 1
Löse die folgenden Aufgabe: 17@komplexe-zahlen, 13@komplexe-zahlen
Aufgabe 2
Löse von Aufgabe 13 des folgenden Arbeitsblattes die 1. und die 4. Zeile der Tabelle und vergleiche mit den Lösungen auf Seite 3:
|
data/arbeitsblaetter/komplexe-zahlen.pdf
|
Umrechnung von Polarkoordinaten in kartesische Koordinaten
Für die Umrechnung von Polarkoordinaten in kartesische Koordinaten werden folgende Formeln verwendet:
a=r⋅cos(φ)
b=r⋅sin(φ)
Herleitung
Beispiel 2
Es soll die Zahl z=3⋅e2,1⋅i in die kartesiche Form umgerechnet werden. Durch Einsetzen in die Formeln erhält man
a=3⋅cos(2,1)≈−1,51 und b=3⋅sin(2,1)≈2,59. Das Ergebnis lautet daher z≈−1,51+2,59i.
Aufgabe 3
Löse die folgende Aufgabe: 14@komplexe-zahlen
Aufgabe 4
Löse von Aufgabe 13 des folgenden Arbeitsblattes die 3. und die 6. Zeile der Tabelle und vergleiche mit den Lösungen auf Seite 3:
|
data/arbeitsblaetter/komplexe-zahlen.pdf
|
Feedback
Wie hilfreich war dieses Kapitel für dich?
© 2016 – 2025 MATHE.ZONE