Kurse
In dieser Lektion wird darauf eingegangen, welche Zusammenhänge zwischen Exponentialfunktionen und linearen Funktionen bestehen und wodurch sie sich unterscheiden.
1. Wachstumsverhalten
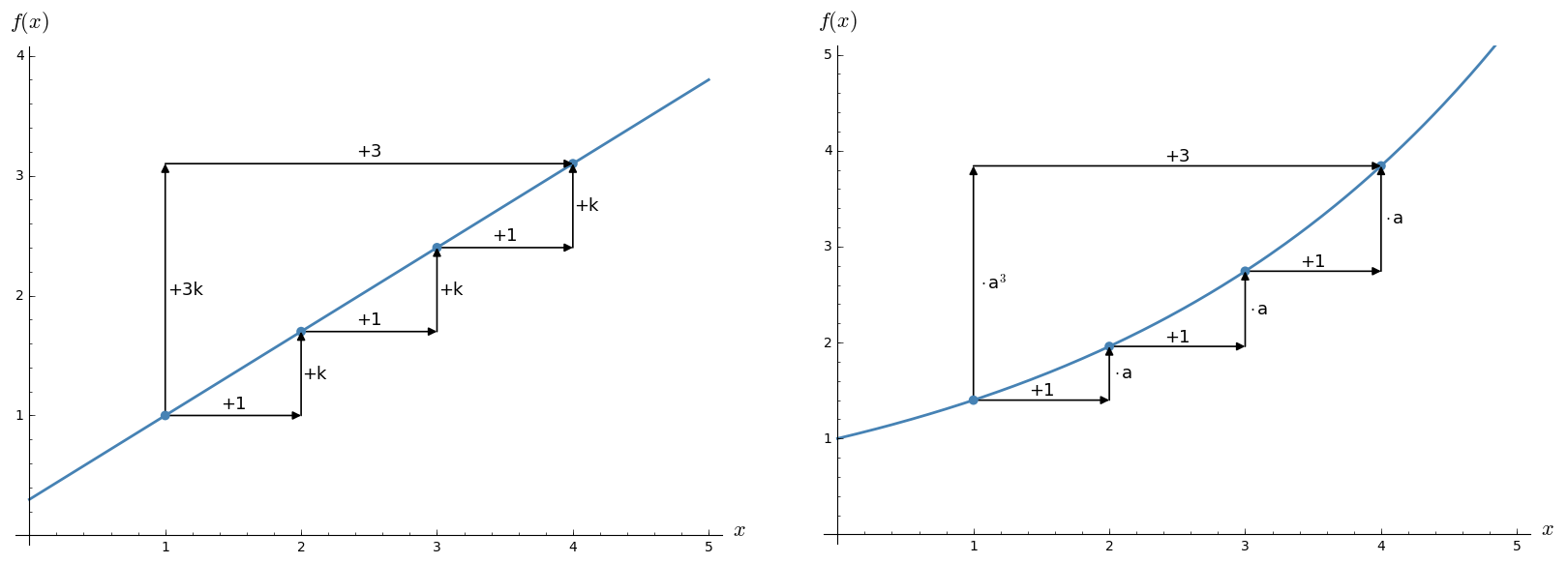
Bei gleichen horizontalen Abständen haben die Funktionswerte einer linearen Funktion immer den gleichen absoluten Zuwachs. Das heißt, zum bestehenden Funktionswert wird immer die gleiche Zahl addiert. Bei Exponentialfunktionen ist hingegen der relative Zuwachs konstant. Das bedeutet, dass hier immer mit demselben Faktor multipliziert wird. Der Zusammenhang wird durch folgende Abbildung graphisch dargestellt. Links
befindet sich eine lineare Funktion, rechts eine Exponentialfunktion.

2. Passenden Funktionstyp wählen
Eine lineare Funktion erkennt man daran, dass sich der Funktionswert stets um einen fixen Zahlenwert ändert. Typische Formulierungen sind beispielsweise folgende:
- Die Bevölkerung wächst jährlich um 3500 Einwohner.
- Die Kosten betragen 200 € pro 50 kg.
- Die Pflanze wächst pro Monat um 8 cm.
- Die Umfragewerte steigen pro Woche um 2 Prozentpunkte.
- Der Wasserstand sinkt pro Stunde um 4,5 cm.
- Die Bevölkerung wächst jährlich um 1,2 %.
- Die Verkaufzahlen verdoppeln sich alle 5 Wochen.
- Die Wirkstoffkonzentration sinkt pro Stunde um 20 %.
- Die Strahlungsintensität halbiert sich alle 2,8 Tage.
- Das Kapital wächst pro Monat um 0,15 %.
Aufgabe 1
3. Funktionstyp anhand einer Wertetabelle erkennen
Bei linearen Funktionen muss die Steigung zwischen allen Punkten gleich sein. Für die beiden Punkte $(x_1\mid y_1)$ und $(x_2\mid y_2)$ wird die Steigung durch den Differenzenquotient $\frac{y_2-y_1}{x_2-x_1}$ berechnet.
Bei Exponentialfunktionen muss der Änderungsfaktor zwischen allen Punkten gleich sein. Dieser wird mittels $\sqrt[x_2-x_1]{\frac{y_2}{y_1} }$ berechnet.
Falls keine der beiden Eigenschaften für alle Punkte erfüllt ist, so handelt es sich weder um einen linearen noch um einen exponentiellen Zusammenhang.
Beispiel 1
Es ist folgende Wertetabelle gegeben:
Es soll überprüft werden, ob einer der beiden Zusammenhänge (linear oder exponentiell) vorliegt. Falls ja, sollen die fehlenden Werte entsprechend ergänzt werden.
Für die Steigungen erhält man folgende Resultate:
$$ \frac{9{,}6 - 2{,}4}{4-2} = 3{,}6$$
$$ \frac{19{,}2 - 9{,}6}{5-4} = 9{,}6$$
Diese Werte sind offensichtlich nicht gleich und daher handelt es sich um keinen linearen Zusammenhang.
Für die Änderungsfaktoren erhält man folgende Resultate:
$$ \sqrt[4-2]{\frac{9{,}6}{2{,}4}} =\sqrt[2]{4} =2$$
$$ \sqrt[5-4]{\frac{19{,}2}{9{,}6}} = 2$$
Da diese Werte gleich sind, entspricht die Tabelle einem exponentiellen Zusammenhang.
Den gesuchten Wert an der Stelle 8 erhält man, indem man 19,2 mit $2^3$ multipliziert. Der Exponent 3 entspricht dem Abstand zwischen dem $x$-Wert 5 und dem $x$-Wert 8. Man erhält $19{,}2\cdot 2^3=153{,}6$.
Den gesuchten Wert an der Stelle $-2$ erhält man, indem man 2,4 mit $2^{-4}$ multipliziert bzw. durch $2^4$ dividiert. Der Exponent $-4$ entspricht dem Abstand zwischen dem $x$-Wert 2 und dem $x$-Wert $-2$ und das negative Vorzeichen folgt daraus, dass der die gesuchte Stelle $-2$ links von der bekannten Stelle 2 liegt. Man erhält $2{,}4\cdot 2^{-4}=0{,}15$.
| $x$ | 2 | 4 | 5 | 8 | $-2$ |
| $y$ | 2,4 | 9,6 | 19,2 | ? | ? |
Beispiel 2
Es ist folgende Wertetabelle gegeben:
Es soll überprüft werden, ob einer der beiden Zusammenhänge (linear oder exponentiell) vorliegt. Falls ja, sollen die fehlenden Werte entsprechend ergänzt werden.
Für die Steigungen erhält man folgende Resultate:
$$ \frac{6 - 3}{3-1} = 1{,}5$$
$$ \frac{12-6}{8-3} = 1{,}2$$
Diese Werte sind offensichtlich nicht gleich und daher handelt es sich um keinen linearen Zusammenhang.
Für die Änderungsfaktoren erhält man folgende Resultate:
$$ \sqrt[3-1]{\frac{6}{3}} = \sqrt[2]{2} \approx 1{,}414$$
$$ \sqrt[8-3]{\frac{12}{6}} = \sqrt[5]{2} \approx 1{,}149$$
Auch diese Werte sind offensichtlich nicht gleich und daher handelt es sich auch um keinen exponentiellen Zusammenhang.
Da keiner der beiden Zusammenhänge vorliegt, können auch die gesuchten Werte nicht bestimmt werden.
| $x$ | 1 | 3 | 8 | 10 | $-3$ |
| $y$ | 3 | 6 | 12 | ? | ? |
Beispiel 3
Es ist folgende Wertetabelle gegeben:
Es soll überprüft werden, ob einer der beiden Zusammenhänge (linear oder exponentiell) vorliegt. Falls ja, sollen die fehlenden Werte entsprechend ergänzt werden.
Für die Steigungen erhält man folgende Resultate:
$$ \frac{6 - 7{,}4}{5-3} = -0{,}7$$
$$ \frac{3{,}9 - 6}{8-5} = -0{,}7$$
Diese Werte sind gleich und daher handelt es sich um einen linearen Zusammenhang. Die Überprüfung des exponentiellen Zusammenhangs ist daher hinfällig.
Den gesuchten Wert an der Stelle 10 erhält man, indem man zum Wert an der Stelle 8 zweimal die Steigung addiert: $3{,}9 + 2\cdot (-0{,}7) =2{,}5$.
Den gesuchten Wert an der Stelle $-1$ erhält man, indem man vom Wert an der Stelle 3 viermal die Steigung subtrahiert: $7{,}4 - 4\cdot (-0{,}7) =10{,}2$.
| $x$ | 3 | 5 | 8 | 10 | $-1$ |
| $y$ | 7,4 | 6 | 3,9 | ? | ? |
Aufgabe 2
Überprüfe nachvollziehbar, welcher Zusammenhang vorliegt und ergänze die fehlenden Werte der nachfolgenden Tabelle.
Lösungen:
ausklappen
| $x$ | $-5$ | $-2$ | $1$ | $7$ | $12$ |
| $y$ | $-7{,}75$ | $-5{,}65$ | $-3{,}55$ |
Aufgabe 3
Überprüfe nachvollziehbar, welcher Zusammenhang vorliegt und ergänze die fehlenden Werte der nachfolgenden Tabelle.
Lösungen:
ausklappen
| $x$ | $-3$ | $-1$ | $2$ | $4$ | $5$ |
| $y$ | 320 | 5 | 0,078125 |
Aufgabe 4
Löse die folgende Aufgabe: #572
4. Weitere Aufgaben
Aufgabe 5
© 2016 – 2024 MATHE.ZONE