Bei der Produktion einer Ware treten drei voneinander unabhängige Fehler mit den Wahrscheinlichkeiten 8.4 %, 6.2 % und 1.5 % auf. a) Wie groß ist die Wahrscheinlichkeit, dass kein Fehler auftritt? b) Wie groß ist die Wahrscheinlichkeit, dass genau ein Fehler auftritt?

Die Wahrscheinlichkeit, dass man bei einem bestimmten Glücksspiel bei insgesamt 3 Versuchen mindestens einmal gewinnt, beträgt laut Betreiber 68 %. a) Wie groß ist die Wahrscheinlichkeit, dass man bei 3 aufeinanderfolgenden Versuchen immer verliert? b) Mit welcher Wahrscheinlichkeit gewinnt man, wenn man nur ein einziges Mal teilnimmt?

In einem Topf befinden sich 10 rote, 6 blaue und 10 gelbe Kugeln. Es werden zwei zufällige Kugeln gezogen (ohne Zurücklegen). a) Wie groß ist die Wahrscheinlichkeit, keine rote Kugel zu ziehen? b) Wie groß ist die Wahrscheinlichkeit, mindestens eine gelbe Kugel zu ziehen? c) Wie groß ist die Wahrscheinlichkeit, genau eine gelbe und eine blaue Kugel zu ziehen?

Bei einem bestimmten Glücksspiel liegt die Gewinnwahrscheinlichkeit für eine einzelne Teilnahme konstant bei 5.2 %. Clemens nimmt 13-mal an diesem Glücksspiel teil. a) Wie groß ist die Wahrscheinlichkeit, dass er genau einmal gewinnt? b) Wie groß ist die Wahrscheinlichkeit, dass er mehr als einmal gewinnt? c) Wie oft müsste er mindestens teilnehmen, um mit einer Wahrscheinlichkeit von mindestens 90 % mindestens einmal zu gewinnen?

Für diese Aufgabe wird angenommen, dass die Wahrscheinlichkeit, an einem bestimmten Wochentag geboren zu werden, für alle Wochentage gleich ist. a) Berechne die Wahrscheinlichkeit, dass zwei zufällig ausgewählte Personen am selben Wochentag geboren sind. Gib das Ergebnis als Bruch an! b) Berechne die Wahrscheinlichkeit, dass zwei zufällig ausgewählte Personen am Mittwoch geboren sind. Gib das Ergebnis als Bruch an!

Eine Maschine wird von zwei voneinander unabhängigen Systemen kontrolliert. System A meldet im Störfall eine Störung mit einer Wahrscheinlichkeit von 81.3 %. System B meldet im Störfall eine Störung mit einer Wahrscheinlichkeit von 93.5 %. Wie groß ist die Wahrscheinlichkeit, dass bei einer Störung mindestens ein System Alarm schlägt?

Jemand trifft das Triple-20-Feld mit einem einzigen Dart mit einer Wahrscheinlichkeit von 14.1 %. Wie groß ist die Wahrscheinlichkeit, dass er bei der nächsten Aufnahme (drei geworfene Darts) eine 180 erzielt, also mit allen drei Darts das Triple-20-Feld trifft? Gehe davon aus, dass die drei Würfe unabhängig voneinander sind (auch wenn dies nicht ganz der Realität entspricht, da beispielsweise die späteren Würfe blockiert werden könnten).

In einem Topf befinden sich 7 Marillenknödel und 11 Zwetschkenknödel, welche optisch nicht unterscheidbar sind. Claudia nimmt sich zwei Knödel. Wie groß ist die Wahrscheinlichkeit, dass sie mindestens ein Zwetschkenknödel am Teller hat?

Es werden drei faire sechsseitige Würfel geworfen. a) Bestimme die Wahrscheinlichkeit, dass alle drei Würfel dieselbe Augenzahl zeigen. b) Bestimme die Wahrscheinlichkeit, dass die Augensumme der drei Würfel mindestens 16 beträgt. c) Bestimme die Wahrscheinlichkeit, dass mindestens ein Würfel die Augenzahl 6 zeigt.

Es werden zwei Münzen geworfen. a) Bestimme die Wahrscheinlichkeit, dass beide Münzen „Kopf“ zeigen. b) Bestimme die Wahrscheinlichkeit, dass mindestens eine Münze „Zahl“ zeigt.

Beim „Mensch ärgere Dich nicht“ muss eine Sechs gewürfelt werden, um eine neue Figur ins Spiel zu bringen. Hat man gar keine Figur im Spiel, so hat man pro Runde drei Würfe, um die benötigte Sechs zu werfen. Berechne die Wahrscheinlichkeit, mit welcher in einer bestimmten Runde der benötigte Sechser geworfen wird.

Eine Analyse hat ergeben, dass 1.7 % aller Fahrgäste keinen gültigen Fahrschein besitzen. Es soll berechnet werden, wie viele Fahrgäste mindestens kontrolliert werden müssen, um mit einer Wahrscheinlichkeit von mindestens 70 % zumindest einen „Schwarzfahrer“ zu erwischen. a) Erstelle eine Gleichung, mit der diese Anzahl berechnet werden kann. b) Berechne die Mindestanzahl.

Bei einer Tombola gibt es 230 Lose. Davon sind 21 Gewinne. Jemand kauft zwei Lose. a) Erstelle ein beschriftetes Baumdiagramm für die beiden Ziehungen. Verwende die Ereignisse „Gewinn“ und „kein Gewinn“, b) Berechne die Wahrscheinlichkeit, dass die Person mindestens einen Gewinn hat.

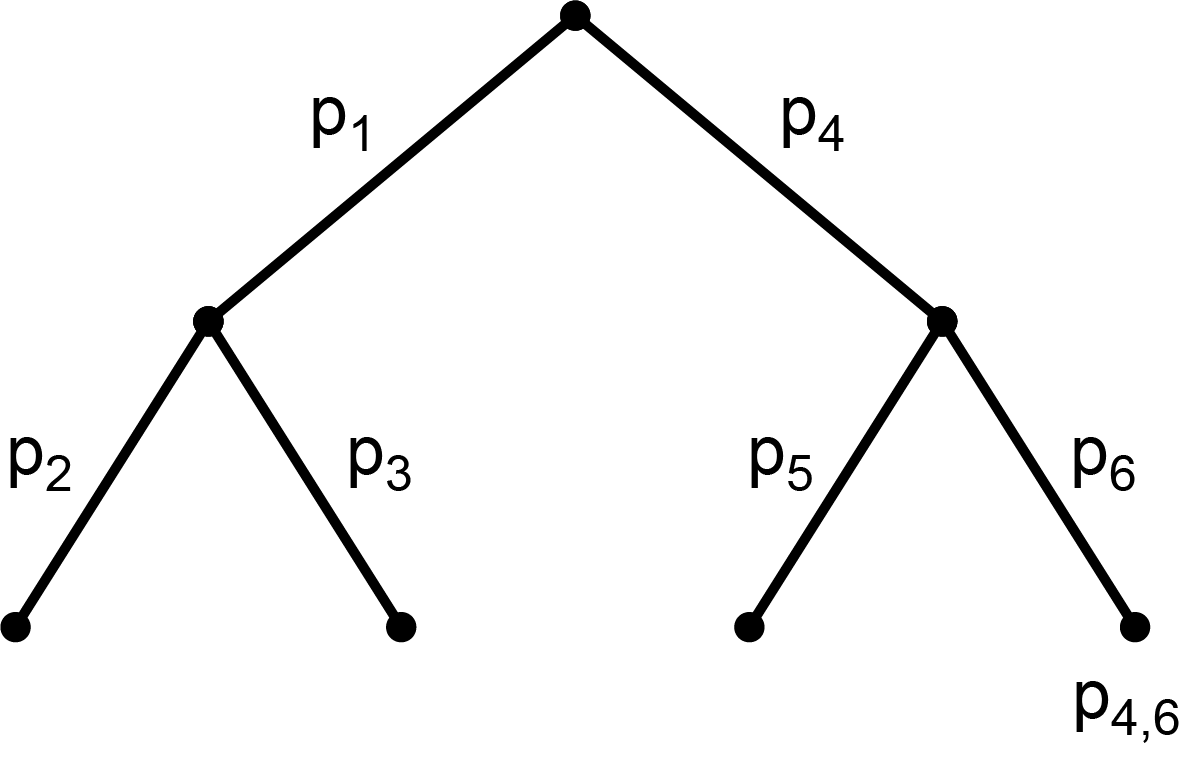
Aus dem nachfolgend abgebildeten Baumdiagramm sind die Werte $p_1=56\,\%$, $p_2=35\,\%$ und $p_{4,6}=24\,\%$ bekannt. Berechne mit dieser Information die Wahrscheinlichkeiten $p_3$, $p_4$, $p_5$ und $p_6$.

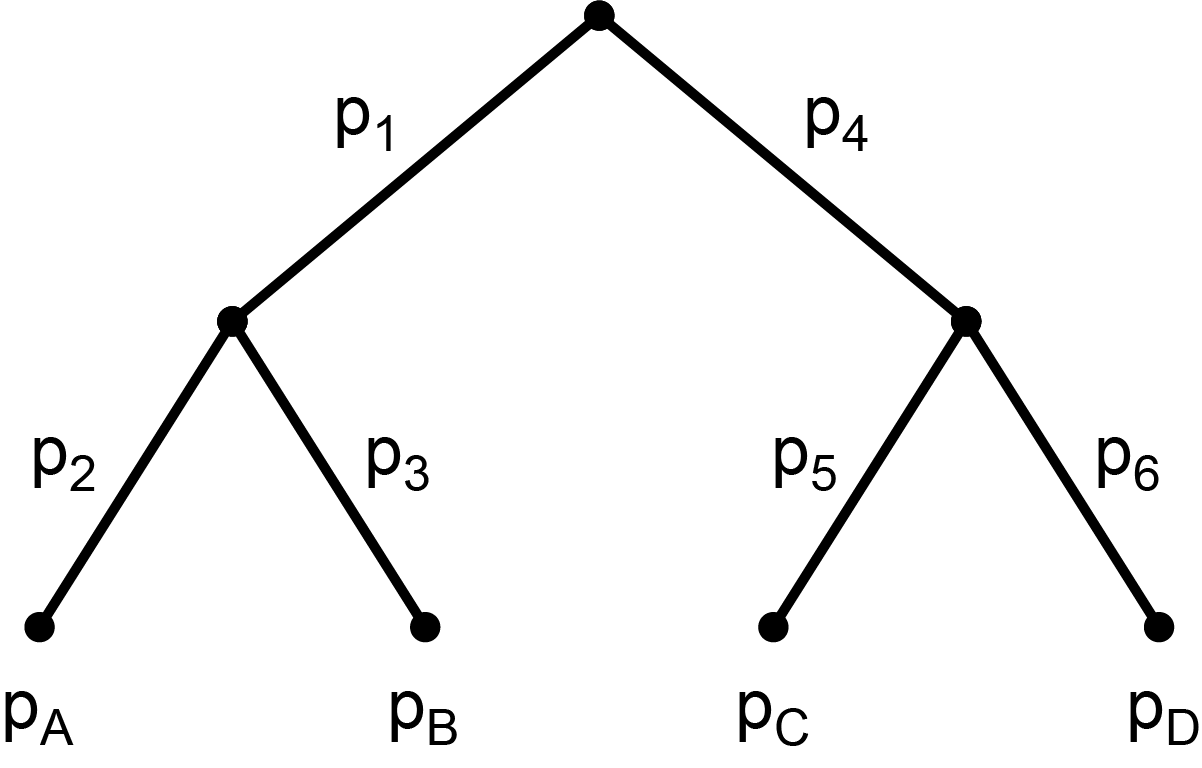
Aus dem nachfolgend abgebildeten Baumdiagramm sind die Werte $p_A=29\,\%$, $p_B=13\,\%$ und $p_C=35\,\%$ bekannt. Berechne mit dieser Information die sechs Einzelwahrscheinlichkeiten des Baumdiagramms.

Ein Anbieter von Online-Diensten verkauft Jahresabos. Eine Analyse des Kundenverhaltens ergab folgende Erkenntnisse:   ▪  58.2 % aller Abonnenten nutzen den Online-Dienst auch noch drei Monate nach dem Kauf. Nachfolgend werden diese Kunden als Langzeitnutzer bezeichnet.  ▪  77.9 % der Langzeitnutzer verlängern ihr Abo nach einem Jahr.  ▪  Insgesamt verlängern 55.2 % aller Kunden ihr Abo nach einem Jahr. 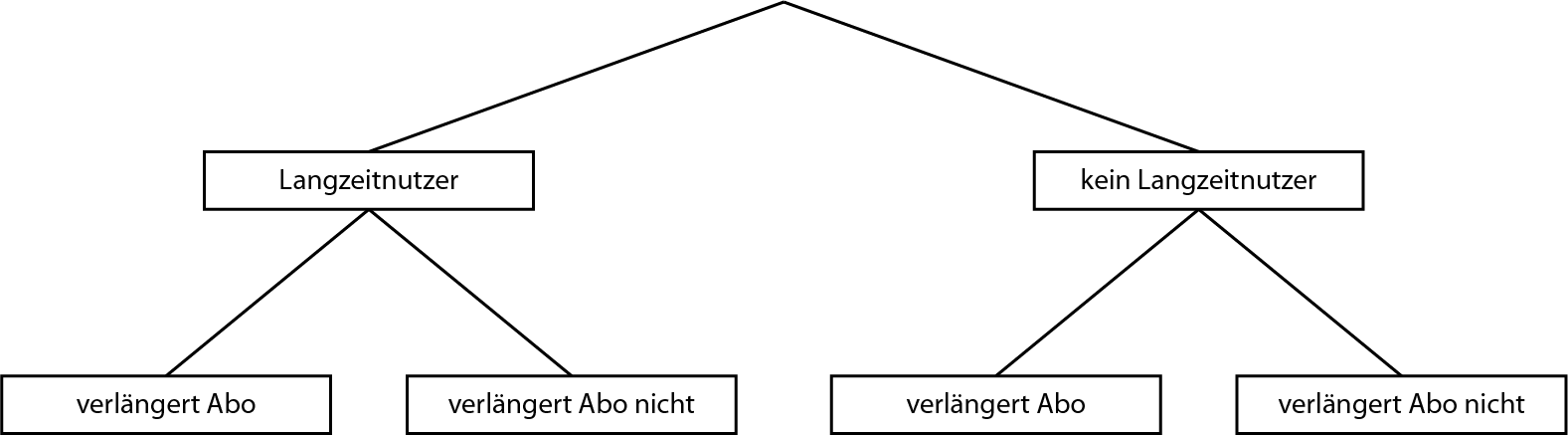Schreibe die entsprechenden Wahrscheinlichkeiten auf die sechs Linien des folgenden Baumdiagramms.

Für diese Aufgabe sind folgende Fachbegriffe relevant:   ▪  Prävalenz: Anteil der Bevölkerung, der an einer bestimmten Krankheit erkrankt ist  ▪  Sensitivität: Wahrscheinlichkeit, mit welcher ein medizinischer Test eine erkrankte Person als krank erkennt  ▪  Spezifität: Wahrscheinlichkeit, mit welcher ein medizinischer Test eine gesunde Person als gesund erkennt Die Sensitivität eines neu entwickelten Tests beträgt 97.6 % während seine Spezifität bei 99.2 % liegt. Laut Schätzungen beträgt die Prävalenz dieser Krankheit 0.55 %. a) Beschrifte das folgende Baumdiagramm vollständig. $K$ bedeutet, dass eine Person erkrankt ist und $\neg K$ ist das zugehörige Gegenereignis. $T+$ steht für ein positivies Testergebnis und $T-$ für ein negatives Testergebnis.

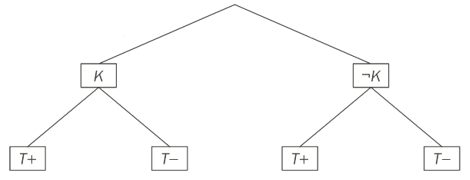
b) Frau Winter erhält ein positives Testergebnis. Wie wahrscheinlich ist es, dass sie tatsächlich an dieser Krankheit erkrankt ist?

Es sind die Wahrscheinlichkeiten $P(A)=32\,\%$ und $P(A\wedge B)=14.4\,\%$ bekannt. Die Ereignisse $A$ und $B$ sind unabhängig. a) Berechne $P(B)$. b) Beschrifte das Baumdiagramm vollständig.

In der ersten Klasse einer HTL erhalten 22.1 % aller Schüler ein „Nicht genügend“ in Mathematik und 7 % der Schüler erhalten in Deutsch ein „Nicht genügend“. 19.4 % der Schüler erhalten in Mathematik ein „Nicht genügend“, sind in Deutsch jedoch positiv. a) Erstelle eine vollständige Vierfeldertafel! b) Wie groß ist die Wahrscheinlichkeit, dass jemand, der in Deutsch kein „Nicht genügend“ hat, in Mathematik ein „Nicht genügend“ bekommt? c) Untersuche anhand dieser Daten, ob sich „Nicht genügend“ in diesen beiden Fächern begünstigen, behindern oder unabhängig sind. Begründe deine Entscheidung anhand konkreter Berechnungen und durch vollständige Sätze.

Es wird der Zusammenhang zwischen dem in der Unterstufe besuchten Schultyp und dem erfolgreichen Abschluss der 1. Klasse einer HTL untersucht. Folgende Daten sind bekannt:   ▪  Insgesamt wurden 140 Schüler untersucht.  ▪  86 Schüler stammen aus einem Gymnasium.  ▪  38 Schüler schafften die 1. Klasse der HTL nicht.  ▪  15 Schüler stammen aus einem Gymnasium und schafften die 1. Klasse der HTL nicht. a) Vervollständige die Vierfeldertafel, indem du die Wahrscheinlichkeiten in die einzelnen Felder schreibst. b) Wie groß ist die Wahrscheinlichkeit, dass ein zufällig ausgewählter Schüler, welcher zuvor die Mittelschule besucht hat, die 1. Klasse der HTL schafft? c) Ein bestimmter Schüler schafft die 1. Klasse der HTL nicht. Mit welcher Wahrscheinlichkeit stammt dieser Schüler aus einer Mittelschule? d) Überprüfe, ob die Ereignisse „kommt aus Gymnasium“ und „schafft 1. Klasse“ stochastisch unabhängig sind. Beschreibe das Ergebnis in einem vollständigen Satz!

Um die Wirksamkeit eines neuen Medikaments zu testen, werden insgesamt 3000 erkrankte Menschen untersucht. 2000 Menschen erhielten das zu testende Medikament. Davon wurden 1621 Menschen gesund. Die anderen 1000 Personen erhielten ein Placebo. Von dieser Gruppe wurden 203 Menschen gesund. a) Erstelle eine vollständig mit relativen Häufigkeiten ausgefüllte und beschriftete Vierfeldertafel. b) Wie groß ist die Wahrscheinlichkeit, dass jemand, der das echte Medikament erhält, gesund wird? c) Herr Karner gehört zu den 3000 Testpersonen. Er wurde gesund. Wie groß ist die Wahrscheinlichkeit, dass er das echte Medikament erhielt?

Es waren zu einem bestimmten Zeitpunkt 0.89 % der Gesamtbevölkerung mit dem Coronavirus infiziert. Bei einem bestimmten Testverfahren erhielten zu diesem Zeitpunkt 1.65 % aller getesteten Personen ein positives Testergebnis. 0,1 % aller getesteten Personen sind infiziert und erhalten ein negatives Testergebnis. a) Berechne die Wahrscheinlichkeit, dass in einer Schulklasse mit 17 Personen mindestens eine Person ein positives Testergebnis erhält, wenn die gesamte Klasse getestet wird. b) Fülle die nachfolgende Vierfeldertafel vollständig aus! c) Eine Person erhält ein positives Testergebnis. Berechne die Wahrscheinlichkeit, dass diese Person tatsächlich mit dem Coronavirus infiziert ist. d) Berechne die sogenannte „Falsch-positiv-Rate“, welche folgendermaßen definiert ist: $P( \mathrm{\,positiver~Test\,} \mid \mathrm{\,nicht~infiziert\,} )$

Bei einem Spiel der vom österreichischen Fernsehsender ORF ausgestrahlten Sendung „Money Maker“ werden auf einem 3×3-Feld zufällig drei Wiener Philharmoniker versteckt. Zwei Spieler decken abwechselnd jeweils ein Feld auf. Jener Spieler, der die dritte Goldmünze aufdeckt, gewinnt. Hat bei diesem Spiel ein Spieler einen Vorteil, also eine Gewinnwahrscheinlichkeit größer als 50 %? Begründe durch eine Rechnung!

Formuliere zu den folgenden Ereignissen jeweils ein passendes Gegenereignis. a) Alle Schüler der Klasse wohnen in Wien. b) Kein Schüler der Klasse ist älter als 17 Jahre. c) Alle Schüler der Klasse haben bei der letzten Schularbeit ein Ergebnis zwischen 8 und 18 Punkten erreicht.

Herr Gruber installiert an seinem Wohnhaus eine Alarmanlage. Laut Hersteller wird bei 96.2 % aller Einbrüche ein Alarm ausgelöst. Die Wahrscheinlichkeit, dass an einem Tag ein falscher Alarm ausgelöst wird (z. B. durch ein Tier oder durch den Wind) beträgt 0.23 %. Allgemein beträgt die tägliche Einbruchswahrscheinlichkeit für ein Wohnhaus in Herrn Grubers Wohngebiet 0.044 %. a) Erstelle ein passendes Baumdiagramm, welches alle Informationen des obigen Textes enthält. b) Wie groß ist die Wahrscheinlichkeit, dass an einem bestimmten Tag ein Alarm ausgelöst wird? c) Herr Gruber sieht auf seinem Smartphone, dass ein Alarm ausgelöst wurde. Mit welcher Wahrscheinlichkeit handelt es sich um einen Einbruch?

Valentin spielt gegen Anna und Benjamin Tischtennis. Es ist vereinbart, dass insgesamt drei Spiele gespielt werden, wobei sich Anna und Benjamin jeweils abwechseln. Valentin gilt als Sieger, wenn er beide Gegner besiegt hat bzw. anders formuliert, wenn er zwei aufeinanderfolgende Spiele gewinnt. Valentin schätzt, dass er Anna mit einer Wahrscheinlichkeit von 60 Prozent und Benjamin mit einer Wahrscheinlichkeit von $\frac{1}{3}$ besiegt. Bei welcher Reihenfolge (ABA oder BAB) hätte er die größeren Siegeschancen? Begründe dein Ergebnis rechnerisch!

Bei einem Kartenspiel mit 32 Karten werden zwei zufällige Karten gezogen. Berechne die Wahrscheinlichkeit, mindestens eine Herzkarte zu ziehen (davon gibt es insgesamt 8 Stück).

Ein bestimmter Fußballtormann hält einen Elfmeter mit einer Wahrscheinlichkeit von 18 %. In einem besonders turbulenten Spiel werden drei Elfmeter auf sein Tor geschossen. Beschreibe in Worten, was durch den Term $1-0{,}82^3$ berechnet wird!

In Geographie werden in Pauls Klasse jede Unterrichtsstunde zufällig zwei verschiedene Schüler zur Stundenwiederholung aufgerufen. Es sind insgesamt 15 Schüler anwesend. Wie groß ist die Wahrscheinlichkeit, dass Paul an diesem Tag aufgerufen wird?

Finde jeweils eine passende Formulierung für das zugehörige Gegenereignis! a) Mehr als 284 Studierende haben die Prüfung bestanden. b) Emma hat mindestens 38 Punkte und weniger als 52 Punkte erreicht. c) Niklas und Lena haben die Prüfung nicht bestanden.

Bei einer Verlosung gibt es dreimal so viele Nieten wie Gewinnlose. Die Wahrscheinlichkeit, dass man mit zwei gekauften Losen genau zwei Gewinne erhält, beträgt 6 %. Berechne die Anzahl der anfangs vorhandenen Lose.

Bei einer Verlosung gibt es um 85 Nieten mehr als Gewinnlose. Die Wahrscheinlichkeit, dass man mit zwei gekauften Losen genau zwei Gewinne erhält, beträgt $\frac{1}{24}$. Berechne die Anzahl der anfangs vorhandenen Lose.

In einer Schüssel sind 24 rote, 22 blaue und 20 gelbe Kugeln. Wie viele Kugeln muss man mindestens gleichzeitig aus der Schüssel nehmen, um mit Sicherheit mindestens eine Kugel jeder Farbe zu ziehen?

a) Wie viele mögliche Ziehungsergebnisse gibt es beim Lotto 5 aus 40? b) Jemand gibt für eine Ziehung 100 verschiedene Lottoscheine ab. Wie groß ist die Wahrscheinlichkeit, dass von einem dieser Scheine alle Zahlen gezogen werden?