Kurse
Eine komplexe Zahl besteht allgemein aus einem reellen Anteil und aus einem imaginären Anteil. Ein Beispiel einer komplexen Zahl wäre $7+2i$. Die Menge der komplexen Zahlen wird mit dem Symbol $\mathbb{C}$ bezeichnet. Jede reelle Zahl ist ein Spezialfall einer komplexen Zahl, bei welcher der imaginäre Anteil entfällt. Auch imaginäre Zahlen sind Spezialfälle von komplexen Zahlen. Hier entfällt der reelle Anteil. Das nachfolgende Mengendiagramm zeigt die Beziehungen zwischen reellen, imaginären und komplexen Zahlen.
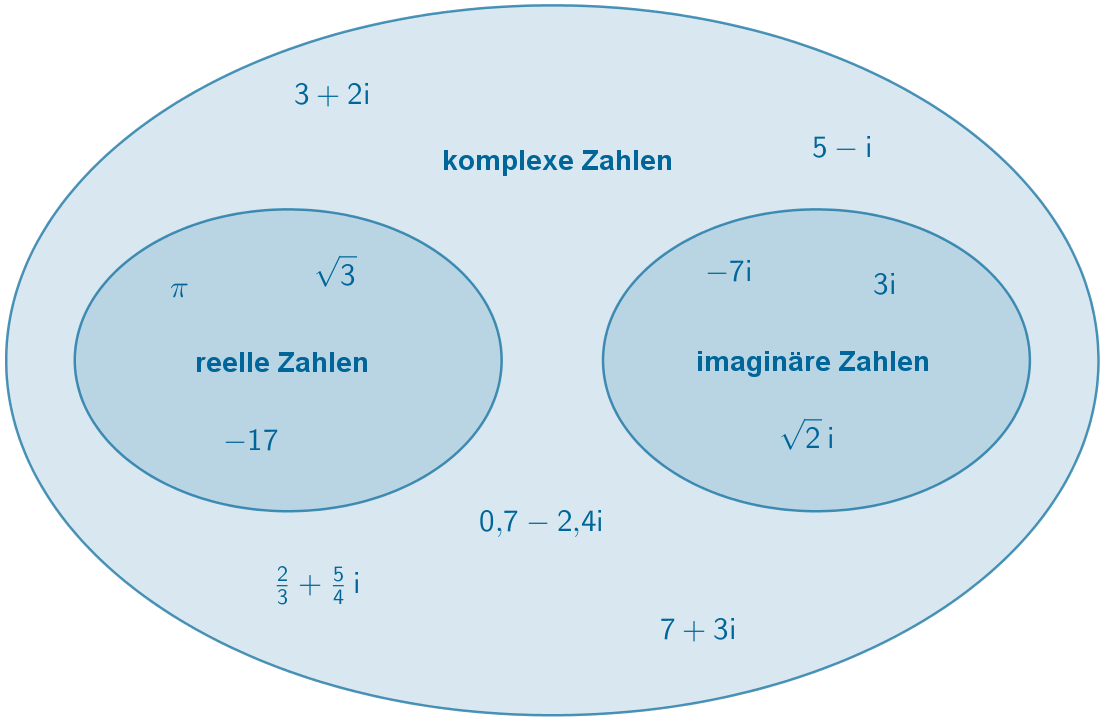

1. Realteil und Imaginärteil
Sei nun $z$ eine beliebige komplexe Zahl. Dann kann man diese Zahl in der Form $z = a + bi$ anschreiben, wobei $a,b \in \mathbb{R}$ gilt. Man verwendet für diese Darstellungsform die Bezeichnungen „kartesische Form“, „algebraische Form“ oder „Komponentenform“. Den reellen Anteil $a$ bezeichnet man als Realteil und schreibt dafür $\mathrm{Re}(z)$. Den Faktor $b$ der imaginären Einheit nennt man Imaginärteil und schreibt dafür $\mathrm{Im}(z)$.
Beispiel 1
Gegeben ist die komplexe Zahl $z = 13 - 7i$. Dann ist $\mathrm{Re}(z) = 13$ und $\mathrm{Im}(z) = -7$.
Aufgabe 1
Löse die folgende Aufgabe: 2@komplexe-zahlen
2. Gaußsche Zahlenebene
Jede reelle Zahl kann man auf der eindimensionalen Zahlengerade einzeichnen. Möchte man auch komplexe Zahlen graphisch darstellen, so muss man die Zahlengerade um eine Dimension erweitern. Man erhält die sogenannte Gaußsche Zahlenebene – ein zweidimensionales Koordinatensystem, bei welchem auf der horizontalen Achse der Realteil und auf der vertikalen Achse der Imaginärteil einer komplexen Zahl aufgetragen wird. Die nachfolgende Abbildung zeigt einige komplexe Zahlen in der Gaußschen Zahlenebene.
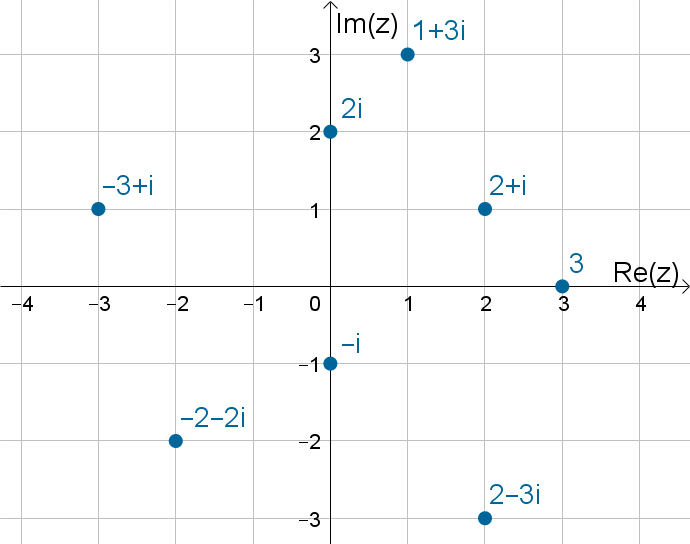
Aufgabe 2
Löse Aufgabe 4 und 5 des folgenden Arbeitsblattes und vergleiche mit den Lösungen auf Seite 3: Arbeitsblatt: Komplexe Zahlen
3. Betrag
Der Betrag einer reellen Zahl gibt an, wie weit diese vom Ursprung der Zahlengerade entfernt ist. Analog dazu beschreibt der Betrag einer komplexen Zahl, wie weit diese vom Ursprung der Gaußschen Zahlenebene entfernt ist. Man kann den Betrag durch den Satz von Pythagoras berechnen. Für $z = a + b\cdot i$ gilt $|z| = \sqrt{a^2 + b^2}$.
Beispiel 2
Es soll der Betrag der komplexen Zahl $z = 12 - 5i$ berechnet werden.
$$|z|=\sqrt{12^2 + (-5)^2} = \sqrt{169}=13$$
Aufgabe 3
Löse die folgenden Aufgaben: 1@komplexe-zahlen, 3@komplexe-zahlen
Aufgabe 4
Löse Aufgabe 2 des folgenden Arbeitsblattes und vergleiche mit den Lösungen auf Seite 3: Arbeitsblatt: Komplexe Zahlen
4. Komplex konjugierte Zahl
Gegeben ist eine komplex Zahl $z = a + b\cdot i$. Die zu $z$ komplex konjugierte Zahl wird meistens mit $\bar z$ oder mit $z^*$ bezeichnet. Man erhält sie aus der gegebenen Zahl $z$, indem man das Vorzeichen des Imaginärteils ändert. Benötigt wird sie u. a. für die Division von komplexen Zahlen.
Beispiel 3
Gegeben sind die komplexen Zahlen $z_1 = 3 + 2i$, $z_2 = -5 -3i$ und $z_3 = 4i$.
Die zugehörigen komplex konjugierten Zahlen lauten $\bar{z}_1 = 3 - 2i$, $\bar{z}_2 = -5 + 3i$ und $\bar{z}_3 = -4i$.
Aufgabe 5
Löse die folgende Aufgabe: 8@komplexe-zahlen
Aufgabe 6
Löse Aufgabe 3 des folgenden Arbeitsblattes und vergleiche mit den Lösungen auf Seite 3: Arbeitsblatt: Komplexe Zahlen
Aufgabe 7
Überprüfe, was passiert, wenn man eine komplexe Zahl mit der zugehörigen komplex konjugierten Zahl multipliziert.
In der Gaußschen Zahlenebene entspricht die komplexe Konjugation einer Spiegelung der Zahl an der reellen Achse.
© 2016 – 2024 MATHE.ZONE