Grundlagen | Textaufgaben zu Exponentialfunktionen

Häufig soll die Funktionsgleichung einer Exponentialfunktion erst bestimmt werden, um damit weitere Berechnungen durchzuführen. Je nachdem, welche Informationen bekannt sind, kann die Funktionsgleichung auf verschiedene Arten bestimmt werden. Falls zwei Punkte des Funktionsgraphen bekannt sind, werden die Koordinaten der Wertepaare in die allgemeine Funktionsgleichung $f(x) = c \cdot a^x$ eingesetzt. Durch Lösen des entstehenden Gleichungssystems werden die Parameter $a$ und $c$ berechnet. Es handelt sich dabei um kein lineares Gleichungssystem.

Nach 7 Stunden betrug die Konzentration eines Medikaments im Blut 12 μg/L. Nach 10 Stunden waren es nur noch 5 μg/L. Es soll die zugehörige exponentielle Abnahmefunktion bestimmt werden. Durch Einsetzen der Wertepaare erhält man das folgende Gleichungssystem: $$12=c\cdot a^7$$ $$5=c\cdot a^{10}$$ Formt man die erste Gleichung nach $c$ um, so erhält man $c = \frac{12}{a^7}$. Durch Einsetzen in die zweite Gleichung kann $a$ berechnet werden: $$5=\frac{12}{a^7}\cdot a^{10}=12a^3$$ $$a=\sqrt[3]{\frac{5}{12}} \approx 0{,}7469 $$ Für $c$ erhält man Folgendes: $$c=\frac{12}{a^7} \approx \frac{12}{0{,}7469^7} \approx 92{,}54$$ Die gesuchte Funktionsgleichung lautet daher $f(t) \approx 92{,}54\cdot 0{,}7469^t$.

Im folgenden Video wird dieser Aufgabentyp anhand von zwei Beispielen erklärt:

Löse die folgende Aufgabe: 17@exponentialfunktionen

Häufig ist der Funktionsgraph einer Exponentialfunktion bekannt und es soll damit eine passende Funktionsgleichung bestimmt werden. Man liest dazu zwei Punkte des Funktionsgraphen ab und erstellt anhand dieser Punkte die Funktionsgleichung (wie oben beschrieben). Falls es Punkte gibt, die man exakt ablesen kann, so sollten diese Punkte auf jeden Fall verwendet werden. Ansonsten sollten zwei gut ablesbare Punkte gesucht werden, die möglichst weit voneinander entfernt sind (damit sich Ungenauigkeiten beim Ablesen nicht so stark auf das Ergebnis auswirken).

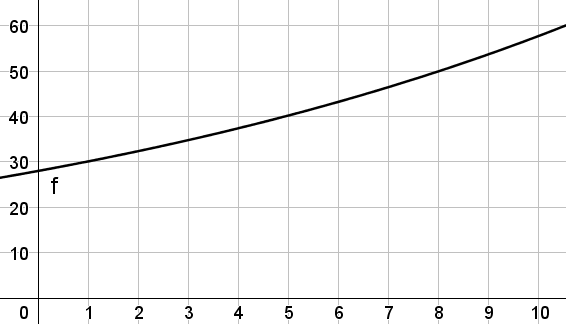
Es soll die Funktionsgleichung einer Exponentialfunktion bestimmt werden, welche zum nachfolgenden Funktionsgraph passt. Man wählt dazu zwei möglichst exakt ablesbare Punkte deren Abstand so groß wie möglich ist. Gut geeignet sind die Punkte $(1\mid 30)$ und $(8\mid 50)$. Anhand dieser Punkte ermittelt man die Funktionsgleichung (wie im vorherigen Kapitel beschrieben). Das Ergebnis lautet $f(x)\approx 27{,}89 \cdot 1{,}0757^x$.

Löse die folgenden Aufgaben: #552, #122

Kapitelübersicht · Kursübersicht