Kurse
keine vorherige Lektion vorhanden |
Funktionsgleichung erstellen
Eine Funktion, deren Funktionsgleichung die Form $f(x) = c\cdot a^x$ hat, nennt man Exponentialfunktion.
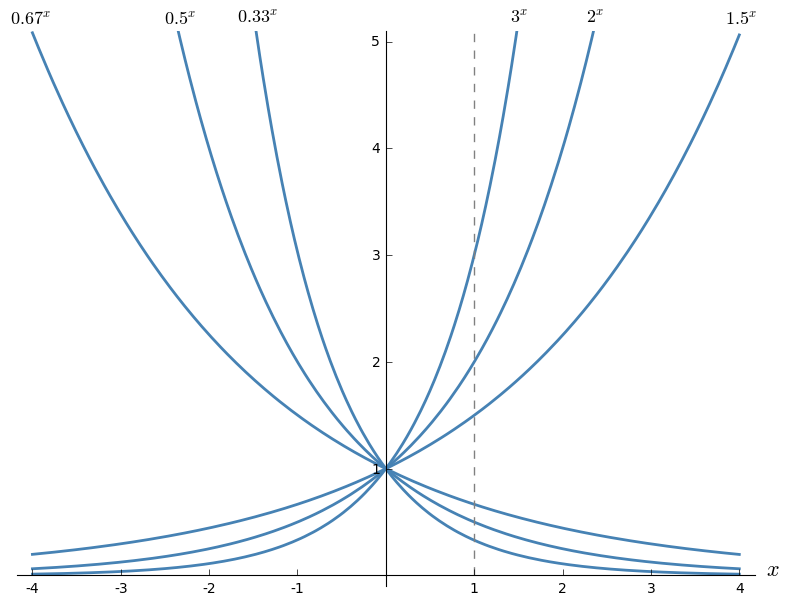
1. Einsatzbeispiele
Nachfolgend werden einige typische Beispiele für exponentielle Wachstums- bzw. Abnahmeprozesse aufgelistet:
- Ausbreitung von Krankheiten
- Radioaktiver Zerfall
- Entwicklung der Einwohnerzahl
- Wachstum von Bakterienpopulationen
- Zinseszinsen
- Abnahme der Intensität von Licht (und anderen Arten von Strahlung) in Materie
- Abbau von Medikamenten bzw. chemischen Substanzen im Körper
2. Bedeutung der Parameter a und c
Der Parameter $c$ entspricht dem Ordinatenabschnitt. Er gibt also an, in welcher Höhe die $y$-Achse geschnitten wird. Begründen kann man dies, indem man $x=0$ in den Funktionsterm einsetzt. Man erhält $c\cdot a^0 = c \cdot 1 = c$.
Der Parameter $a$ wird häufig Änderungsfaktor genannt. Es muss sich um eine positive reelle Zahl ungleich 1 handeln. Je nachdem, welchen Wert $a$ hat, unterscheidet man zwei wesentliche Klassen von Exponentialfunktionen:
- Für $a>1$ ist die Exponentialfunktion ansteigend (je größer $a$ ist, umso schneller wächst die Funktion im positiven Bereich).
- Falls $0 < a<1$ erfüllt ist (also $a$ zwischen 0 und 1 liegt), so ist die Exponentialfunktion fallend (je kleiner $a$ ist, umso schneller sinkt die Funktion im positiven Bereich).

Beispiel 1
Es soll die Funktionsgleichung der folgenden Funktionsgraphen bestimmt werden:
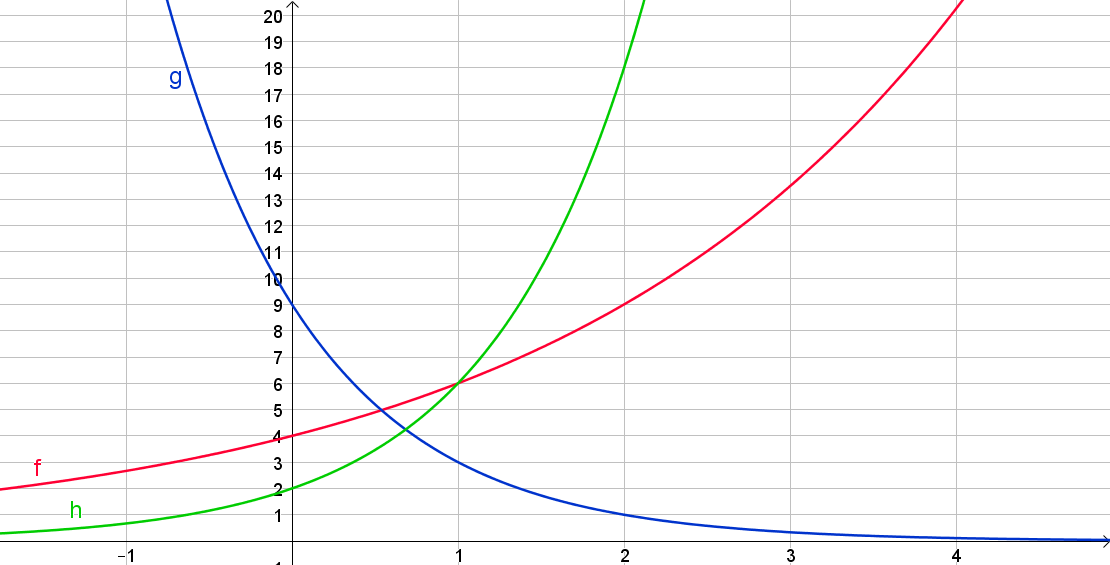
Die Funktion $f$ schneidet die $y$-Achse beim Wert 4. Somit ist $c=4$. An der Stelle 1 besitzt sie den Wert 6 und an der Stelle 2 besitzt sie den Wert 9. Es wird also jeweils mit dem Faktor 1,5 multipliziert, wenn $x$ um 1 größer wird. Daher ist der Änderungsfaktor 1,5 und man erhält die Funktionsgleichung $f(x)=4\cdot 1{,}5^x$.
Die Funktion $g$ besitzt den Ordinatenabschnitt 9. An der Stelle 1 beträgt der Wert nur noch 3. Es wurde also mit dem Faktor $\frac{1}{3}$ multipliziert. Daraus folgt die Funktionsgleichung $g(x)=9\cdot \left( \frac{1}{3}\right) ^x$. Die Klammer um den Bruch $\frac{1}{3}$ ist wichtig, denn würde man $\frac{1}{3}^x$ schreiben, so würde nur der Zähler 1 potenziert werden.
Die Funktion $h$ besitzt den Ordinatenabschnitt 2. An der Stelle 1 beträgt der Funktionswert 6, was zu einem Änderungsfaktor von 3 führt. Die Funktionsgleichung lautet daher $h(x)=2\cdot 3^x$.

Aufgabe 1
Ermittle die Funktionsgleichungen der folgenden Funktionsgraphen.

Lösungen:
ausklappen

Aufgabe 2
Zeichne die Funktionsgraphen von $f(x)=5\cdot 4^x$ und $g(x)=30\cdot \left( \frac{2}{3} \right)^x$ jeweils in ein eigenes Koordinatensystem. Wähle zuvor eine passende Achsenskalierung.
Aufgabe 3
Löse die folgende Aufgabe: #563
3. Allgemeine Eigenschaften
Wie man anhand der obigen Graphen erkennen kann, erfüllen Exponentialfunktionen folgende Eigenschaften:
- Exponentialfunktionen haben keine Nullstelle und sind überall positiv.
- Für $a>1$ sind Exponentialfunktionen streng monoton steigend.
- Für $ 0 < a < 1 $ sind Exponentialfunktionen streng monoton fallend.
- Sind die Basen Kehrwerte, dann sind die Funktionsgraphen bezüglich der vertikalen Achse gespiegelt.
© 2016 – 2024 MATHE.ZONE