Aufgaben zu linearen Gleichungssystemen
Dieser Bereich der Website befindet sich im Umbau.
Betrachten Sie daher auch folgende Arbeitsblätter für mehr Aufgaben zu diesem Thema:
1. Allgemeine Textaufgaben (zwei Variablen)
#270 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
In einem Unternehmen arbeiten dreimal so viele Männer wie Frauen bzw. anders ausgedrückt um 32 Männer mehr als Frauen.
a) Kreuze alle zutreffenden Aussagen an, wenn x die Anzahl der Männer und y die Anzahl der Frauen beschreibt.
x−y=32
y−x=32
x=3y
y=3x
b) Berechne, wie viele Männer und wie viele Frauen in diesem Unternehmen arbeiten.
2. Lösungsfälle (zwei Variablen)
Ergänze die Lücken des folgenden linearen Gleichungssystems so, dass dieses unendlich viele Lösungen besitzt.
[1] 2a+7b=50
[2] 20a+_b=_
3. Grafisches Lösungsverfahren (zwei Variablen)
#1240 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Löse das folgende lineare Gleichungssystem grafisch!
[1] 5x+2y=3
[2] 4x−5y=6
4. Bewegungsaufgaben (zwei Variablen)
Ein Motorboot fährt bei gleicher Motorleistung flussaufwärts mit einer Geschwindigkeit von 29.4 km/h und flussabwärts mit 44.1 km/h. Wie groß sind die Eigengeschwindigkeit des Bootes und die Fließgeschwindigkeit des Flusses?
Ein Autofahrer und ein Motorradfahrer wohnen 368 km voneinander entfernt und fahren einander entgegen. Wenn beide um 8:00 Uhr wegfahren, treffen sie einander um 10:31 Uhr. Fährt der Motorradfahrer um 8:00 Uhr weg, aber der Autofahrer erst um 9:30 Uhr, so begegnen sie einander um 11:17 Uhr. Berechne die mittleren Geschwindigkeiten beider Fahrzeuge!
5. Lineare Gleichungssysteme mit mehr als zwei Variablen
Bei der sogenannten Dreieck-Stern-Transformation wird eine dreieckförmige Anordnung von Widerständen in eine gleichwertige sternförmige Anordnung umgewandelt.
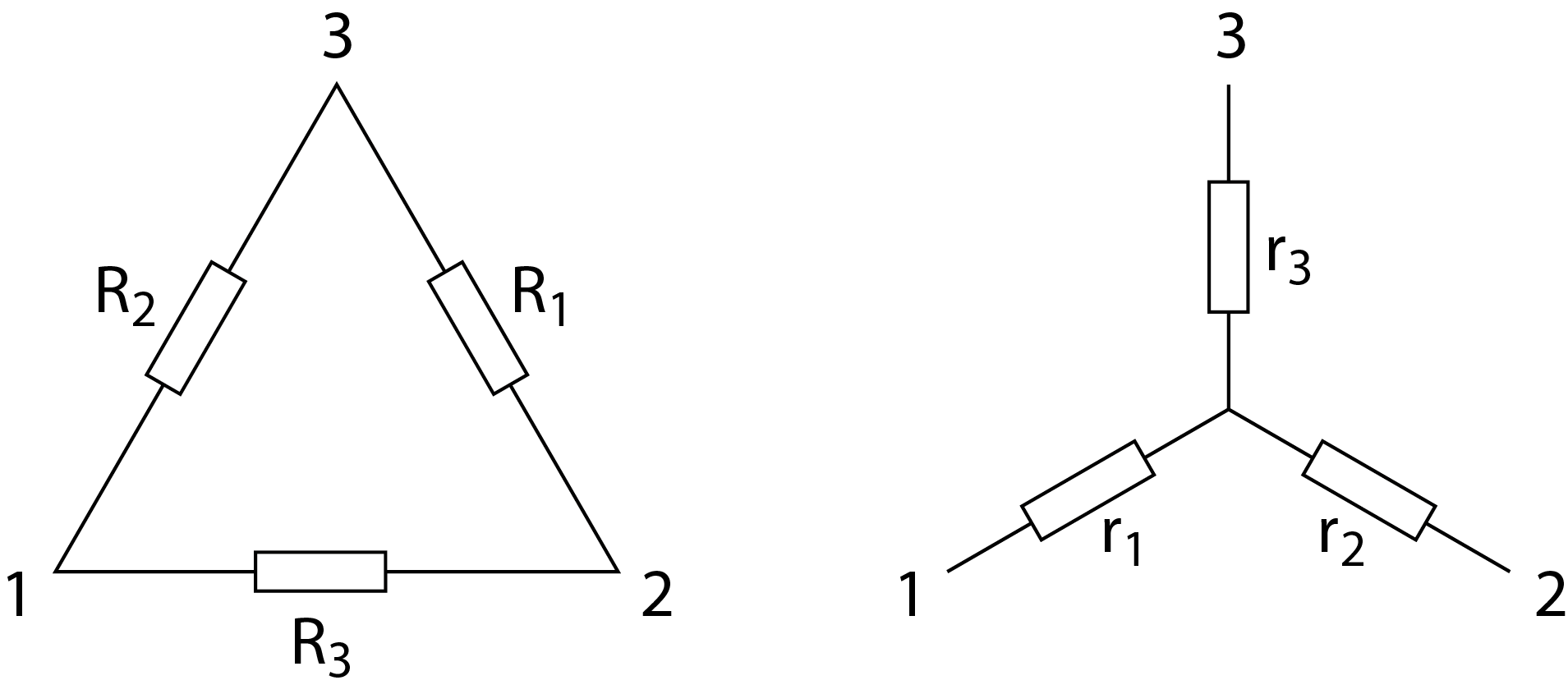

Dafür gelten die folgenden Zusammenhänge:
r1+r2=R3⋅(R1+R2)R1+R2+R3r2+r3=R1⋅(R2+R3)R1+R2+R3r1+r3=R2⋅(R1+R3)R1+R2+R3
Berechne die Widerstände r1,r2,r3 der sternförmigen Schaltung, wenn die Widerstände der Dreiecksschaltung folgende sind: R1=21Ω, R2=37Ω, R3=56Ω.
Gegeben ist die unten abgebildete elektrische Schaltung, wobei U=29.1V, R1=2.5Ω, R2=3.8Ω und R3=7Ω bekannt sind.
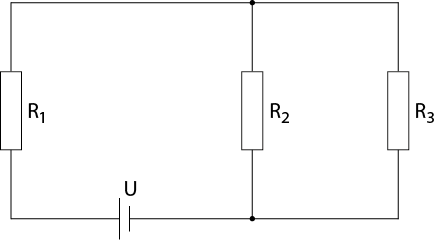
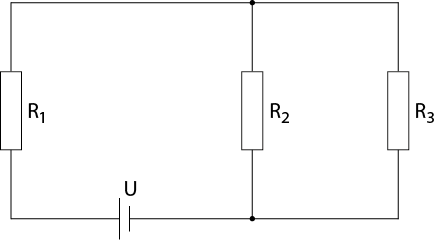
Anhand der Kirchhoffschen Regeln (Knotenregel und Maschenregel) sowie des Ohmschen Gesetzes können folgende Zusammenhänge festgestellt werden:
I1=I2+I3I1R1+I3R3=UI2R2=I3R3
Bereche die Ströme I1,I2 und I3, welche durch die jeweiligen Widerstände fließen.
#1147 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Addiert man jeweils zwei Winkel eines ebenen Dreiecks, so erhält man 129.1° und 136.8°. Berechne die drei Winkel des Dreiecks.
6. Lineare Gleichungssysteme mittels Matrizen lösen
#1277 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Es ist das folgende lineare Gleichungssystem gegeben:
[1] 2x+3y=4
[2] 6x+9y=−13
a) Berechne die Determinante der zugehörigen Koeffizientenmatrix.
b) Erkläre, wie man anhand dieser Determinante erkennen kann, dass dieses Gleichungssystem keine eindeutige Lösung besitzt.
© 2016 – 2025 MATHE.ZONE