Wandle die folgenden Winkelangaben jeweils in Grad, Winkelminuten und Winkelsekunden um. Runde die Winkelsekunden gegebenenfalls auf eine ganze Zahl. a) $48.2969^\circ$ b) $648.64'$ c) $29571''$

Wandle die folgenden Winkelangaben jeweils in Grad um. a) $19^\circ~52'~22''$ b) $32'~21''$

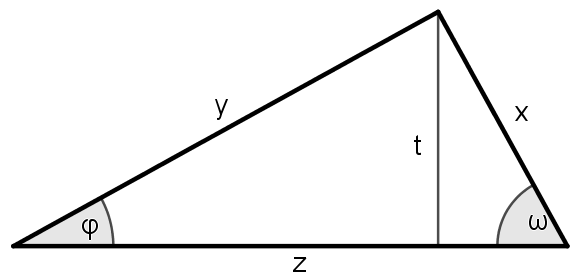
Vom nachfolgend abgebildeten rechtwinkligen Dreieck sind die Kathete $x=7$ cm und die Hypotenuse $z=16.3$ cm bekannt. Berechne die fehlende Kathete $y$, den Flächeninhalt $A$ und die Höhe $t$. Die Skizze ist nicht maßstabsgetreu.

Sabrina möchte bestimmen, wie hoch der Baum in ihrem Garten ist. Sie misst dazu die Länge ihres eigenen Schattens (1.6 m) sowie die Länge des Baumschattens (18.2 m). Ihre Körpergröße beträgt 171 cm. Wie hoch ist der Baum ungefähr?

Ein ursprünglich 39 m hoher Baum ist aufgrund eines Sturms so abgeknickt, dass seine Spitze 17 m vom Stamm entfernt den Boden berührt. In welcher Höhe ist der Baum abgeknickt?

Bei einem Sturm wurde ein Baum in einer Höhe von 8 m abgeknickt. Die Spitze des Baumes berührt den Boden in 6 m Entfernung vom Baumstamm. Wie hoch war der Baum?

Ein Dreieck hat die Winkel $\alpha=33.52\,^\circ$ und $\beta=106.2\,^\circ$. Berechne den fehlenden Winkel $\gamma$.

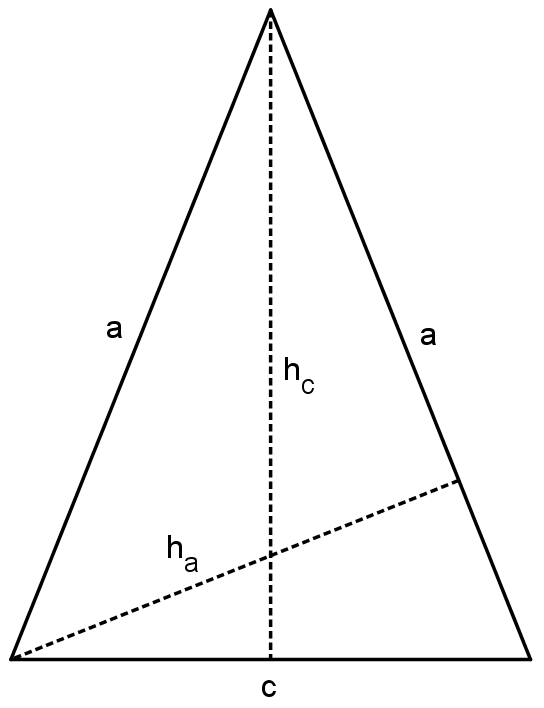
Von einem gleichschenkligen Dreieck kennt man den Flächeninhalt $A=31.13$ cm² und die Höhe $h_c=42$ mm. Berechne die Seitenlängen $a$ und $c$ sowie die Höhe $h_a$. Achte dabei auf die Einheiten. Die Benennung der Variablen ist der abgebildeten nicht maßstabsgetreuen Skizze zu entnehmen.

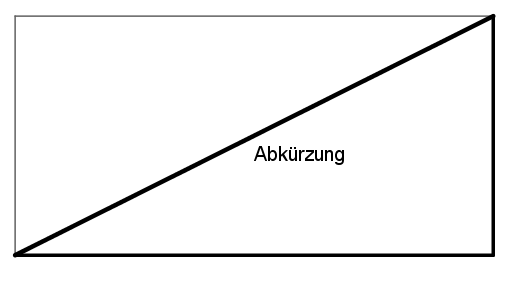
Der Schulweg von Thomas führt an einer 239 m × 98 m großen, rechteckigen Wiese vorbei. Thomas entscheidet sich dazu, die Wiese diagonal zu durchqueren, anstatt wie sonst immer, am Gehweg zu gehen. Welche Distanz erspart er sich durch diese Abkürzung?

Gib an, ob die folgenden Aussagen wahr oder falsch sind. wahr falsch Jedes Dreieck ist durch die Angabe von zwei unabhängigen Größen vollständig bestimmt. wahr falsch Ein rechtwinkliges Dreieck ist durch die Angabe von zwei unabhängigen Größen vollständig bestimmt. wahr falsch Ein gleichseitiges Dreieck ist durch die Angabe einer einzigen Größe vollständig bestimmt.

Eine Person mit Aughöhe 1.7 m steht am Dach eines 22 m hohen Turms. 45 m vor dem Turm befindet sich eine 3.5 m hohe Mauer. Die Person sieht über die Mauer hinweg gerade noch das näher gelegene Ufer eines Flusses. a) Erstelle eine vollständig beschriftete Skizze des Sachverhalts. b) Berechne, wie weit der Fluss horizontal gemessen vom Turm entfernt ist.

Eine 4.2 m lange Leiter muss am Boden einen Mindestabstand von 1.4 m zur Mauer haben, damit sie nicht umkippt. Was ist die maximal zulässige Höhe, in welcher die Leiter an die Mauer angelehnt werden darf?

Ermittle die drei Seitenlängen eines beliebigen rechtwinkligen Dreiecks, dessen Umfang 100 cm beträgt. Die Seitenlängen müssen nicht ganzzahlig sein. Dokumentiere deine Vorgehensweise!

Gegeben ist ein Dreieck mit den Seitenlängen $x = 7$ cm und $y = 34$ cm. Wähle die fehlende Seitenlänge $z$ jeweils so, dass die folgenden Eigenschaften erfüllt sind. a) Das Dreieck ist nicht konstruierbar. b) Das Dreieck ist gleichschenklig. c) Das Dreieck ist rechtwinklig.

Gib an, ob die folgenden Aussagen wahr oder falsch sind. wahr falsch Die drei Innenwinkel eines gleichseitigen Dreiecks betragen jeweils 120°. wahr falsch Ein Dreieck mit zwei gleichen Winkeln ist immer gleichschenklig. wahr falsch Bei einem gleichseitigen Dreieck sind alle drei Winkel gleich groß. wahr falsch Haben zwei Winkel eines Dreiecks 60°, dann handelt es sich immer um ein gleichseitiges Dreieck. wahr falsch Jedes rechtwinklige Dreieck hat zwei spitze Winkel. wahr falsch Jedes Dreieck mit zwei spitzen Winkeln ist rechtwinklig. wahr falsch Ein Dreieck mit den Winkeln 30° und 60° ist immer rechtwinklig.

Gib an, ob die folgenden Aussagen wahr oder falsch sind. wahr falsch Ein Dreieck mit den Seitenlängen 6 cm, 8 cm und 10 cm ist rechtwinklig. wahr falsch Ein Dreieck mit den Seitenlängen 5 cm, 10 cm und 15 cm ist rechtwinklig. wahr falsch Ein Dreieck mit den Seitenlängen 8 cm, 15 cm und 17 cm ist rechtwinklig. wahr falsch Es gibt kein Dreieck mit den Seitenlängen 17 cm, 23 cm und 49 cm. wahr falsch Es gibt kein Dreieck mit den Seitenlängen 52 cm, 49 cm und 98 cm.

Der Flächeninhalt eines gleichseitigen Dreiecks beträgt 4.6 cm². Berechne die Seitenlänge $a$, die Höhe $h$ und den Winkel $\alpha$.

Aus der folgenden Abbildung sind die Seitenlängen $a_1=46\,\mathrm{m}$, $b_1=39\,\mathrm{m}$ und $b_2=64\,\mathrm{m}$ bekannt.

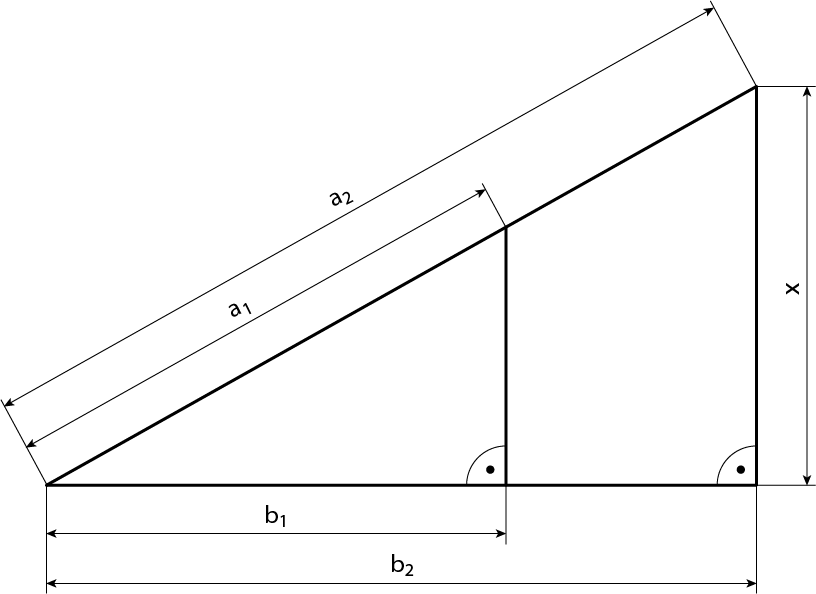
a) Berechne die Seitenlänge $a_2$. b) Berechne die Seitenlänge $x$.

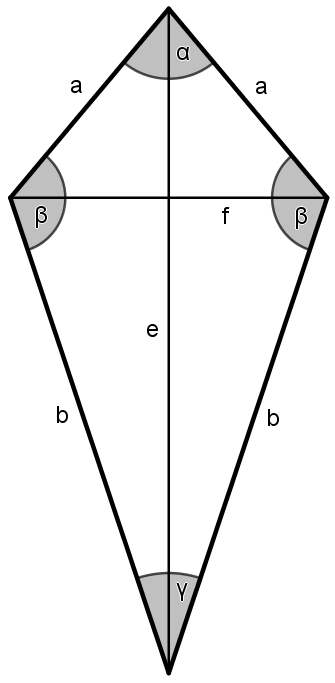
Von einem Deltoid sind die beiden Diagonalen sowie eine Seitenlänge bekannt. Die Werte sind $e=13$ cm, $f=6.1$ cm und $a=7.2$ cm. Die Benennung der Größen ist der unten abgebildeten nicht maßstabsgetreuen Skizze zu entnehmen. Berechne die Seitenlänge $b$ und den Flächeninhalt $A$.

Nachfolgende Abbildung zeigt den Grundriss eines Zimmers.

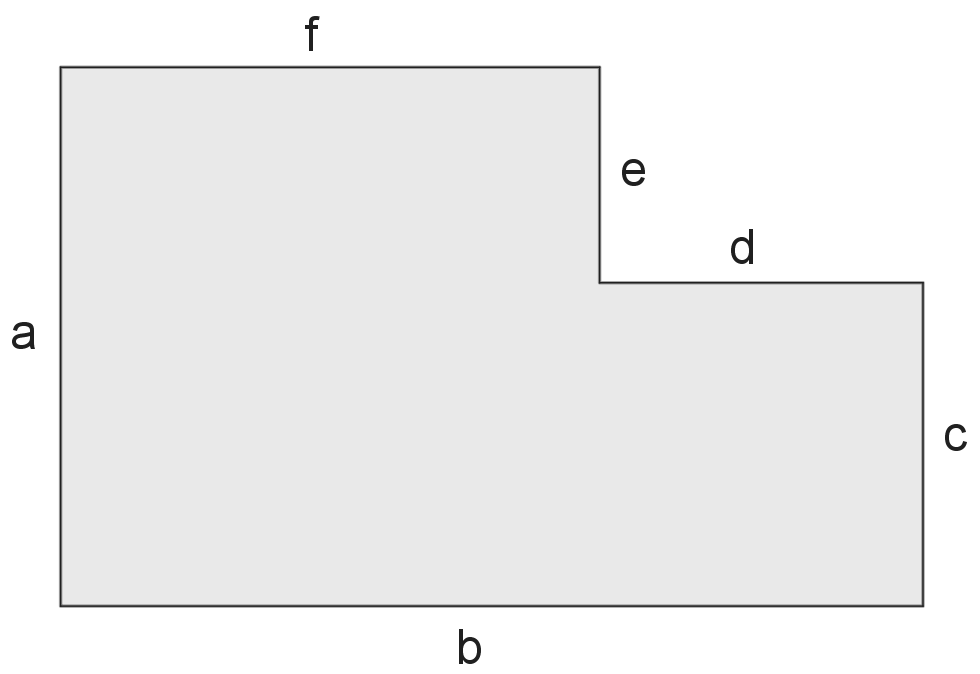
Kreuze jeweils an, ob die nachfolgenden Terme geeignet sind, um die Wohnfläche zu berechnen. geeignet nicht geeignet $a\cdot f+c\cdot d$ geeignet nicht geeignet $a\cdot f+b\cdot c$ geeignet nicht geeignet $e\cdot f+c\cdot d$ geeignet nicht geeignet $b\cdot c+e\cdot f$ geeignet nicht geeignet $a\cdot b-d\cdot e$

Ein 166×129 mm großes Stück Stahlblech wird an den Ecken abgerundet (siehe Skizze). Der Radius dieser Rundungen beträgt 20 mm.

a) Berechne den Umfang. b) Berechne den Flächeninhalt.

Bei einer Leichtathletikanlage haben die Geraden eine Länge von 84,39 m. Der Radius der Innenbahn beträgt 36,5 m. Die gesamte Laufbahn ist 9,76 m breit. Somit ist der Außenradius der Laufbahn 46,26 m. Alle Abmessungen sind unten in einer nicht maßstabgetreuen Skizze abgebildet.

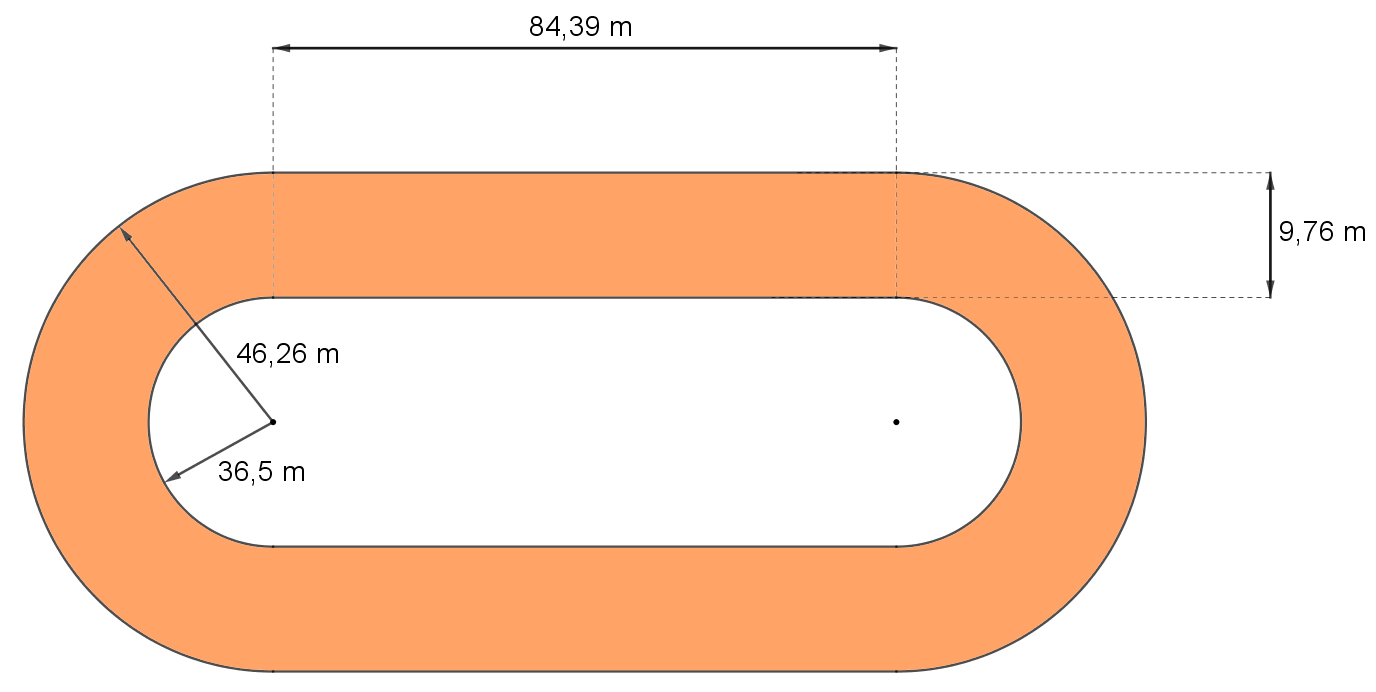
a) Berechne die Länge der Innenbahn. b) Berechne den Flächeninhalt der gesamten Laufbahn.

Es ist die Skizze einer geometrischen Figur abgebildet.

Für die folgenden beiden Aufgaben dürfen nur die Variablen $a,b,c,d$ verwendet werden. a) Erstelle eine möglichst einfache Formel zur Berechnung des Umfangs der Figur. b) Erstelle eine möglichst einfache Formel zur Berechnung des Flächeninhalts der Figur.

Aus einem Rechteck mit den Seitenlängen 212 cm und 122 cm wird ein Halbkreis mit Durchmesser 118 cm ausgeschnitten (siehe Skizze). Berechne den Umfang und den Flächeninhalt der entstehenden Figur.

Nachfolgend ist die Skizze eines Bauteils dargestellt, welches aus 2.5 mm dickem Stahlblech hergestellt werden soll (alle Angaben in Millimeter). Achte auf die Einheiten!

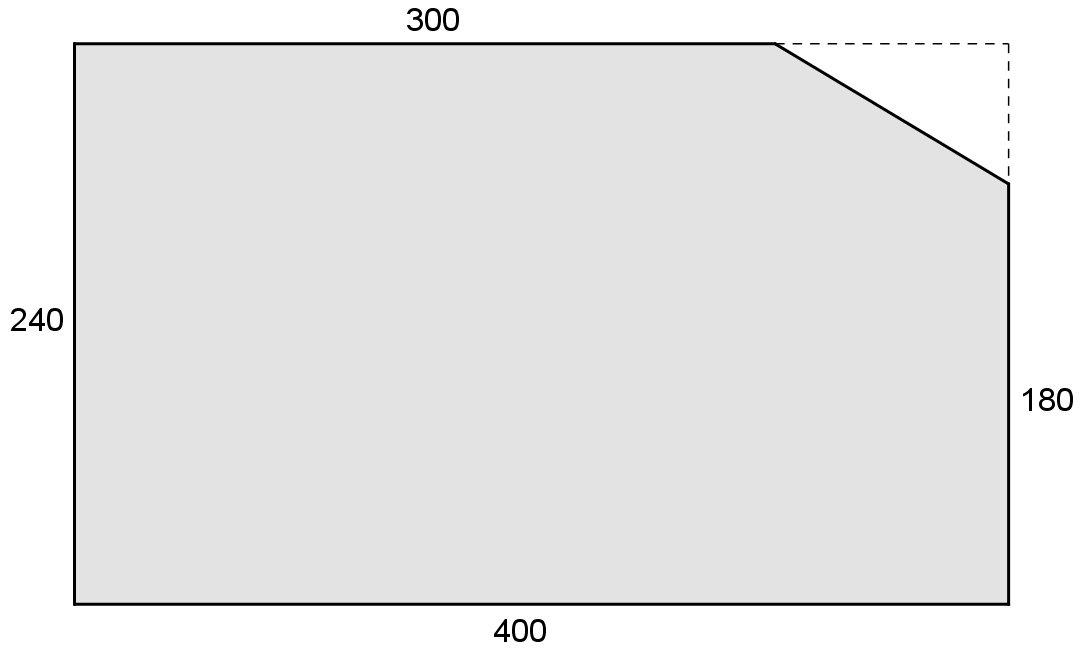
a) Berechne den Flächeninhalt dieses Bauteils. b) Berechne die Masse des Bauteils. Die Dichte von Stahl beträgt 7,85 g/cm³.

Das Dach einer 28.2 m langen und 22.9 m breiten Halle soll neu gedeckt werden. Es handelt sich dabei um ein sogenanntes Pultdach, das entlang der kürzeren Wand der Halle um 2.4 m abfallend ist und nicht über die Wände hinausragt. Bestimme den Flächeninhalt des Daches.

Ein Aufzug eines Krankenhauses ist 2.8 m breit und 4.5 m lang. Überprüfe rechnerisch, ob ein Krankenhausbett mit einer Breite von 1.4 m und einer Länge von 2.7 m darin um 180° gedreht werden kann. Beschreibe das Ergebnis durch einen vollständigen Satz.

Ein Raum ist 2.59 m hoch. Wie hoch darf ein 77 cm tiefer Kasten höchstens sein, damit man ihn durch frontales Kippen aufstellen kann, ohne an der Decke zu streifen? Erstelle auch eine aussagekräftige und vollständig beschriftete Skizze des Sachverhalts.

Ein ringförmiger Kerzenhalter (siehe Skizze, Bildquelle unbekannt) mit einem Durchmesser von 115 cm soll mit vier gleich langen Ketten an der Decke montiert werden, sodass er sich 2 m unter dieser befindet.

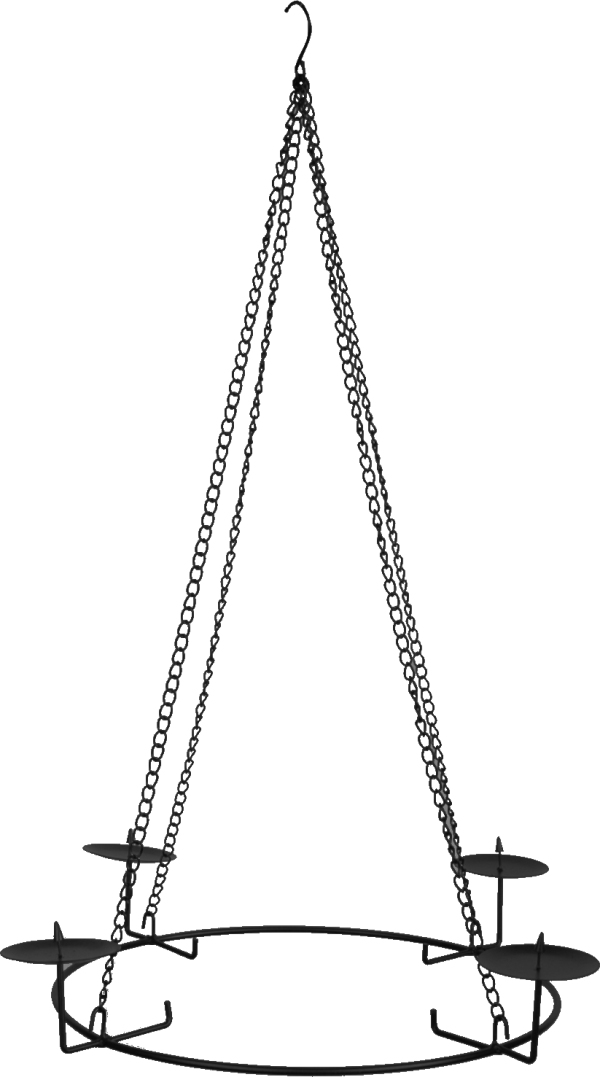
a) Wie lang ist jede einzelne der vier Ketten? b) Wie viel Material muss insgesamt gekauft werden, wenn zur Sicherheit um ein Viertel mehr gekauft wird.

Eine Person ist 1.68 m groß. Ihre Augen befinden sich in einer Höhe von 1.53 m. Es soll ein Spiegel gekauft werden, in dem sich die Person gerade noch vollständig sehen kann. Gib an, in welcher Höhe sich die Ober- und Unterkante befinden müssen.