Aufgaben zu funktionalen Zusammenhängen |
Auf dieser Seite findet man Aufgaben zu funktionalen Zusammenhängen. Jede Aufgabe besitzt eine Nummer, über welche sie durch die Suchfunktion jederzeit wieder aufgerufen werden kann. Dazu muss als Suchbegriff die Aufgabennummer mit einer Raute davor eingegeben werden, also z. B. #123.
Die Aufgaben werden bei jedem Laden der Seite neu generiert. Bei den meisten Aufgaben bedeutet dies, dass sich Werte in der Angabe verändern. Möchte man zu einem späteren Zeitpunkt erneut auf die selbe Aufgabe zugreifen, so sollte ein Screenshot angefertigt werden.
Hinter den Eingabefeldern wird jeweils die Anzahl an Nachkommastellen angegeben. Zur Kontrolle der eigenen Rechnungen können bei vielen Aufgaben die Lösungen eingeblendet werden. Sollte Ihnen bei einer Aufgabe ein Fehler auffallen, so melden Sie diesen bitte.
1. Funktionsbegriff
#618 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Fehler melden
Zeichne den Graph der Funktion $f:\{1,2,3,...,20\}\to \mathbb{N}$, welche jeder natürlichen Zahl $n$ die Anzahl ihrer positiven Teiler zuordnet.
Funktionsgraph: #655 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Fehler melden
Nachfolgend ist die Temperatur im Verlauf eines Tages abgebildet, d. h. jeder Uhrzeit $t$ (in
Stunden) aus dem Intervall $[0,24]$ wird eine Temperatur $T(t)$ (in Grad Celsius) zugeordnet.
a) Gib den Temperaturbereich (die Wertemenge) dieser Funktion als Intervall an.
Temperaturbereich: [1]
b) Was war die niedrigste Temperatur an diesem Tag?
Ergebnis: [1] °C
c) Wie lange betrug die Temperatur mindestens 18 °C?
Dauer: [1] h
d) Lies den Wert $T(9)$ ab!
Ergebnis: [1]
e) Für welche Uhrzeiten $t$ gilt $T(t) = 13$?
Ergebnis: [0]
f) Zu welcher Uhrzeit wurde das Temperaturmaximum erreicht? Das Ergebnis soll maximal 30 Minuten vom tatsächlichen Wert abweichen.
Uhrzeit: [0]
#861 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Fehler melden
Der Geschwindigkeitsverlauf eines Formel-1-Autos während einer Runde ist durch folgenden Funktionsgraphen gegeben, wobei auf der vertikalen Achse die Geschwindigkeit (in km/h) und auf der horizontalen Achse die Zeit (in s) aufgetragen wurde.
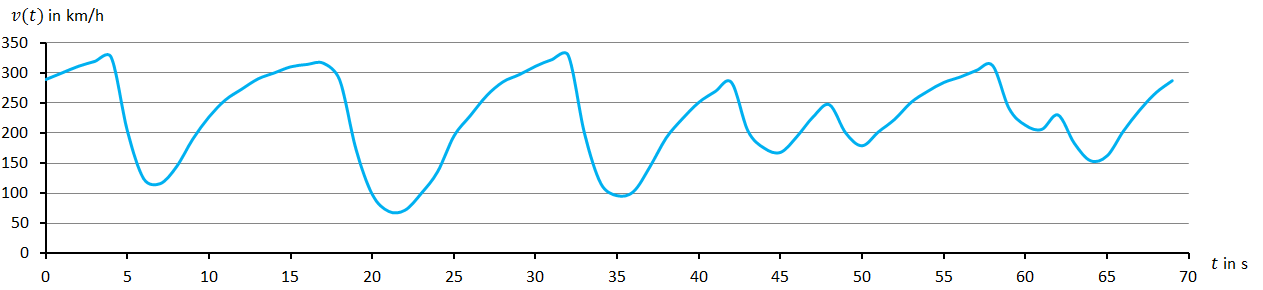
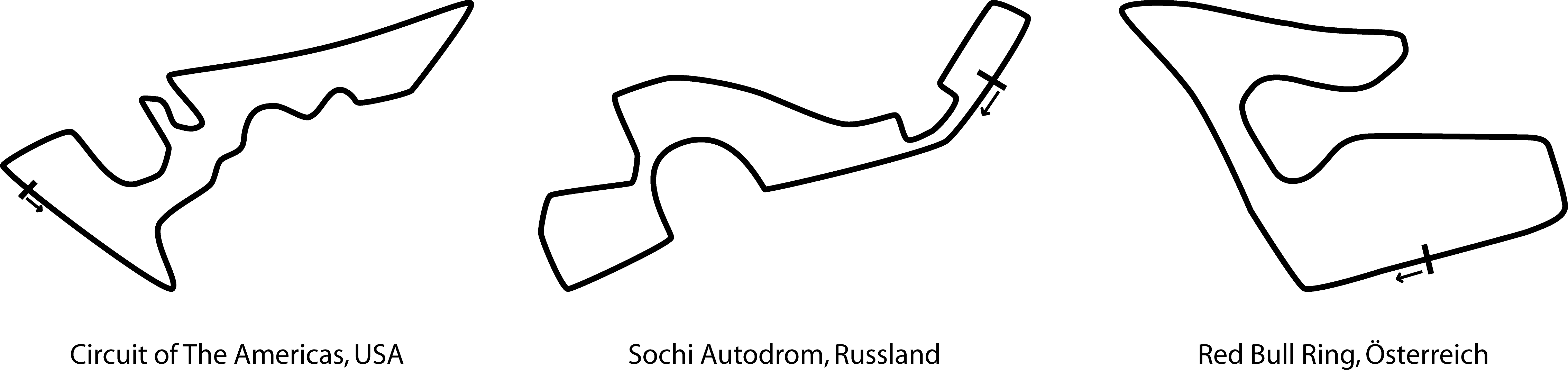
Argumentiere, zu welcher der drei abgebildeten Rennstrecken dieses Diagramm am besten passt.
0/1000 Zeichen
#1097 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Fehler melden
Gib an, ob die folgenden Aussagen wahr oder falsch sind.
Es gibt Funktionen, für die $f(1)=3$ und $f(5)=3$ gilt.
Es gibt Funktionen, für die $f(1)=3$ und $f(1)=5$ gilt.
Der Ordinatenabschnitt von $f(x)=(x+3)^2+5$ ist 5.
Der Punkt $(\,2 \mid 5\,)$ liegt am Graphen der Funktion $f(x)=2x−1$.
Die Funktion $f(x)=3x^2−9x−30$ hat bei $x=5$ eine Nullstelle.
Die Funktion $f(x)=2^x$ besitzt keine Nullstellen.#1323 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Fehler melden
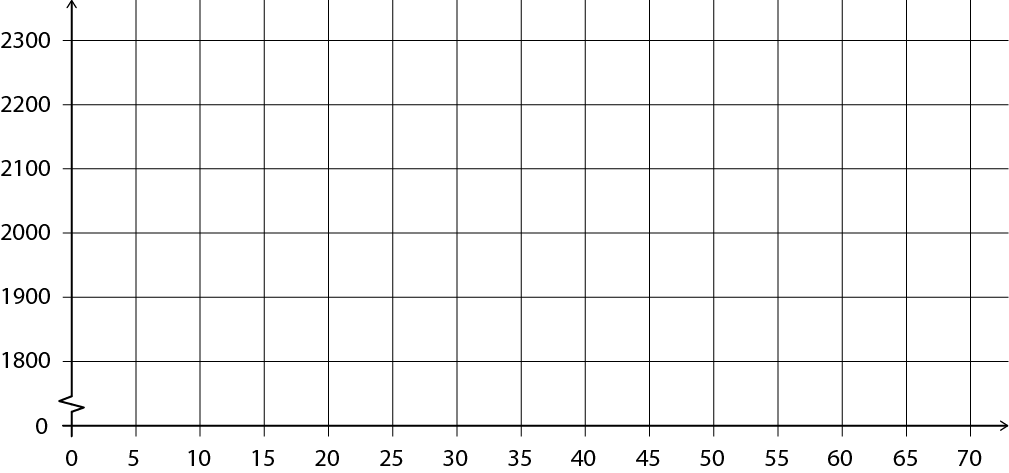
Erkläre, was im nachfolgenden Koordinatensystem die Zacken im unteren Bereich der vertikalen Achse bedeuten.
0/1000 Zeichen
#1340 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Fehler melden
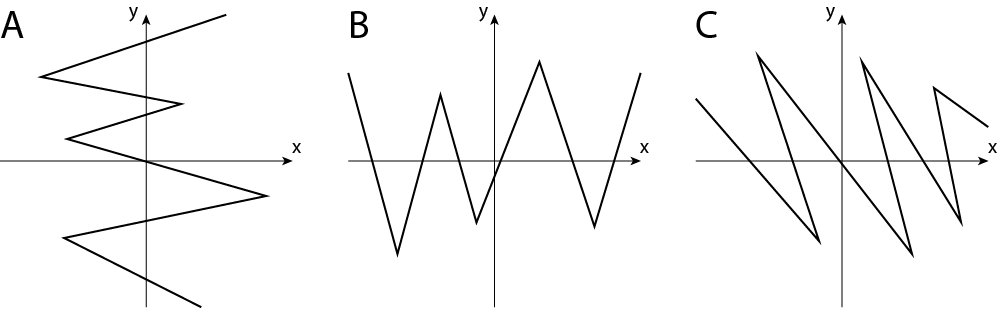
Erkläre möglichst ausführlich, ob es sich bei den folgenden Abbildungen um einen Funktionsgraphen handelt oder nicht.
Abbildung A:
0/1000 Zeichen Abbildung B:
0/1000 Zeichen Abbildung C:
0/1000 Zeichen
#1341 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Fehler melden
Es ist die Funktionsgleichung $f(x)=2.8-0.23x^2$ gegeben.
a) Fülle die nachfolgende Wertetabelle aus.
| $x$ | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| $f(x)$ |
#1342 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Fehler melden
Nachfolgend ist der Graph einer Funktion abgebildet.
a) Ergänze die folgenden Werte:
$f(2)=\,$ [1]
$f(x)=1 $ ist erfüllt für $x=\,$ [1]
b) Bestimme die Nullstelle und den Ordinatenabschnitt ($y$-Achsenabschnitt).
Nullstelle: [1]
Ordinatenabschnitt : [1]
c) Die Funktion ist streng monoton .
#1343 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Fehler melden
Der Kontostand einer Person wird durch die Funktion $K(x)$ beschrieben, wobei die Variable $x$ für die Anzahl der Tage beginnend beim heutigen Tag steht. Erkläre jeweils möglichst präzise, was durch die folgenden Ausdrücke beschrieben wird.
a) $K(6)>K(3)$
0/1000 Zeichen b) $K(28)=K(27)+344.69$
0/1000 Zeichen b) $K(17)=1421.11$
0/1000 Zeichen
#1374 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Fehler melden
Die nachfolgende Abbildung zeigt die Entwicklung einer Aktie innerhalb von 14 Tagen.
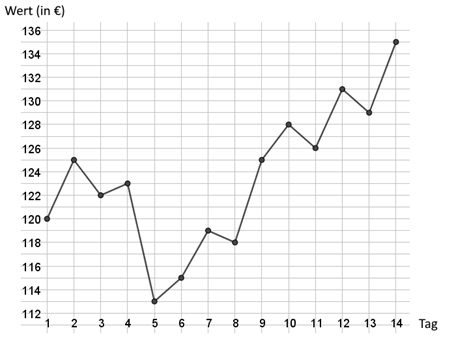
Vervollständige den Lückentext: Von Tag 4 auf Tag 5 ist der Wert um [0] € gefallen und erreichte damit das Minimum von [0] €. Der größte Anstieg innerhalb eines Tages ereignete sich von Tag [0] auf Tag [0]. An Tag [0] betrug der Wert der Aktie exakt 128 €. Innerhalb des gesamten Zeitraums ist der Wert um [0] € gestiegen, das sind [1] % des Anfangswertes.
2. Funktionen modellieren
#113 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Fehler melden
Nachfolgend ist der Graph einer quadratischen Funktion abgebildet. Erstelle die zugehörige Funktionsgleichung in Polynomform $f(x)=ax^2+bx+c$. Es ist sinnvoll, diese zuerst in Scheitelpunktform zu erstellen und anschließend umzurechnen.
$a=$ [0]
$b=$ [0]
$c=$ [0]
#120 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Fehler melden
Nachfolgend ist der Graph einer Potenzfunktion abgebildet. Erstelle die zugehörige Funktionsgleichung $f(x)=a\cdot (x+h)^n+v$. Für $n$ kommen nur ganzzahlige Werte von inklusive $-2$ bis inklusive $3$ in Frage.
$a=$ [0]
$h=$ [0]
$n=$ [0]
$v=$ [0]
#122 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Fehler melden
Bestimme für die beiden abgebildeten Funktionsgraphen eine Funktionsgleichung im Format $f(x)=c\cdot a^x$. Suche dazu möglichst gut ablesbare Punkte des Funktionsgraphen.
Blauer Funktionsgraph (ansteigend): $\,f(x)=$ [2]
Roter Funktionsgraph (abfallend): $\,g(x)=$ [2]
#519 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Fehler melden
Der nachfolgende Funktionsgraph soll durch die Funktionsgleichung $f(x)=A\cdot \cos(2\pi \cdot \omega \cdot x)+d$ beschrieben werden. Bestimme die Parameter $A$, $\omega$ und $d$.
$A=\,$ [0]
$\omega=\,$ [3]
$d=\,$ [0]
#552 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Fehler melden
Gib die Funktionsgleichung einer Exponentialfunktion in der Form $f(x)=c\cdot a^x$ an, die dem unten abgebildeten Funktionsgraphen entspricht.
Funktionsgleichung: [0]
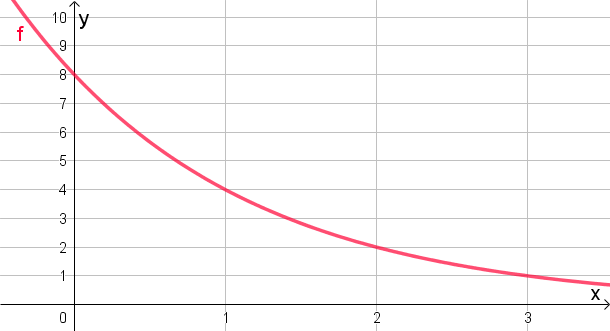
#638 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Fehler melden
Bestimme die Funktionsgleichung des abgebildeten Funktionsgraphen. Gib einen vollständigen Lösungsweg an.
Funktionsgleichung (inkl. Lösungsweg):
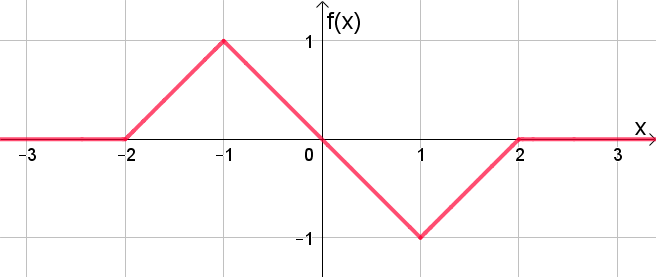
#658 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Fehler melden
Ergänze die Lücken der Funktionsterme und achte dabei auf die vorgegebenen Vorzeichen.
a) Blauer Graph: $~f(x)=-0.3\cdot(x-\,\_\_\_\_\_\,)\cdot(x+\,\_\_\_\_\_\,)$
1. Lücke: [0]
2. Lücke: [0]
b) Roter Graph: $~g(x)=-0.2 \cdot(x-\,\_\_\_\_\_\,)^2+\,\_\_\_\_\_$
1. Lücke: [0]
2. Lücke: [0]
c) Grüner Graph: $~h(x)=0.3x^2-1.4x+\,\_\_\_\_\_$
Lücke: [0]
#1216 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Fehler melden
Nachfolgend sind drei Funktionsgraphen von linearen Funktionen abgebildet. Ermittle jeweils die zugehörige Funktionsgleichung.
Blauer Funktionsgraph: $f(x)=$ [0]
Roter Funktionsgraph: $g(x)=$ [0]
Grüner Funktionsgraph: $h(x)=$ [0]
#1264 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Fehler melden
Bestimme die Parameter $b$, $c$ und $k$ der Funktion $N(t)=c\cdot \left(1- e^{-k\cdot t} \right)+b$ so, dass der Funktionsgraph deiner Funktion in den wesentlichen Bereichen mit der folgenden Abbildung übereinstimmt.
$b=$ [0]
$c=$ [0]
$k=$ [3]
#1265 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Fehler melden
Bestimme die Parameter $S$, $c$ und $a$ der logistischen Funktion $N(t)=\frac{S}{1+c\cdot a^t}$ so, dass der Funktionsgraph deiner Funktion in den wesentlichen Bereichen mit der folgenden Abbildung übereinstimmt.
$S=$ [0]
$c=$ [3]
$a=$ [3]
3. Funktionstransformation
#185 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Fehler melden
Nachfolgend ist der Graph der Funktion $f(x)=\frac{1}{x^2+1}$ abgebildet. Dieser Graph soll um 4 nach rechts verschoben und vertikal um den Faktor 3 gestreckt werden.
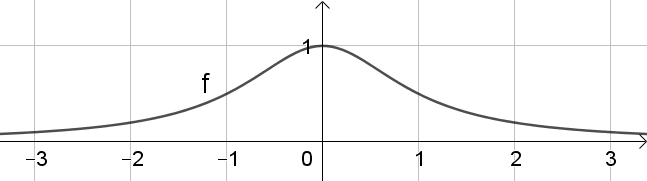
a) Zeichne den neuen Funktionsgraph in ein Koordinatensystem mit Koordinatengitter und beschrifteten Achsen.
Funktionsgraph:
b) Ermittle die Funktionsgleichung der neuen Funktion. Im Ergebnis sollen keine Klammern vorkommen. Gib alle Rechenschritte an.
Funktionsgleichung (inkl. Rechenweg):
#1096 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Fehler melden
Gib an, ob die folgenden Aussagen wahr oder falsch sind.
Der Graph von $g(x) = f(x + 5)$ ist im Vergleich zu jenem der Funktion $f$ um 5 nach rechts verschoben.
Der Graph von $g(x) = f(x - 3)$ ist im Vergleich zu jenem der Funktion $f$ um 3 nach rechts verschoben.
Der Graph von $g(x) = f(x) + 2$ ist im Vergleich zu jenem der Funktion $f$ um 2 nach oben verschoben.
Der Graph von $g(x)=f(x+3)$ ist im Vergleich zu jenem der Funktion $f$ um 3 nach links verschoben.4. Vermischte Aufgaben
#216 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Fehler melden
Gib an, ob die folgenden Aussagen zu geraden und ungeraden Funktionen wahr oder falsch sind.
Es gibt eine Funktion, die gerade und ungerade zugleich ist.
Es gibt Funktionen, die weder gerade noch ungerade sind.
Eine Polynomfunktion mit ausschließlich geraden Exponenten ist immer gerade.
Eine Polynomfunktion mit ausschließlich ungerade Exponenten ist immer ungerade.
Der Funktionsgraph jeder ungeraden Funktion verläuft durch den Koordinatenursprung.
Multipliziert man eine gerade Funktion mit einer geraden Funktion, so ist das Ergebnis ebenfalls eine gerade Funktion.
Multipliziert man eine ungerade Funktion mit einer ungeraden Funktion, so ist das Ergebnis ebenfalls eine ungerade Funktion.
Multipliziert man eine ungerade Funktion mit einer ungeraden Funktion, so ist das Ergebnis eine gerade Funktion.
Multipliziert man eine ungerade Funktion mit einer geraden Funktion, so ist das Ergebnis immer eine ungerade Funktion.#318 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Fehler melden
Wie viele Schnittpunkte haben die Funktionen $f(x) = x^2$ und $g(x) = 2^x$?
Ergebnis: [0]#1149 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Fehler melden
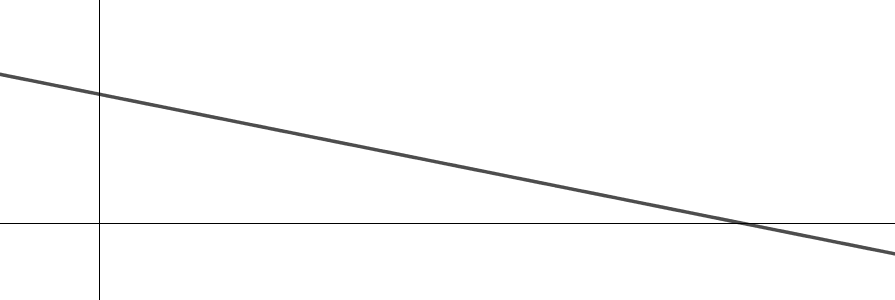
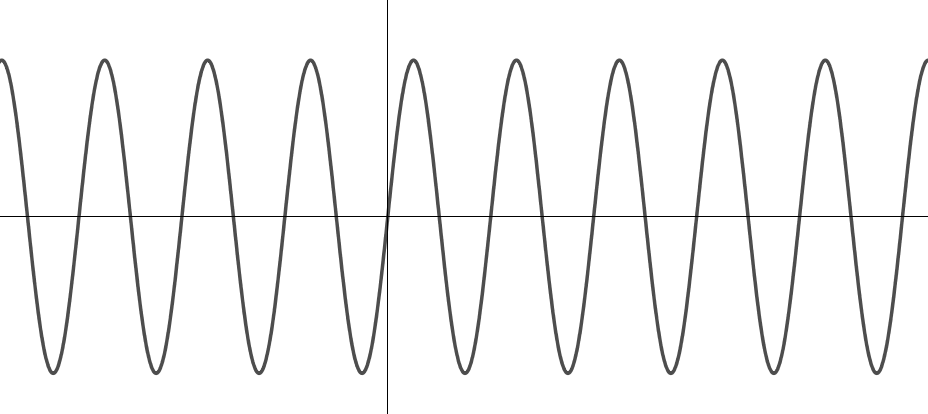
Wähle jeweils aus, um welchen Funktionstyp es sich handelt.
Urheberrechtshinweis: Die auf dieser Seite aufgelisteten Aufgaben unterliegen dem Urheberrecht (siehe Impressum). |