Aufgaben zu Exponentialfunktionen
Dieser Bereich der Website befindet sich im Umbau.
Betrachten Sie daher auch folgende Arbeitsblätter für mehr Aufgaben zu diesem Thema:
1. Exponentialfunktion
Wandle die vorgegebene Funktion jeweils in eine Darstellung mit der vorgegebenen Basis um!
a) f(x)=7.3x in f(x)=4.9k⋅x
b) g(x)=1.652x in g(x)=ek⋅x
#122 |
Lösung anzeigen · Einzelansicht · Aufgabe neu generieren · Fehler melden
Bestimme für die beiden abgebildeten Funktionsgraphen eine Funktionsgleichung im Format f(x)=c⋅ax. Suche dazu möglichst gut ablesbare Punkte des Funktionsgraphen.

#334 |
keine Lösung vorhanden · Einzelansicht · Aufgabe neu generieren · Fehler melden
Gegeben ist die Funktion f(x)=5⋅2x. Gib an, ob die folgenden Aussagen wahr oder falsch sind.
Wird x um 2 vergrößert, so verdoppelt sich der Funktionswert.
Wird x um 1 vergrößert, so steigt der Funktionswert um 100 %.
Wird die Variable x um 1 vergrößert, so verfünffacht sich der Funktionswert.
Der Funktionsgraph schneidet die senkrechte Achse beim Wert 5.
Wird x um 2 verkleinert, so sinkt der Funktionswert auf ein Viertel des ursprünglichen Werts.
Im Intervall [2,3] ist die Funktion um denselben absoluten Wert angestiegen, wie im Intervall [3,4].
Verkleinert man x um 1, so sinkt der Funktionswert um 50 %.#552 |
keine Lösung vorhanden · Einzelansicht · Aufgabe neu generieren · Fehler melden
Gib die Funktionsgleichung einer Exponentialfunktion in der Form f(x)=c⋅ax an, die dem unten abgebildeten Funktionsgraphen entspricht.
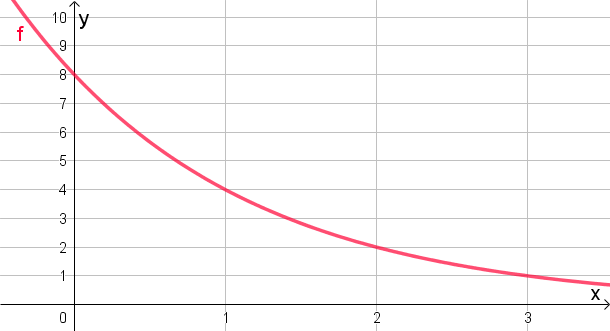
#562 |
keine Lösung vorhanden · Einzelansicht · Aufgabe neu generieren · Fehler melden
Kreuze an, ob es sich um eine exponentielle Zunahme oder Abnahme handelt.
f(x)=20⋅50.5x
f(x)=5⋅e−0.3x
f(x)=0.4⋅3x
f(x)=3⋅e0.1x
f(x)=7⋅0.12x#563 |
keine Lösung vorhanden · Einzelansicht · Aufgabe neu generieren · Fehler melden
Im folgenden Koordinatensystem sind die Graphen der Exponentialfunktionen f(x)=c⋅ax und g(x)=d⋅bx eingezeichnet. Kreuze alle Aussagen an, die auf diese beiden Funktionen zutreffen.
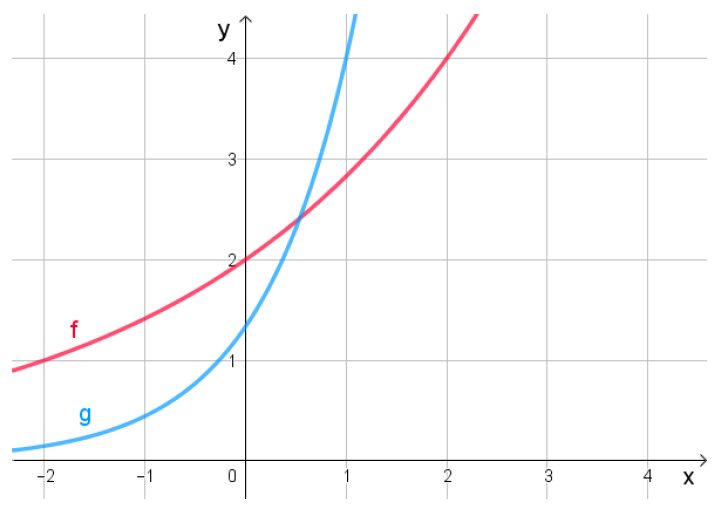
#693 |
keine Lösung vorhanden · Einzelansicht · Aufgabe neu generieren · Fehler melden
Eine Exponentialfunktion der Form f(x)=c⋅ax soll durch die Punkte (x1∣y1) und (x2∣y2) verlaufen. Erstelle allgemein anwendbare Formeln zur Berechnung von a und c. Die Formeln dürfen nur die Koordinaten der Punkte enthalten und sollen möglichst weit vereinfacht sein.
#1020 |
Lösung anzeigen · Einzelansicht · Aufgabe neu generieren · Fehler melden
Gegeben ist die Exponentialfunktion f(x)=2.9⋅1.38x. Vervollständige den Lückentext!
▪
Der Funktionsgraph schneidet die Ordinate (y-Achse) beim Wert _______________ . ▪
Wird x um 2 verkleinert, so sinkt der Funktionswert auf _______________ % des ursprünglichen Werts. ▪
Wird x um 12 vergrößert, so steigt der Funktionswert um _______________ %. ▪
An der Stelle 3.9 beträgt der Funktionswert _______________ . ▪
Den Wert 41 erreicht die Funktion an der Stelle _______________ .#1104 |
keine Lösung vorhanden · Einzelansicht · Aufgabe neu generieren · Fehler melden
Gib an, ob die folgenden Aussagen wahr oder falsch sind.
Die Funktionen f(x)=ax und g(x)=a−x sind bezüglich der y-Achse gespiegelt.
Der Graph der Funktion f(x)=c⋅ax verläuft durch den Punkt (0∣c).
Die Graphen von f(x)=5⋅3x und g(x)=3⋅2x haben keinen Schnittpunkt.
Zwei verschiedene Exponentialfunktionen der Form f(x)=c⋅ax haben immer genau einen Schnittpunkt.
Eine Exponentialfunktion der Form f(x)=c⋅ax hat niemals eine Nullstelle.2. Lineare Funktion vs. Exponentialfunktion
#326 |
Lösung anzeigen · Einzelansicht · Aufgabe neu generieren · Fehler melden
Im Jahr 2000 hatte Mexiko 100,35 Mio. Einwohner. Zehn Jahre später waren es 112,32 Mio. Einwohner.
a) Wie viele Menschen leben unter der Annahme eines linearen Bevölkerungswachstums voraussichtlich im Jahr 2068 in Mexiko?
b) Wie viele Menschen leben unter der Annahme eines exponentiellen Bevölkerungswachstums voraussichtlich im Jahr 2068 in Mexiko?
#335 |
keine Lösung vorhanden · Einzelansicht · Aufgabe neu generieren · Fehler melden
Gib jeweils an, ob es sich um einen linearen oder um einen exponentiellen Zusammenhang handelt.
Das Taschengeld wird jährlich um 10 Euro erhöht.
Die Bakterienkultur wächst alle 20 Minuten um 10 %.
Das Kapital wird jedes Quartal mit 0,5 % verzinst.
Der Wasserstand sinkt nach jeweils 15 Minuten um 5 cm.
Die Umfragewerte einer Partei stiegen heuer pro Monat um 2 Prozentpunkte.#549 |
keine Lösung vorhanden · Einzelansicht · Aufgabe neu generieren · Fehler melden
Gib jeweils an, ob es sich um ein lineares oder um ein exponentielles Bevölkerungswachstum handelt.
Die Bevölkerung wächst jährlich um ca. 50 000 Einwohner.
Die Bevölkerung wächst jährlich um ca. 1,3 %.
Die Bevölkerung verdoppelt sich alle 70 Jahre.
Pro Jahrhundert steigt die Bevölkerung um ca. 1 Mio. Einwohner.#553 |
keine Lösung vorhanden · Einzelansicht · Aufgabe neu generieren · Fehler melden
Gib jeweils an, ob es sich um einen linearen oder um einen exponentiellen Zusammenhang handelt.
Der Umsatz eines Unternehmens steigt pro Jahr um 20 %.
Ein menschliches Haar wächst pro Tag um 0,05 mm.
Der Wasserstand der Donau steigt pro Stunde um 2 cm.
Die Anzahl an Bakterien verdreifacht sich alle fünf Stunden.#572 |
keine Lösung vorhanden · Einzelansicht · Aufgabe neu generieren · Fehler melden
Nachfolgend sind drei Wertetabellen gegeben. Gib jeweils an, ob es sich hier um eine lineare Abnahme, ein lineares Wachstum, eine exponentielle Abnahme oder ein exponentielles Wachstum handelt und begründe, woran man das erkennen kann.
| x | 0 | 1 | 2 | 3 |
| f(x) | 0,2 | 0,6 | 1,8 | 5,4 |
| x | 0 | 1 | 2 | 3 |
| f(x) | 0,7 | 2,0 | 3,3 | 4,6 |
| x | 0 | 1 | 2 | 3 |
| f(x) | 5,0 | 2,5 | 1,25 | 0,625 |
#1029 |
keine Lösung vorhanden · Einzelansicht · Aufgabe neu generieren · Fehler melden
Nachfolgend sind für vier Länder die Wachstumsfunktionen der Einwohnerzahlen gegeben. Dabei ist E(t) die Einwohnerzahl (gemessen in Millionen Einwohnern) und t die Zeit (gemessen in Jahren ab 2000). Beschreibe jeweils anhand eines vollständigen Satzes, wie sich die Einwohnerzahl gemäß dieser Funktionen jährlich verändert!
a) E(t)=40.2⋅1.0153t
b) E(t)=1.27t+76.7
c) E(t)=23.8
d) E(t)=22.1⋅0.9831t
3. Vermischte Aufgaben
#356 |
Lösung anzeigen · Einzelansicht · Aufgabe neu generieren · Fehler melden
Ein Blatt Papier kann nur ca. sieben Mal in der Mitte gefaltet werden. Je nach Art des Papiers kann es kleine Abweichungen geben.
a) Wie oft müsste man ein 0.17 mm dickes Blatt Papier mindestens falten, damit der entstehende „Turm“ höher als 1 m ist?
b) Wie dick wäre der „Turm“, wenn das Blatt 45 Mal gefaltet wird?
c) Recherchiere im Internet nach einer vergleichbaren Größe aus der Realität, um sich das Ergebnis von Aufgabe b) besser vorstellen zu können.
#361 |
Lösung anzeigen · Einzelansicht · Aufgabe neu generieren · Fehler melden
Von einem bestimmten Medikament werden im Körper pro Stunde 13 % der noch vorhandenen Menge abgebaut.
a) Berechne die Halbwertszeit dieses Medikaments.
b) Stelle den Abbauvorhang grafisch dar. Gehe davon aus, dass zum Zeitpunkt t=0 noch 100 % des Medikaments im Körper waren.
#486 |
keine Lösung vorhanden · Einzelansicht · Aufgabe neu generieren · Fehler melden
Erstelle für die folgenden Sachverhalte jeweils eine geeignete Funktionsgleichung. Verwende für den Anfangswert die Bezeichnung f(x) und für die unabhängige Variable die Bezeichnung x.
a) Alle 3 Jahre wächst die Bevölkerung einer Stadt um 2200 Einwohner (x gemessen in Jahren).
b) Die Lichtintensität nimmt in einem See pro Meter um 14.3 % ab (x gemessen in Metern).
c) Eine Bakterienkultur verdoppelt sich alle 4 Stunden (x gemessen in Stunden).
#561 |
Lösung anzeigen · Einzelansicht · Aufgabe neu generieren · Fehler melden
Es sollen 4800 € zu einem fixen jährlichen Zinssatz angelegt werden. Wie groß müsste dieser Zinssatz sein, damit nach 11 Jahren 7900 € vorhanden sind?
#747 |
Lösung anzeigen · Einzelansicht · Aufgabe neu generieren · Fehler melden
In einem bestimmten See halbiert sich die Intensität des Sonnenlichts unterhalb der Wasseroberfläche nach jeweils 5 m. Welcher Anteil des Sonnenlichts erreicht den Grund des Sees in 30 m Tiefe?
© 2016 – 2025 MATHE.ZONE