Polynomform
Die Polynomform ist aufgrund ihrer kompakten Form (keine Klammern) sehr häufig anzutreffen. Sie hat folgende allgemeine Struktur: f(x)=a⋅x2+b⋅x+c.
In diesem Abschnitt wird die Bedeutung der drei Parameter a,b,c ausführlich behandelt.
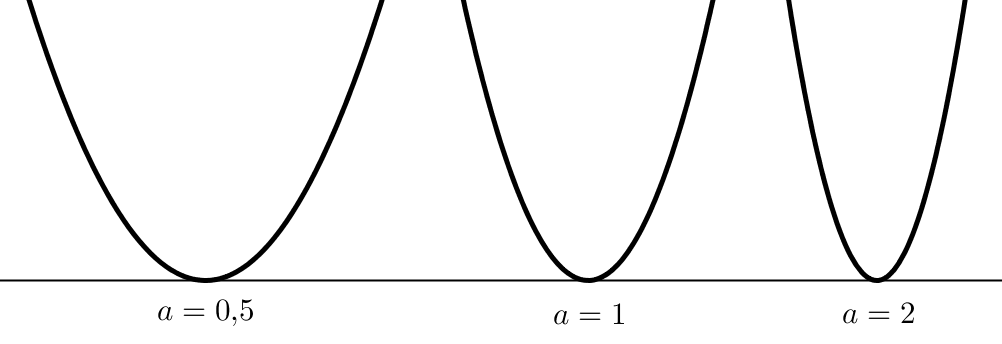
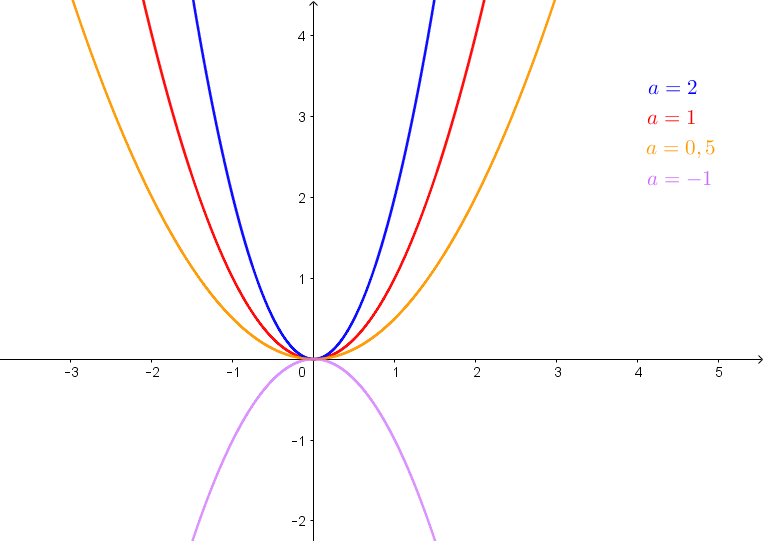
Außerdem gibt der Betrag von a Auskunft darüber, wie spitz die Parabel ist. Je größer |a| ist, umso größer ist die Krümmung betragsmäßig und umso spitzer ist dementsprechend die Parabel.
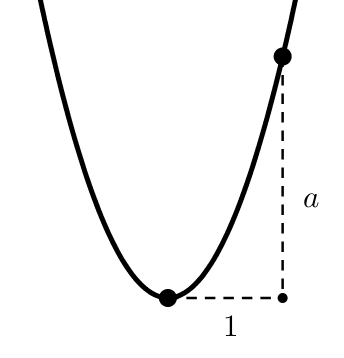
Man kann den Parameter a direkt aus dem Funktionsgraphen ablesen. Dazu markiert man den Scheitelpunkt und geht von diesem um 1 nach rechts. Von dort geht man nun so weit nach oben bzw. unten, bis der Funktionsgraph erreicht wird. Der vertikale Abstand entspricht dem Parameter a. Ging man nach oben, so ist a positiv. Ging man nach unten, so ist a negativ.
Parameter a (Krümmung)
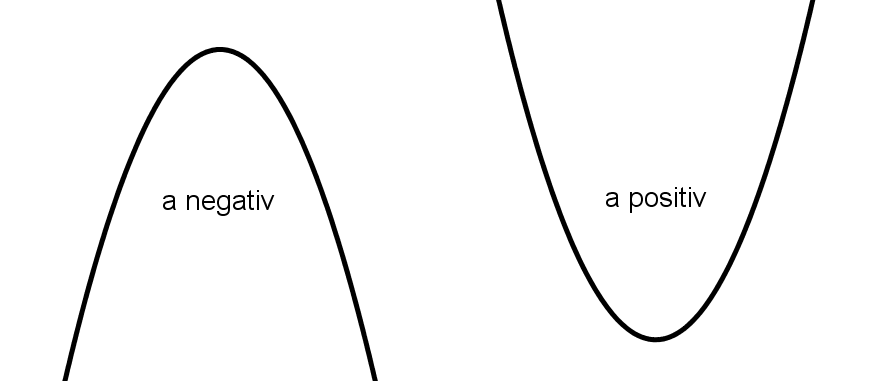
Der Parameter a, welcher als einziger Parameter in allen drei Darstellungsformen (Polynomform, Scheitelpunktform, Nullstellenform) vorkommt, ist ein Maß für die Krümmung der Parabel. Je nach Vorzeichen von a ist die Parabel entweder nach oben geöffnet (positive Krümmung) oder nach unten geöffnet (negative Krümmung).


- Ist a>0, so ist die Parabel nach oben geöffnet (positiv gekrümmt).
- Ist a<0, so ist die Parabel nach unten geöffnet (negativ gekrümmt).
- Je größer der Betrag von a ist, umso steiler/spitzer ist die Parabel.
- Je kleiner der Betrag von a ist, umso flacher ist die Parabel.


Herleitung
Um die oben beschriebene Vorgehensweise zu begründen, müssen die Funktionswerte an der Stelle des Scheitelpunkts und 1 rechts davon berechnet und verglichen werden. Dazu wird die Scheitelpunktform f(x)=a⋅(x−xS)2+yS verwendet.
Setzt man xS, also die x-Koordinate des Scheitelpunkts, ein, so erhält man f(xS)=a⋅(xS−xS)2+yS=a⋅02+yS=yS. Setzt man xS+1 ein, so erhält man f(xS+1)=a⋅(xS+1−xS)2+yS=a⋅12+yS=a+yS.
Man erkennt, dass der vertikale Abstand zwischen diesen Punkten genau a beträgt.
Beispiel 1
Es soll eine Funktionsgleichung erstellt werden, welche dem nachfolgend abgebildeten Funktionsgraphen entspricht.
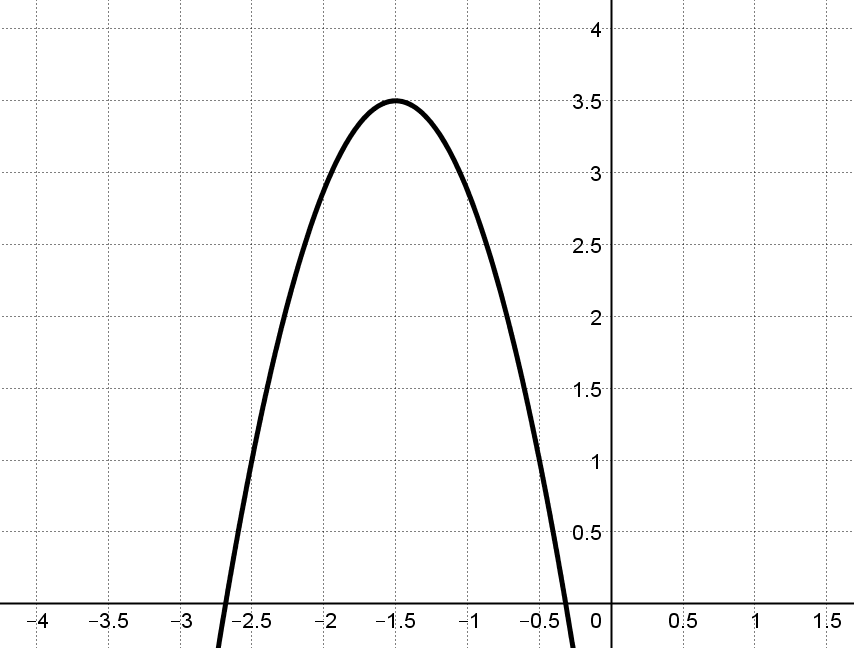
Der Scheitelpunkt befindet sich bei den Koordinaten (−1,5∣3,5). Geht man von diesem aus um 1 nach rechts, so muss man 2,5 nach unten gehen, um den Graph zu erreichen. Daher ist der Parameter a=−2,5. Die vollständige Funktionsgleichung in Scheitelpunktform lautet somit f(x)=−2,5⋅(x+1,5)2+3,5.

Aufgabe 1
Löse die folgende Aufgabe: 5@quadratische-funktionen
Parameter b (Ordinatensteigung, Symmetrie)
Der Parameter b entspricht der Steigung, mit welcher die Parabel die y-Achse (Ordinate) schneidet.
Begründung
Für diese Begründung werden Kenntnisse der Differentialrechnung vorausgesetzt (ansonsten überspringen). Bildet man von der Funktionsgleichung f(x)=ax2+bx+c die Ableitungsfunktion, so erhält man f′(x)=2ax+b. Die Ableitungsfunktion f′ gibt an, welche Steigung die Funktion f an der Stelle x besitzt. Setzt man x=0, so erhält man f′(0)=2a⋅0+b=b. Daher wird die y-Achse mit der Steigung b geschnitten.
In der folgenden Grafik sieht man drei Parabeln. Die blaue Parabel geht bei der y-Achse nach unten (daher ist b hier negativ), die gelbe Parabel geht nach oben (daher ist b hier positiv) und die rote Parabel verläuft bei der y-Achse waagrecht (daher ist b hier 0).
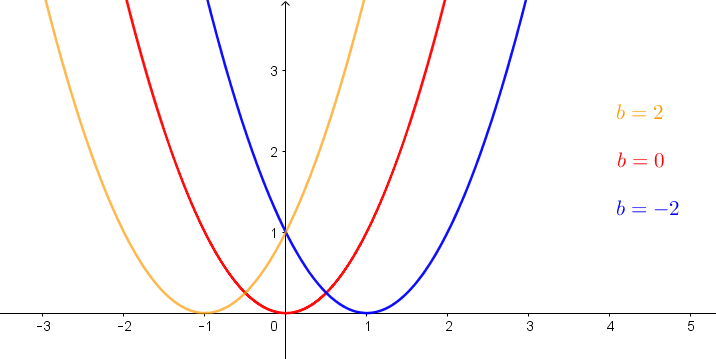
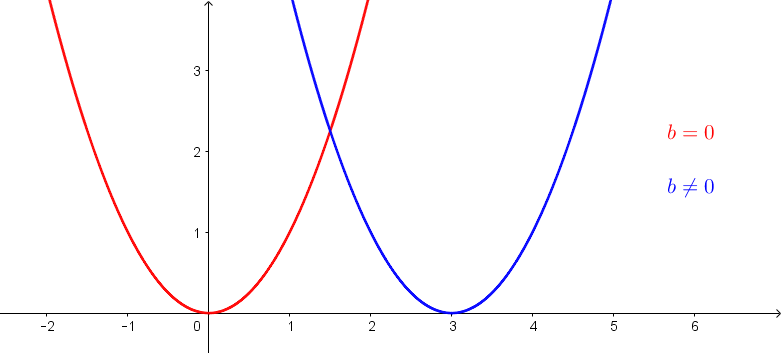
WICHTIG: Anhand des Parameters b kann man auch erkennen, ob die Parabel symmetrisch zur y-Achse ist. Ist b=0, so befindet sich der Scheitelpunkt direkt auf der y-Achse und somit ist der Funktionsgraph symmetrisch zur y-Achse.


Parameter c (Ordinatenabschnitt)
Der Ordinatenabschnitt ist jener Funktionswert, bei welchem der Funktionsgraph die vertikale Achse (auch Ordinate genannt; daher die Bezeichnung Ordinatenabschnitt) schneidet. Man spricht daher auch vom y-Achsenabschnitt. Häufig handelt es sich bei anwendungsbezogenen Aufgaben um den Startwert (z. B. die Fixkosten oder die Abwurfhöhe).
Man kann diesen Wert bestimmen, indem man f(0) berechnet.
Beispiel 2
Es soll der Ordinatenabschnitt der Funktion f(x)=−2⋅(x−3)2+5 berechnet werden. Setzt man x=0 in die Funktionsgleichung ein, so erhält man f(0)=−2⋅(0−3)2+5=−13. Somit ist der Ordinatenabschnitt −13 was bedeutet, dass die y-Achse bei −13 geschnitten wird.
Ist der Ordinatenabschnitt 0, so verläuft der Funktionsgraph durch den Ursprung des Koordinatensystems. Man bezeichnet eine derartige quadratische Funktion als homogen.
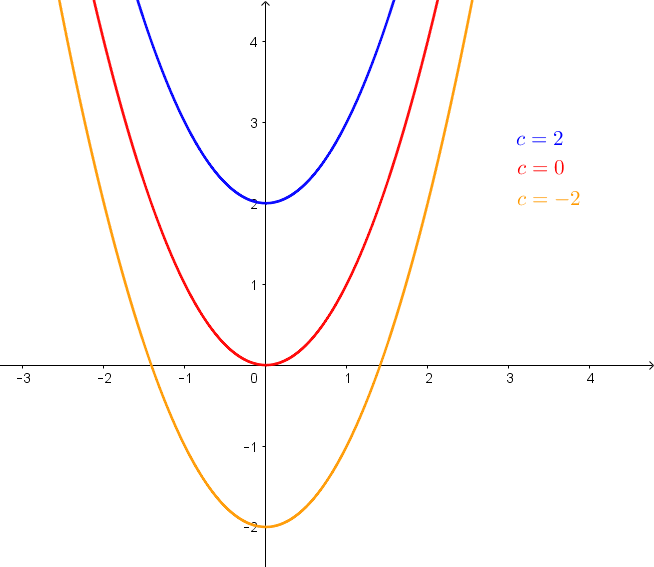
- Ist c>0, so wird die y-Achse im positiven Bereich geschnitten.
- Ist c=0, so wird die y-Achse im Koordinatenursprung geschnitten.
- Ist c<0, so wird die y-Achse im negativen Bereich geschnitten.

Aufgabe 2
Löse die folgende Aufgabe: 16@quadratische-funktionen
Feedback
Wie hilfreich war dieses Kapitel für dich?
© 2016 – 2025 MATHE.ZONE