Nullstellenform | Funktionsgleichung mittels Punkten bestimmen

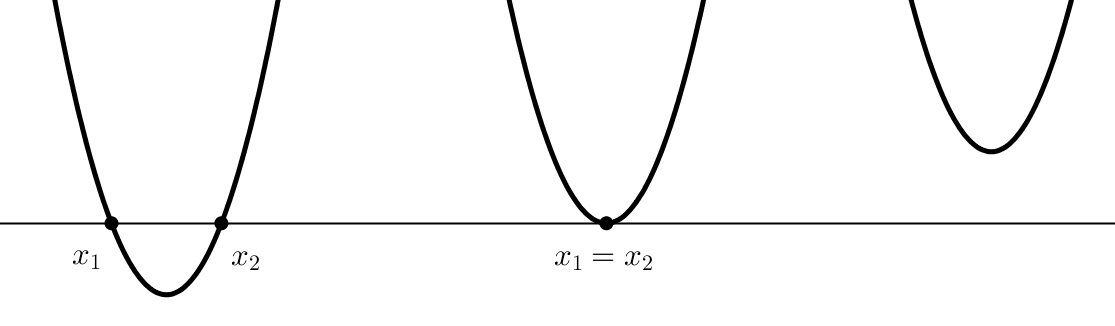
Die Parameter $x_1$ und $x_2$ repräsentieren die Nullstellen der quadratischen Funktion, also jene Stellen, an denen der Funktionsgraph die $x$-Achse schneidet. Es gibt entweder zwei, eine oder keine Nullstellen (siehe Abbildung oben). Um die Nullstellen einer quadratischen Funktion zu bestimmen, wird die Gleichung $f(x)=0$ nach $x$ aufgelöst, da sich die Nullstellen dort befinden, wo der Funktionswert 0 ist. Je nachdem, welche Darstellungsform der Funktionsgleichung vorliegt, sieht die Berechnung unterschiedlich aus. Ist die Funktionsgleichung in Polynomform gegeben, so erfolgt die Berechnung mittels der Lösungsformel für quadratische Gleichungen: $$x_{1,2}=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$

Es sollen die Nullstellen der quadratischen Funktion $f(x)=3x^2 - 21x + 30$ berechnet werden. Dazu muss die Gleichung $0=3x^2 - 21x + 30$ gelöst werden. Hierfür werden die Koeffizienten in die Lösungsformel für quadratische Gleichungen eingesetzt. Man erhält folgendes Resultat: $$x_{1,2}=\frac{21\pm \sqrt{21^2-4\cdot 3\cdot 30}}{2\cdot 3}=\frac{21\pm 9}{6}~~\Rightarrow~~ x_1=5\text{ und }x_2=2$$ Die Nullstellen befinden sich an den Stellen 2 und 5.

Öffne das Arbeitsblatt: https://mathe.zone/data/arbeitsblaetter/quadratische-funktionen.pdf Löse die Aufgaben 6 a,b,c,d,e,f,g,h,i,j,n,o,p und vergleiche deine Ergebnisse mit den Lösungen.

Ist der Term $b^2-4ac$ negativ, so kann die in der Lösungsformel vorkommende Quadratwurzel nicht berechnet werden. Somit gibt es keine Lösung und die quadratische Funktion hat daher keine Nullstellen. Falls $b^2-4ac=0$, erfüllt ist, fällt die Wurzel in der Lösungsformel weg und es gibt daher nur eine einzige Lösung. Dies bedeutet, dass die quadratische Funktion nur eine einzige Nullstelle besitzt, welche zugleich dem Scheitelpunkt entspricht.

Löse die folgende Aufgabe: 8@quadratische-funktionen

Finde jeweils eine Funktionsgleichung in Polynomform, die a) zwei Nullstellen, b) eine Nullstelle, c) keine Nullstelle besitzt. Beschreibe deine Vorgehensweise.

Ist die Funktionsgleichung in Scheitelpunktform gegeben, so kann die entsprechende Gleichung durch Umformung gelöst werden, da hier nur ein einziges $x$ vorkommt.

Es sollen die Nullstellen der quadratischen Funktion $f(x)=2\cdot (x-4)^2-8$ berechnet werden. Dadurch wird auf der linken Seite für den Funktionswert 0 eingesetzt und nach $x$ aufgelöst: \begin{align} 0 &= 2\cdot (x-4)^2-8 \\ 8 &= 2\cdot(x-4)^2 \\ 4 &= (x-4)^2 \mid \mathrm{Wurzel~ziehen~(dadurch~entstehen~zwei~Lösungen)}\\ \pm 2 &=x-4 \\ x &= 4 \pm 2\\ x_1 &= 6,~~x_2=2 \end{align} Die beiden Nullstellen befinden sich also bei 2 und 6.

Berechne die Nullstellen von $f(x)=-\frac{1}{2}\cdot (x-3)^2+4$. Lösungen: 0,172 und 5,828

Löse die folgende Aufgabe: 6@quadratische-funktionen

Finde jeweils eine Funktionsgleichung in Scheitelpunktform, die a) zwei Nullstellen, b) eine Nullstelle, c) keine Nullstelle besitzt. Beschreibe deine Vorgehensweise.

Aus der Nullstellenform können die Nullstellen direkt ohne Rechnung abgelesen werden. Es ist dabei jedoch auf das Vorzeichen zu achten, da die Nullstellenform grundsätzlich negative Vorzeichen enthält.

Es sollen die Nullstellen der quadratischen Funktion $f(x)=5\cdot (x-1)\cdot (x+4)$ bestimmt werden. Die erste Nullstelle lautet $x_1=1$ und die zweite Nullstelle lautet $x_2=-4$.

Öffne das Arbeitsblatt: https://mathe.zone/data/arbeitsblaetter/quadratische-funktionen.pdf Löse die Aufgabe 6 k und vergleiche deine Ergebnisse mit den Lösungen.

---

zur Lektionenübersicht · zur Kursübersicht · Fehler melden