keine vorherige Lektion vorhanden | Polynomform

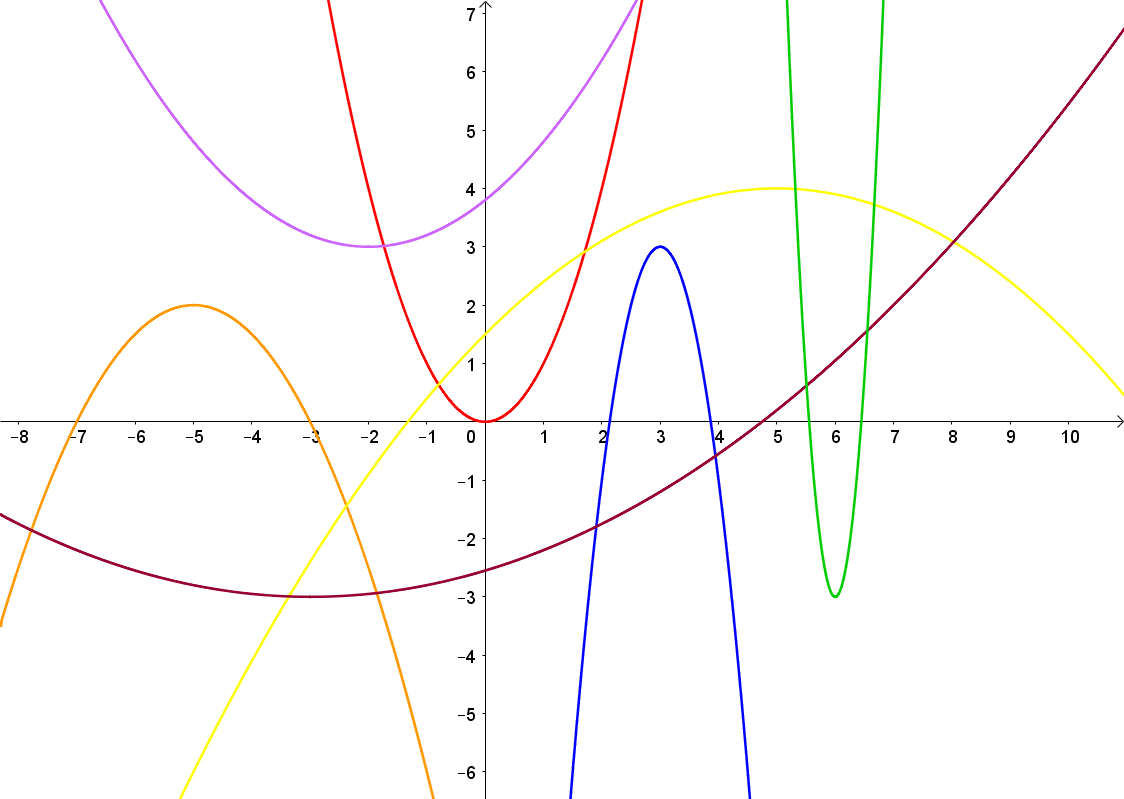
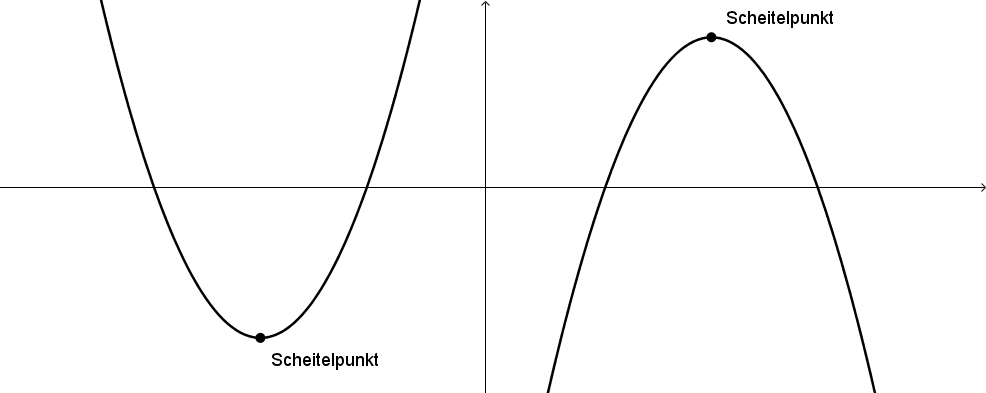
Der Graph einer quadratischen Funktion wird Parabel (exakt: quadratische Parabel) genannt. Die folgende Abbildung gibt einen Überblick, wie Parabeln aussehen. Als Scheitelpunkt bezeichnet man den höchsten bzw. tiefsten Punkt einer Parabel. Jede quadratische Funktion besitzt genau einen Scheitelpunkt. Die folgende Abbildung zeigt die beiden verschiedenen Arten von Scheitelpunkten.

Löse die folgenden Aufgaben: 17@quadratische-funktionen, 13@quadratische-funktionen

Eine quadratische Funktion ist eine Polynomfunktion, deren höchste Potenz $x^2$ ist. Im Gegensatz zur linearen Funktion, deren Funktionsgleichung normalerweise immer die Form $f(x)=k \cdot x+d$ hat, werden für das Arbeiten mit quadratischen Funktionen verschiedene Darstellungsformen der Funktionsgleichung benötigt:

• Polynomform: $f(x)=a\cdot x^2+b\cdot x+c$
• Scheitelpunktform: $f(x)=a\cdot (x-x_S)^2+y_S$
• Nullstellenform: $f(x)=a\cdot (x-x_1)\cdot (x-x_2)$

Es hängt von der Aufgabenstellung ab, welche Darstellungsform verwendet werden sollte. Quadratische Funktionen kommen u. a. in folgenden Bereichen zum Einsatz:

• Physik: Flugkurven sind unter Vernachlässigung des Luftwiderstands parabelförmig. Außerdem kann der zurückgelegte Weg bei gleichmäßiger Beschleunigung ebenfalls durch eine quadratische Funktion beschrieben werden.
• Architektur: Zahlreiche Gebäude und Strukturen sind zumindest näherungsweise parabelförmig (z. B. Brückenbögen, Hängebrücken, Hallendächer und Eingangstore).
• Wirtschaft: Beispielsweise werden quadratische Funktionen häufig verwendet, um den Gewinn oder die Kosten eines Produktionsprozesses zu beschreiben.

---

zur Lektionenübersicht · zur Kursübersicht · Fehler melden