Kurse
Logarithmusgleichungen |
keine weitere Lektion vorhanden
Bei der logarithmischen Skalierung wird bei mindestens einer Achse eines Koordinatensystems die Größe nicht linear aufgetragen sondern deren Logarithmus verwendet (meistens der dekadische Logarithmus). Dies hat den Vorteil, dass bei Größen, die über mehrere Zehnerpotenzen hinweg verteilt sind, ein besserer Überblick gewährt werden kann.
Dieser Datensatz wird nachfolgend durch ein Diagramm mit linearer Achsenskalierung dargestellt. Auf der waagrechten Achse wird die Körpergröße und auf der senkrechten Achse die Masse aufgetragen.
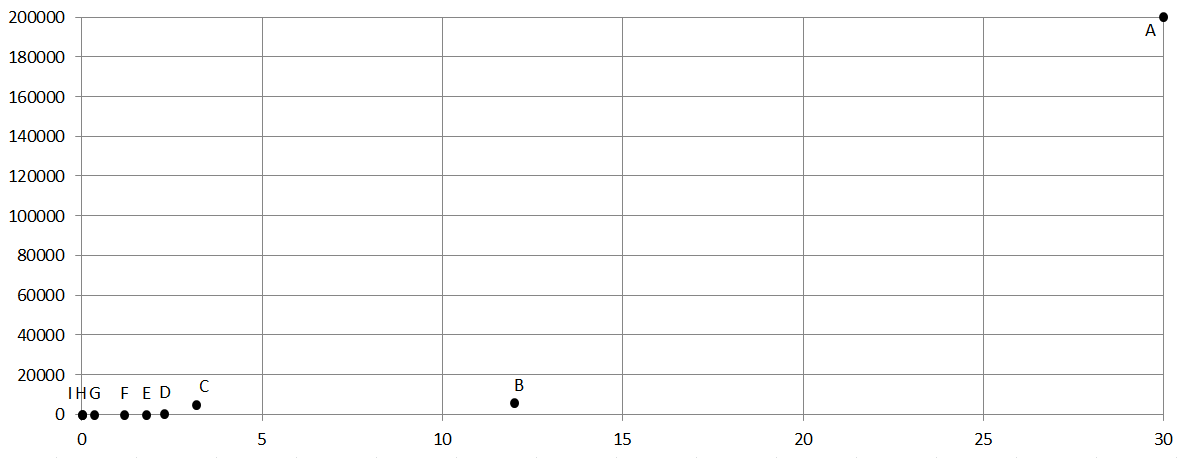
In diesem Diagramm ist es unmöglich, die Masse der meisten Tiere abzulesen. Auch die Körpergröße des Laubfrosches und der Wespe sind nicht ablesbar. Verwendet man hingegen ein Diagramm mit doppeltlogarithmischer Skalierung (d. h. beide Achsen sind logarithmisch skaliert), so können alle Werte gut abgelesen werden:

Um den Bereich zwischen den Zehnerpotenzen besser ablesen zu können, werden häufig Hilfslinien eingezeichnet (so wie im obigen Diagramm entland der x-Achse). Der Punkt H liegt beginnend bei 0,01 auf der 4. vertikalen Linie. Daher hat er den $x$-Wert 0,04 m. Der Punkt G liegt beginnend bei 0,1 zwischen der 3. und der 4. vertikalen Linie, weshalb der $x$-Wert dieses Punktes zwischen 0,3 m und 0,4 m liegt.
1. Veranschaulichung anhand eines Beispiels
In der folgenden Tabelle sind jeweils die Körpergröße (in Metern) und die Masse (in Kilogramm) verschiedener Tiere angegeben.
| Tier | Körpergröße | Masse | Punkt |
|---|---|---|---|
| Blauwal | 30 | 200000 | A |
| Tyrannosaurus | 12 | 6000 | B |
| Afrikanischer Elefant | 3,5 | 5000 | C |
| Eisbär | 2,3 | 450 | D |
| Mensch | 1,8 | 70 | E |
| Kaiserpinguin | 1,2 | 30 | F |
| Turmfalke | 0,35 | 0,2 | G |
| Laubfrosch | 0,04 | 0,005 | H |
| Wespe | 0,013 | 0,00007 | I |


Aufgabe 1
Löse die folgende Aufgabe: #190
2. Verteilung der Hilfslinien
Beim Ablesen der Werte muss beachtet werden, dass der Bereich zwischen zwei Zehnerpotenzen nicht linear verläuft. Um den Grund dafür zu verstehen, sind die folgenden Berechnungen hilfreich:
| $\lg(1)=0{,}000$ | $\lg(10)=1{,}000$ |
| $\lg(2)\approx 0{,}301$ | $\lg(20)\approx 1{,}301$ |
| $\lg(3)\approx 0{,}477$ | $\lg(30)\approx 1{,}477$ |
| $\lg(4)\approx 0{,}602$ | $\lg(40)\approx 1{,}602$ |
| $\lg(5)\approx 0{,}699$ | $\lg(50)\approx 1{,}699$ |
| $\lg(6)\approx 0{,}778$ | $\lg(60)\approx 1{,}778$ |
| $\lg(7)\approx 0{,}845$ | $\lg(70)\approx 1{,}845$ |
| $\lg(8)\approx 0{,}903$ | $\lg(80)\approx 1{,}903$ |
| $\lg(9)\approx 0{,}954$ | $\lg(90)\approx 1{,}954$ |
3. Arten von logarithmischen Diagrammen
Es gibt folgende Arten von logarithmischen Diagrammen:
- Doppeltlogarithmisch: Beide Achsen sind logarithmisch skaliert.
- Abszissenlogarithmisch: Die waagrechte Achse ist logarithmisch skaliert und die senkrechte Achse ist linear skaliert.
- Ordinatenlogarithmisch: Die senkrechte Achse ist logarithmisch skaliert und die waagrechte Achse ist linear skaliert.
© 2016 – 2024 MATHE.ZONE