Kurse

Grundlagen
Eine lineare Funktion wird verwendet, um Sachverhalte zu beschreiben, welche sich in gleichen Abständen um jeweils denselben absoluten Wert ändern. Nachfolgend ein paar Beispiele:
  • Fährt ein Auto konstant mit einer Geschwindigkeit von 80 km/h, so vergrößert sich der zurückgelegte Weg pro Stunde um 80 km.
  • Ein bestimmter Rohstoff kostet 530 € pro Tonne. Möchte ein Unternehmen um 100 kg mehr kaufen, so steigen die Kosten dadurch um 53 €.
  • Die Downloadgeschwindigkeit eines bestimmten Computerspiels beträgt konstant 2,5 MB/s. Innerhalb einer Minute verringert sich die ausstehende Datenmenge somit um 1,5 GB.
1.1.  Funktionsgleichung und Funktionsgraph
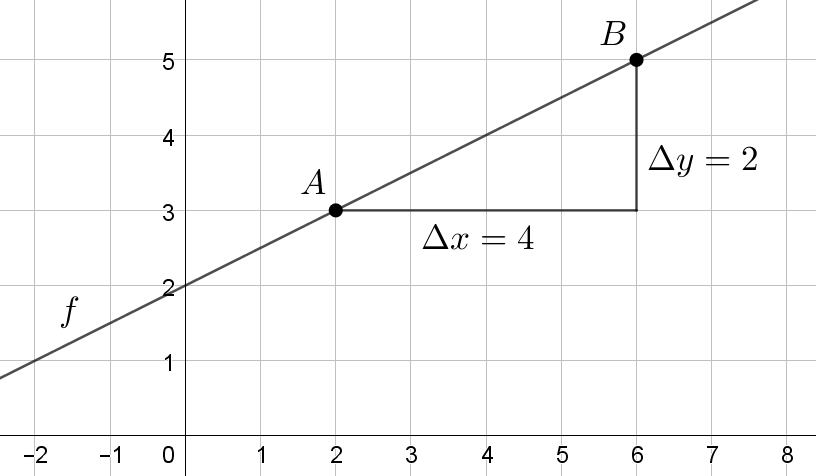
Die Funktionsgleichung einer linearen Funktion hat folgende Struktur: $$f(x)=k\cdot x+d$$ Den Parameter $k$ bezeichnet man als Steigung und den Parameter $d$ als Ordinatenabschnitt. Der Funktionsgraph einer linearen Funktion entspricht einer Gerade.

Anhand der obigen Abbildung werden nachfolgend die Parameter $k$ und $d$ erklärt.
1.2.  Ordinatenabschnitt
Als Ordinate bezeichnet man die vertikale Achse eines kartesischen Koordinatensystems. Der Ordinatenabschnitt wird daher auch häufig $y$-Achsenabschnitt genannt. Je nach Sachverhalt sind auch die Bezeichnungen Startwert bzw. Anfangswert gebräuchlich. Man verwendet für den Ordinatenabschnitt oft das Symbol $d$. Generell gilt Folgendes:
  • Ist $d>0$, so wird die $y$-Achse oberhalb der $x$-Achse geschnitten.
  • Ist $d=0$, so verläuft der Funktionsgraph durch den Koordinatenursprung.
  • Ist $d<0$, so wird die $y$-Achse unterhalb der $x$-Achse geschnitten.
Der Ordinatenabschnitt $d$ gibt also an, in welcher Höhe der Funktionsgraph die vertikale Achse schneidet. Er entspricht dem Funktionswert an der Stelle 0 und kann daher durch $f(0)$ berechnet werden. In der obigen Abbildung beträgt der Ordinatenabschnitt 2.
Aufgabe 1
Welchen Ordinatenabschnitt hat die Funktion mit der Gleichung $f(x)=3x$?
Lösung: 0, denn statt $f(x)=3x$ könnte man auch $f(x)=3x+0$ schreiben
1.3.  Steigung
Die Steigung $k$ ist ein Maß dafür, wie steil die Gerade ansteigt bzw. abfällt. Konkret gibt sie an, wie sich der Funktionswert ändert, wenn die unabhängige Variable $x$ um 1 vergrößert wird. Man unterscheidet drei Fälle:
  • Ist $k>0$, so ist die Gerade nach rechts ansteigend (streng monoton steigend).
  • Ist $k=0$, so ist die Gerade waagrecht (parallel zur $x$-Achse). Man spricht in diesem Fall von einer konstanten Funktion (weil sie überall denselben Wert hat).
  • Ist $k<0$, so ist die Gerade nach rechts abfallend (streng monoton fallend).
Aufgabe 2
a) Welche Steigung hat die Funktion mit der Gleichung $f(x)=x+3$?
b) Welche Steigung hat die Funktion mit der Gleichung $f(x)=-x+3$?
Lösung: a) 1, denn statt $x$ könnte man auch $1\cdot x$ schreiben
b) $-1$, denn statt $-x$ könnte man auch $-1\cdot x$ schreiben
Kennt man zwei beliebige Punkte $A(x_A\,|\,y_A)$ und $B(x_B\,|\,y_B)$ des Funktionsgraphen, so kann die Steigung durch die folgenden Formeln bestimmt werden: $$k=\frac{\Delta y}{\Delta x}=\frac{y_A-y_B}{x_A-x_B}=\frac{y_B-y_A}{x_B-x_A}$$ Verwendet man diese Formel für die obige Abbildung, so erhält man folgende Steigung: $$k=\frac{2}{4}=\frac{1}{2}$$ Das Symbol $\Delta$ ist der griechische Großbuchstabe Delta. Damit werden in der Mathematik und in den Naturwissenschaften häufig Abstände bezeichnet. Hier ist $\Delta y$ der vertikale Abstand zwischen zwei Punkten und $\Delta x$ der horizontale Abstand zwischen zwei Punkten.
Graphisch kann man die Steigung über das sogenannte Steigungsdreieck bestimmen. Dazu wählt man zwei möglichst weit entfernte Punkte der Gerade und zeichnet durch einen Punkt eine waagrechte Linie und durch den anderen eine senkrechte Linie. Nun misst man den Vertikalabstand $\Delta y$ und den Horizontalabstand $\Delta x$ und bildet den Quotienten (siehe obige Formel). Das Vorzeichen der Steigung ergibt sich, indem man überprüft ob die Gerade steigend (positives Vorzeichen) oder fallend (negatives Vorzeichen) ist.
1.4.  Einsatzgebiete
Lineare Funktionen kommen u. a. in folgenden Situationen zum Einsatz:
  • Physik: Beispiele für lineare Funktionen in der Physik sind die Wegfunktion $s(t)=s_0+v\cdot t$ der gleichförmigen Bewegung, die Geschwindigkeitsfunktion $v(t)=v_0+a\cdot t$ der gleichmäßig beschleunigten Bewegung oder das Ohmsche Gesetz $U(I)=R\cdot I$.
  • In der Wirtschaft kommen lineare Funktionen in Form von Kosten- und Tariffunktionen vor, da diese häufig aus einem konstanten Anteil (Fixkosten, Grundgebühr) und einem linearen Anteil bestehen. Ein Beispiel für einen Stromtarif wäre $K(x)=3{,}50+0{,}07x$. Hier beträgt die Grundgebühr 3,50 € und pro Kilowattstunde werden zusätzlich 7 c verrechnet.
  • Des Weiteren können viele Wachstums- und Abnahmeprozesse näherungsweise durch eine lineare Funktion beschrieben werden. Beispiele dafür sind das Bevölkerungswachstum bestimmter Länder, das Wachstum von Tropfsteinen, der Wasserstand eines Schwimmbeckens beim Füllen bzw. Leeren oder das Abbrennen einer Kerze.
Feedback
Wie hilfreich war dieses Kapitel für dich?
© 2016 – 2026   MATHE.ZONE