Funktionsgraph zeichnen
In diesem Kapitel wird erklärt, wie man den Funktionsgraph zeichnet, wenn man die Funktionsgleichung kennt. Der Funktionsgraph entspricht einer Gerade. Daher benötigt man genau zwei Punkte, um den Graphen zeichnen zu können. Nachfolgend werden einige Methoden dafür vorgestellt.
Ganzzahlige Steigung
- Es wird beim Ordinatenabschnitt ein Punkt gezeichnet.
- Von diesem Punkt geht man 1 nach rechts.
- Nun geht man so weit nach oben/unten, bis man den Wert der Steigung erreicht hat (bei k=2 geht man 2 nach oben, bei k=−5 geht man 5 nach unten).
- Abschließend wird eine Gerade durch Anfangspunkt und Endpunkt gezeichnet (nicht bei den Punkten aufhören, sondern darüber hinaus zeichnen).
Beispiel 1
Es soll der Graph zur Funktionsgleichung f(x)=3x−5 gezeichnet werden.
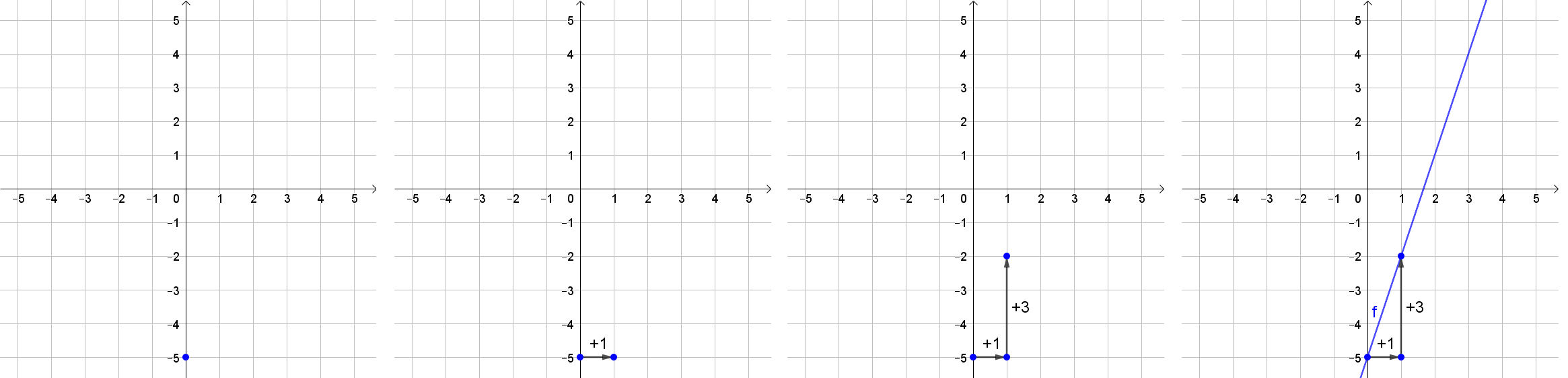

Beispiel 2
Es soll der Graph zur Funktionsgleichung f(x)=4−2x gezeichnet werden.
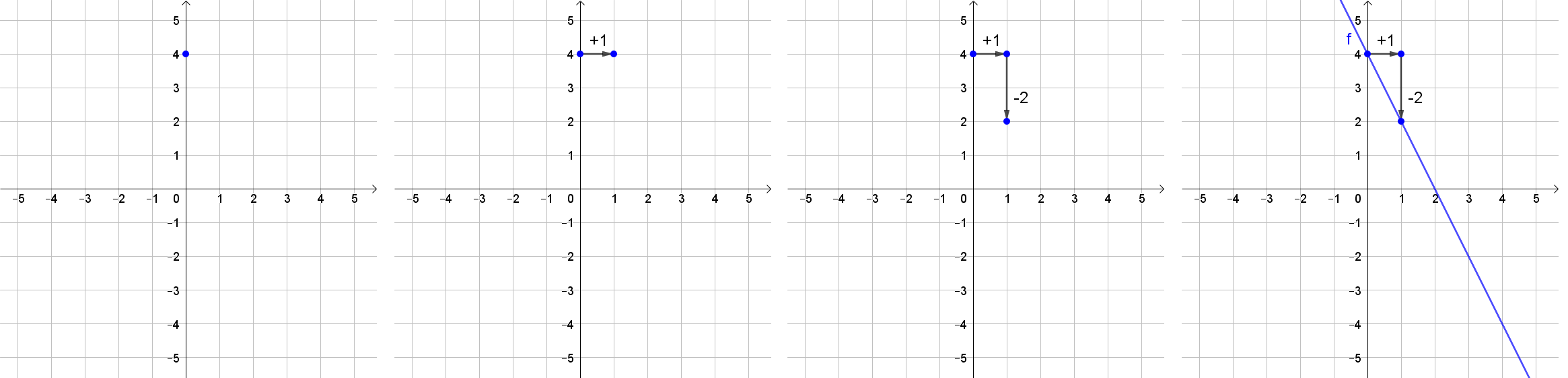

Bruch als Steigung
- Es wird beim Ordinatenabschnitt ein Punkt gezeichnet.
- Von diesem Punkt aus geht man den Nenner der Steigung (Δx) nach rechts.
- Nun geht man den Zähler der Steigung (Δy) nach oben bzw. unten (je nach Vorzeichen der Steigung).
- Abschließend wird eine Gerade durch Anfangspunkt und Endpunkt gezeichnet (nicht bei den Punkten aufhören, sondern darüber hinaus zeichnen).
Beispiel 3
Es soll der Graph zur Funktionsgleichung f(x)=32⋅x−1 gezeichnet werden.
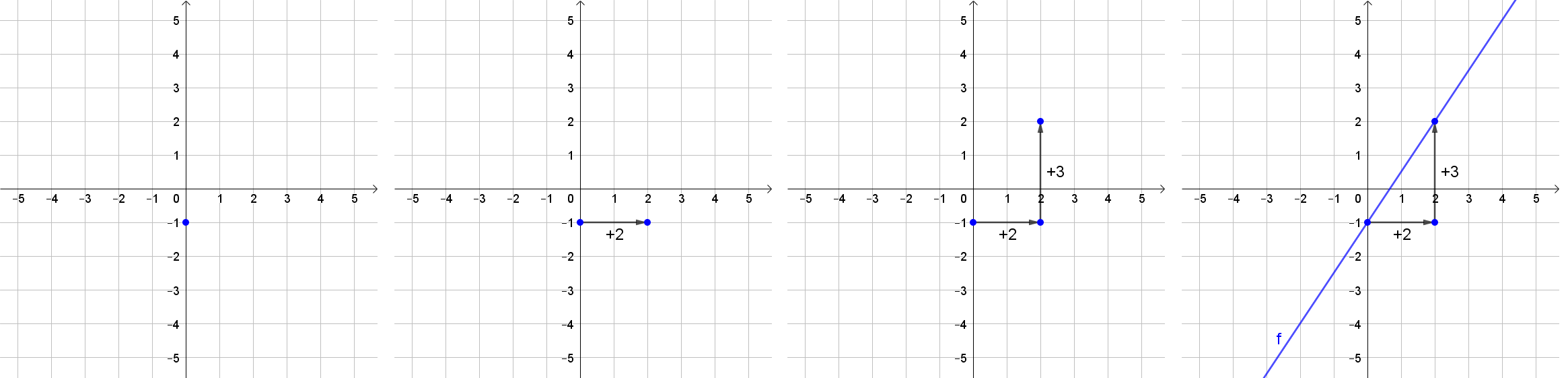

Beispiel 4
Es soll der Graph zur Funktionsgleichung f(x)=2−x4 gezeichnet werden. Hier ist die Steigung 14, denn man kann die Funktionsgleichung auch schreiben als f(x)=2−14⋅x.


Aufgabe 1
Zeichne die Funktionsgraphen in ein Koordinatensystem:
- f(x)=32x−3
- g(x)=−12x+2
- h(x)=3x
Zwei Punkte
Diese Möglichkeit funktioniert immer, ist jedoch für die oben demonstrierten „angenehmen“ Funktionsgleichungen nicht praktisch, da sie etwas länger dauert. Sie ist jedoch dann nützlich, wenn k oder d aus irgendeinem Grund unpraktisch erscheint (z. B. sehr kleine oder große Zahlenwerte oder Dezimalzahlen mit Nachkommastellen).
- Man wählt zwei x-Werte aus, die möglichst weit voneinander entfernt sind (damit sich Ungenauigkeiten beim Zeichnen nicht so stark auf das Ergebnis auswirken).
- Diese x-Werte setzt man in die Funktionsgleichung ein, um die zugehörigen y-Werte zu erhalten.
- Nun zeichnet man die beiden Punkte ins Koordinatensystem.
- Abschließend wird eine Gerade durch die beiden Punkte gezeichnet (nicht bei den Punkten aufhören, sondern darüber hinaus zeichnen).
Beispiel 5
Es soll der Graph zur Funktionsgleichung f(x)=−1,385x+26,537 gezeichnet werden.
Als x-Werte werden hier die Werte −10 und 15 ausgewählt. Die zugehörigen y-Werte erhält man durch Einsetzen in die Funktionsgleichung:
f(−10)=−1,385⋅(−10)+26,537=40,387
f(15)=−1,385⋅15+26,537=5,762
Daher verläuft die Gerade durch die Punkte (−10∣40,387) und (15∣5,762). Diese Punkte zeichnet man nun in das Koordinatensystem und legt eine Gerade durch sie.
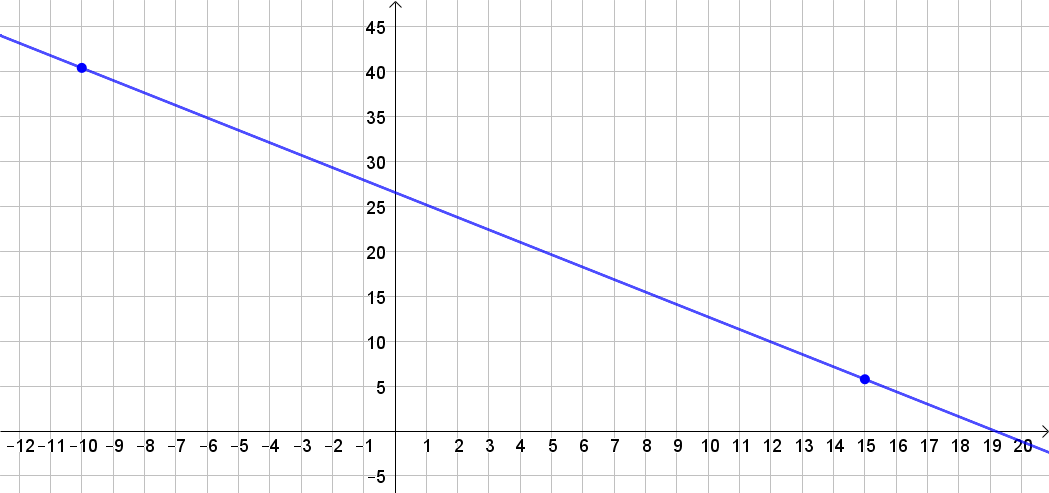

Feedback
Wie hilfreich war dieses Kapitel für dich?
© 2016 – 2025 MATHE.ZONE