Radioaktivität | keine weitere Lektion vorhanden

Exponentielle Abnahmefunktionen nähern sich von oben immer weiter dem Wert 0 an, erreichen diesen aber nie. Dieses Konzept möchte man beim beschränkten Wachstum verallgemeinern: Der Funktionswert soll sich einer bestimmten Schranke von oben bzw. von unten immer weiter annähern. Die Funktionsgleichung, mit welcher das beschränkte Wachstum bzw. die beschränkte Abnahme modelliert wird, hat folgende Gestalt: $$f(t)=S\pm c\cdot a^t \hspace{1cm}\mathrm{bzw.}\hspace{1cm} f(t)=S\pm c\cdot e^{k\cdot t}$$ Hier ist $S$ die Schranke, an welche sich der Funktionswert immer weiter annähert und $c$ ist der Anfangsabstand (also der Abstand, den die Funktion bei $t=0$ zur Schranke hat). Aus der Basis $a$ kann man erkennen, wie schnell sich die Funktion der Schranke annähert (je kleiner $a$ ist, umso schneller). Beispielsweise bedeutet $a=0{,}2$, dass der Abstand für jeden Schritt in $x$-Richtung auf 20 % des aktuellen Abstands sinkt (wie bei der exponentiellen Abnahmefunktion). Das positive Vorzeichen wird verwendet, wenn es sich um eine beschränkte Abnahme handelt (denn hier liegt die Funktion oberhalb der Schranke). Dementsprechend wird das negative Vorzeichen bei beschränkten Wachstumsfunktionen verwendet (hier liegt die Funktion unterhalb der Schranke). 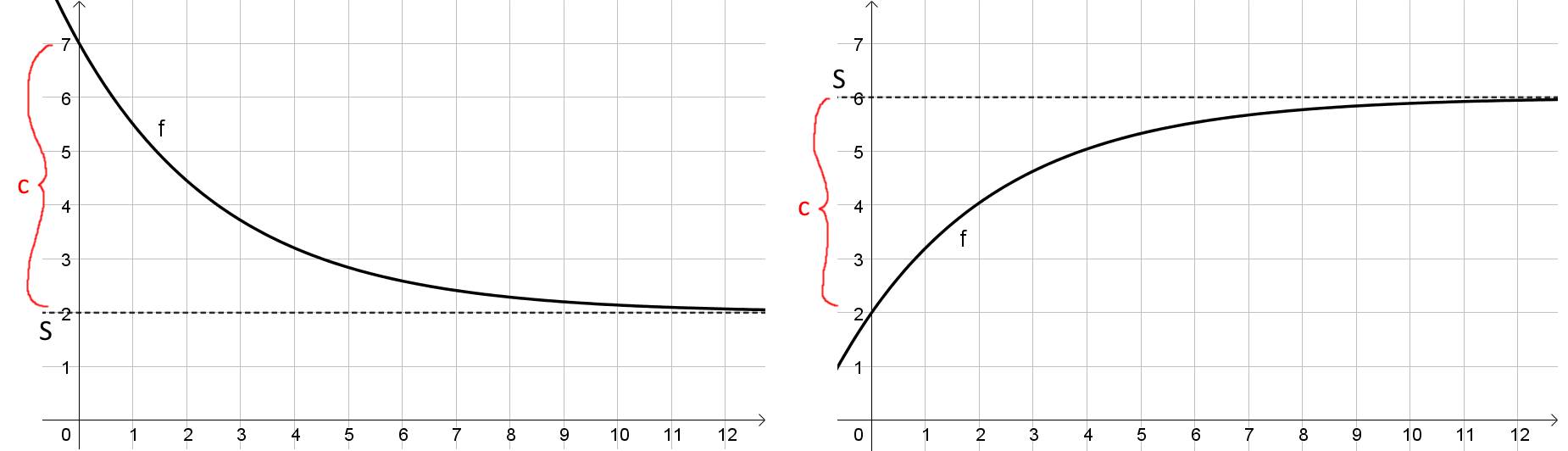Nachfolgend sind die zwei Grundformen des Funktionsgraphen dargestellt:

Es soll die Funktionsgleichung des linken Funktionsgraphen ermittelt werden. Für die Schranke erhält man den Wert $S=2$. Der Anfangsabstand beträgt $c=5$, denn der Startwert beträgt 7 und liegt somit 5 über der Schranke. Da die Funktion über der Schranke liegt (Abnahmefunktion) muss das positive Vorzeichen verwendet werden. Setzt man alle Parameter in die Grundgleichung ein, so erhält man: $$f(t)=2+5\cdot a^t$$ Für die Bestimmung von $a$ wird ein möglichst gut ablesbarer Punkt des Graphen ausgewählt. Beispielsweise eignet sich der Punkt $(2{,}5 \mid 4)$. Dessen Koordinaten werden in die obige Gleichung eingesetzt: $$4 = 2+5\cdot a^{2{,}5}$$ Durch Umformen dieser Gleichung resultiert schließlich $a\approx 0{,}6931$. Die Funktionsgleichung lautet somit $f(t)\approx 2+5\cdot 0{,}6931^t$.

Bestimme die Funktionsgleichung des rechten Graphen. Lösung: ausklappen $f(t)=6-4\cdot 0{,}7^t$ einklappen

• Temperaturanpassung eines Objektes an die Umgebungstemperatur (kaltes oder heißes Getränk, glühendes Metallstück, ...)
• Populationswachstum mit natürlicher Obergrenze
• Ladevorgang eines Akkus

Kapitelübersicht · Kursübersicht