Aufgaben zu Termen
Dieser Bereich der Website befindet sich im Umbau.
Betrachten Sie daher auch folgende Arbeitsblätter für mehr Aufgaben zu diesem Thema:
1. Terme erstellen
#446 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Ein Produkt hat den Nettopreis N. Der Verkaufspreis ist aufgrund der Mehrwertsteuer um 20 Prozent höher. Kreuze jeweils an, ob der Term geeignet ist, um den Verkaufspreis korrekt zu berechnen.
N⋅1,20
N+20
N+0,2⋅N
N⋅(1+15)
N+20100
N100⋅20
N⋅65
N⋅120100
N+15#470 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Im Haus des Meeres kostet eine Eintrittskarte für Erwachsene 16,70 €, für Kinder 7,60 € und für bestimmte Personengruppen (z. B. Senioren, Studenten, Behinderte) 12,50 €. Stelle einen Term auf, der beschreibt, wie groß die Einnahmen durch Ticketverkäufe sind, wenn e Erwachsene, k Kinder und s Personen aus den speziellen Personengruppen das Haus des Meeres besuchen!
#483 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Auf einem Parkplatz befinden sich a Autos (mit jeweils 4 Rädern) und m Motorräder (mit jeweils 2 Rädern). Erstelle einen Term, der angibt, wie viele Räder auf diesem Parkplatz sind.
Der Preis P einer Ware ändert sich. Finde jeweils einen möglichst einfachen Term, durch welchen der neue Wert der Ware beschrieben wird.
a) Der Preis P steigt um 13.3 % seines ursprünglichen Werts.
b) Der Preis P fällt auf 94.1 % seines ursprünglichen Wertes.
c) Der Preis P wird um 20 € reduziert.
d) Der Preis P sinkt um 3.7 % seines ursprünglichen Werts.
e) Der Preis P wird um 2/11 seines ursprünglichen Wertes verringert.
f) Der Preis P fällt auf 17/20 seines ursprünglichen Wertes.
#709 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Bei der „Wien läuft“-Cupwertung erhält der Sieger jedes Laufes 100 Punkte und der letzte Platz 1 Punkt. Der Punkteabstand zwischen allen Plätzen ist gleich. Beispielsweise würden bei drei Teilnehmern 100, 50.5 und 1 Punkte bzw. bei vier Teilnehmern 100, 67, 33 und 1 Punkte vergeben werden. Erstelle einen möglichst einfachen Term, der verwendet werden kann, um die Punkte des x-ten Platzes bei insgesamt n Teilnehmern zu bestimmen.
#761 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Die folgende Abbildung zeigt die ersten drei Figuren eines Musters. Finde einen Term, der für beliebige n die Anzahl der dort vorkommenden Punkte angibt.
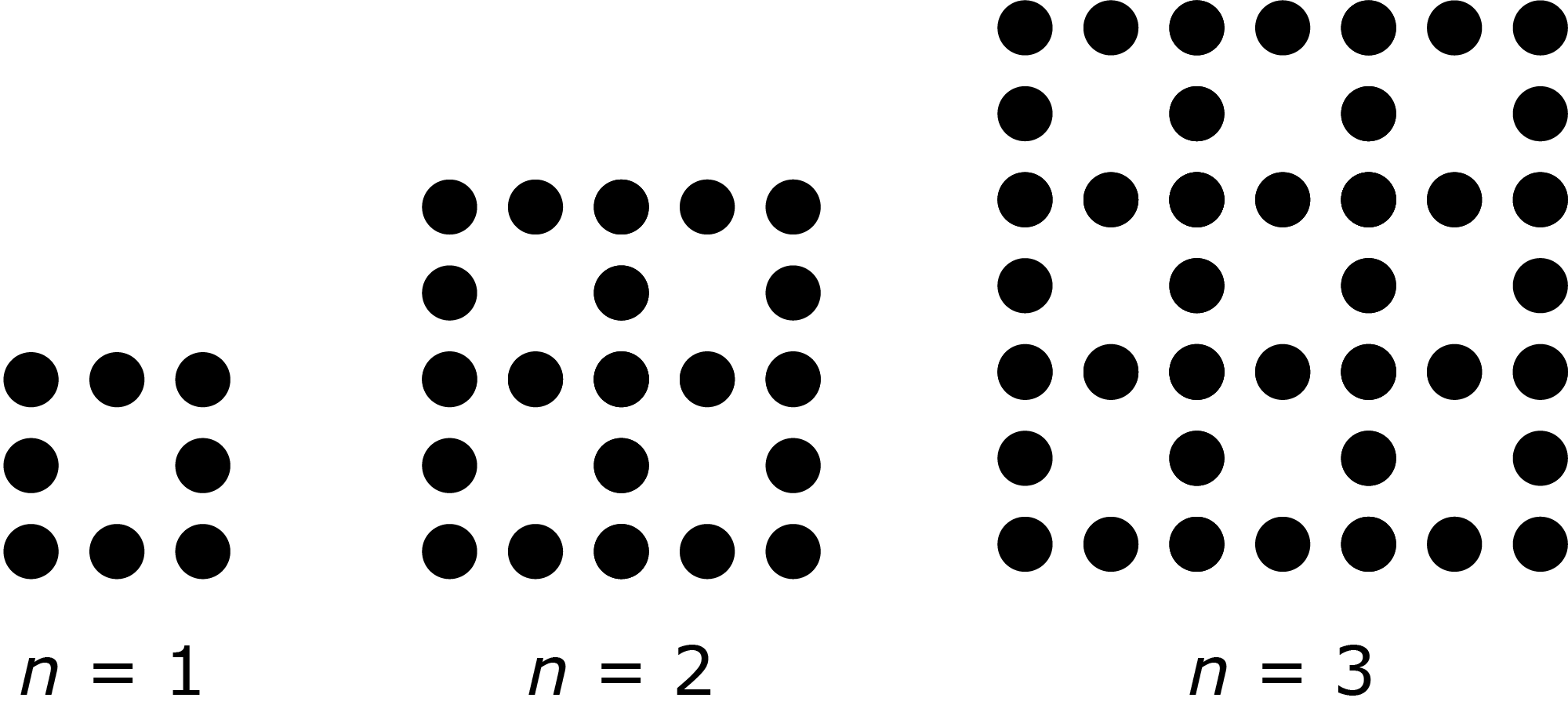
#762 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Ein Kind erstellt mit Bauklötzen ein Bauwerk nach folgendem Muster:
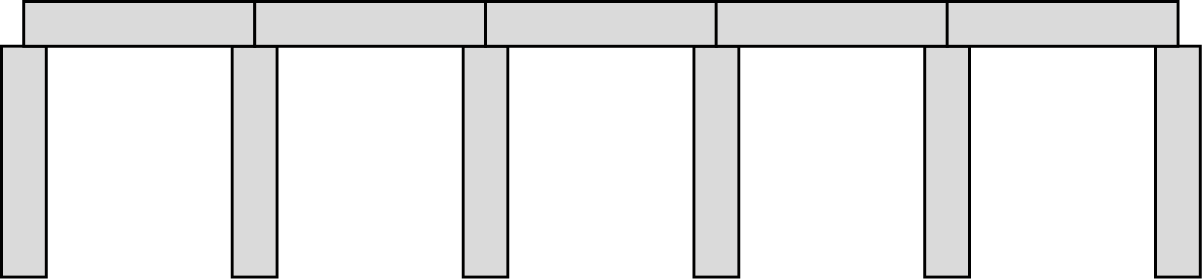
Gib einen Term an, mit dem die für die Länge n benötigte Anzahl an Bauklötzen berechnet werden kann. Mit Länge sind hier die waagrecht liegenden Klötze gemeint. Die Abbildung hätte beispielsweise die Länge 5.
#878 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Eine Schulklasse, bestehend aus n Schülern, fährt auf Wintersportwoche. Ein Fünftel der Klasse geht Langlaufen und benötigt daher keine Liftkarte. Alle anderen Schüler müssen zusätzlich zu den Grundkosten auch die Liftkarte bezahlen, welche L Euro kostet. Der Elternverein unterstützt jeden Teilnehmer mit 11 € und übernimmt zusätzlich 14 % jeder Liftkarte. Stelle einen Term auf, mit dem berechnet werden kann, wie viel der Elterverein insgesamt zahlt.
2. Rechnen mit Termen
#1068 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Ein Schüler rechnet 5⋅(x⋅y)=5x⋅5y. Erkläre, ob diese Rechnung korrekt ist und korrigiere sie gegebenenfalls.
0/1000 Zeichen
#1215 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Vereinfache die folgenden Terme so weit wie möglich.
a) 5a−(8−3b)−(−2a+9)−4b
b) 19x−(8y−(7+6x)+9y−(2+3y))) #1217 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Löse die Klammern auf und vereinfache so weit wie möglich.
a) 3⋅(2t−9)−4⋅(−15+6t)
b) 16⋅(x−9)−(−4x+3)⋅4+(5x−2)⋅(−5) #1218 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Löse die Klammern auf und vereinfache so weit wie möglich.
a) (7−6a)⋅(5b+8)
b) (6+9x)⋅(−4y+3)−(6x−9)⋅(8+7y)
c) (5s−4t+5)⋅(8s−9) 3. Potenzen
Gib an, welche Hochzahl für n eingesetzt werden muss, damit die Rechnung stimmt.
a) a5⋅a−6⋅an⋅a=a13
b) b5bn=b16
#1065 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Gib an, ob die folgenden Aussagen wahr oder falsch sind.
Es gilt allgemein (x+y)2=x2+y2.
3752−1=3742
−24=16
5⋅73=353
320 ist das Dreifache von 319.
2030 ist das Doppelte von 1030.
1050 ist das Doppelte von 1025.#1066 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Gib an, ob die folgenden Aussagen wahr oder falsch sind.
Bei der Multiplikation von Potenzen gleicher Basis werden die Hochzahlen multipliziert.
Bei der Division von Potenzen gleicher Basis werden die Hochzahlen subtrahiert.
Bei der Multiplikation von Potenzen gleicher Basis werden die Hochzahlen addiert.
Werden Potenzen potenziert, so werden die Hochzahlen multipliziert.#1220 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Vereinfache die folgenden Terme so weit wie möglich. Das Ergebnis soll keine Klammern und keine negativen Exponenten enthalten.
a) −(5a6bc3)6
b) (−4x−5y5z−6)−3
#1221 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Vereinfache den folgenden Term so weit wie möglich. Das Ergebnis soll keine Klammern und keine negativen Exponenten enthalten. Jede Variable darf nur einmal vorkommen.
(12u5v0w−518u2v−3w2)−2
#1222 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Vereinfache den folgenden Term so weit wie möglich. Das Ergebnis soll keine Klammern und keine negativen Exponenten enthalten. Jede Variable darf nur einmal vorkommen.
(6xy510x6y−4)2:15x7x−2y3⋅14x2y−5
#1252 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Vereinfache so weit wie möglich!
a) a−4⋅a0⋅a5
b) b⋅b2b−7
c) 7⋅(4c3+3c)−6c⋅(3−6c2) 4. Binomische Formeln
Vereinfache den folgenden Term so weit wie möglich und gib die Koeffizienten a,b,c an:
4⋅(3x−8)2−(17−x)⋅(6x−18)= ... =a⋅x2+b⋅x+c
Ergänze die Lücken!
(3z− _)2= _z2−150z+ _
#1235 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Berechne das Ergebnis mit Hilfe der binomischen Formeln!
a) (4a−3b)2
b) (−4+t7)2
c) (13+x8)⋅(13−x8)#1238 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Vereinfache den folgenden Term so weit wie möglich!
5⋅(8x−5y)⋅(8x+5y)−6⋅(9x−4y)2
5. Faktorisieren
Faktorisiere die folgenden Terme so weit wie möglich
a) 12ab−66b2
b) 100−x2
c) 6⋅(t−5)+s⋅(5−t)
d) 128+32z+2z2
#1245 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Hebe den vorgegebenen Term heraus: 40a2+18a−7=4a⋅(...)
6. Bruchterme
#1214 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Gib jeweils an, für welche x die Bruchterme nicht definiert sind.
a) 5x1x−4
b) 2(x+1)⋅(4−x)
c) 7x249−x2
#1246 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Vereinfache den folgenden Term so weit wie möglich. Das Ergebnis soll aus einem einzigen Bruch bestehen und keine Klammern enthalten.
x−1x+8−x+2x−7
#1247 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Erkläre, ob die folgenden Umformungen korrekt sind bzw. beschreibe andernfalls den Fehler ausführlich.
a) 3x3x+6=16
b) x−6x+5−x+8x+5=x−6−x+8x+5
7. Vermischte Aufgaben
Die Anzahl an Karten, die man für ein Kartenhaus mit n Stockwerken benötigt, kann durch folgenden Term beschrieben werden:
3n2+n2
Wieviele Karten benötigt man für ein Kartenhaus mit 4 Stockwerken?
Begründe, warum für jede natürliche Zahl gilt, dass das Quadrat dieser Zahl um 1 größer ist als das Produkt der beiden Nachbarzahlen. Beispielsweise ist 102=100 und 9⋅11=99.
#468 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Herr Maier besitzt ein quadratisches Grundstück. Um ein geplantes Projekt umsetzen zu können, möchte die Gemeinde eine Seite seines Grundstückes um 6.7 m verkürzen und als Ausgleich dafür die andere Seite um 6.7 m verlängern.
a) Begründe rechnerisch, warum Herr Maier diesem Vorhaben nicht ohne Weiteres zustimmen sollte.
b) Wie viel müsste ihm die Gemeinde als Ausgleich zusätzlich zahlen, wenn der Grundstückspreis 64 €/m² beträgt?
#471 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Im Internet findet man zahlreiche mathematische Zaubertricks, bei denen „erraten“ wird, an welche Zahl man denkt. Ein Beispiel dafür wäre folgende Anleitung:
▪
Denke an eine beliebige Zahl. ▪
Multipliziere diese mit 2. ▪
Multipliziere sie nun mit 5. ▪
Teile das Ergebnis durch deine ursprüngliche Zahl. ▪
Ziehe 7 davon ab. ▪
Die Zahl, die du nun erhältst, lautet 3.
a) Überprüfe zunächst für eine beliebige Zahl, ob dieser Trick funktioniert. Gib alle Schritte an!
b) Erkläre, warum dieser „Zaubertrick“ immer funktioniert. Verwende dazu anstelle einer beliebigen Zahl eine Variable. Schreibe abschließend eine Begründung.
#481 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Insgesamt fahren S Schüler auf Exkursion. Die Eintrittskosten betragen E Euro pro Schüler. Die Kosten für den Bus betragen für alle Schüler gemeinsam B Euro. Für Lehrer entstehen bei der Exkursion keine Kosten.
a) Gib einen Term an, der die Gesamtkosten für diese Exkursion beschreibt.
b) Berechne die Gesamtkosten für 50 Schüler, wenn die Eintrittskosten pro Schüler 3 € betragen und insgesamt Buskosten in der Höhe von 606 € entstehen.
c) Beschreibe, was mit dem Term E+BS berechnet wird.
#482 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Man wähle zwei beliebige Zahlen, für die gilt a<b. Verringert man die kleinere Zahl a um 1 und erhöht die größere Zahl b um 1, so ist das Produkt der neuen Zahlen immer kleiner als a⋅b. Beweise diese Aussage und schreibe eine nachvollziehbare Begründung!
© 2016 – 2025 MATHE.ZONE