Aufgaben zum Logarithmus
Auf dieser Seite befinden sich Aufgaben zum Logarithmus. Jede Aufgabe besitzt eine Nummer, über welche sie durch die Suchfunktion jederzeit wieder aufgerufen werden kann. Dazu muss als Suchbegriff die Aufgabennummer mit einer Raute davor eingegeben werden, also z. B. #123. Die Aufgaben dieser Internetseite werden in jeder Session – also nach jedem Neustart des Webbrowsers oder nach jedem neuen Login – neu generiert. Bei den meisten Aufgaben bedeutet dies, dass sich einzelne Zahlenwerte verändern. Möchte man zu einem späteren Zeitpunkt erneut auf exakt dieselbe Aufgabe zugreifen, so sollte daher ein Screenshot angefertigt werden.
Inhaltsverzeichnis
1. Logarithmen berechnen
#193 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Erkläre in eigenen Worten, wie man den Logarithmus $\log_{4}(493)$ ohne Taschenrechner relativ genau abschätzen kann. Es sollen zumindest die Stellen vor dem Komma stimmen.
#317 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Beschreibe, wie man ohne Taschenrechner sofort erkennen kann, dass $\lg(250)$ zwischen 2 und 3 liegt.
#1227 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Bestimme den Wert der folgenden Logarithmen auf vier Nachkommastellen genau.
$\lg(267)$
$\ln(68.3)$
$\log_{3}(0.81)$ 2. Rechenregeln für Logarithmen
#337 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Ordne jedem Term der zweiten Spalte den äquivalenten Term der dritten Spalte zu, indem du den entsprechenden Buchstaben ergänzt.
| A | $\log(c)-\log(b)-\log(a)$ | $\log\left( \frac{a+b}{c} \right)$ | |
| B | $\log(c)-\log(a+b)$ | $\log\left( \frac{c}{b+a} \right)$ | |
| C | $\log(b+a)-\log(c)$ | $\log\left( \frac{a\cdot b}{c} \right)$ | |
| D | $\log(a)+\log(b)-\log(c)$ | $\log\left( \frac{c}{a\cdot b} \right)$ | |
| E | $\log(a)-\log(b)-\log(c)$ | $\log\left( \frac{a}{c\cdot b} \right)$ |
#517 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Ordne jedem Term der zweiten Spalte den äquivalenten Term der dritten Spalte zu, indem du den entsprechenden Buchstaben ergänzt.
| A | $\log\left( \frac{x\cdot y^2}{z} \right)$ | $\log(y)+\log(z)+\log(x)-\log(2)$ | |
| B | $\log\left( \frac{z\cdot x}{2y} \right)$ | $\log(z)+\log(x)-\log(2y)$ | |
| C | $\log\left( \frac{x-2y}{z} \right)$ | $2\cdot \log(y)+\log(x)-\log(z)$ | |
| D | $\log\left( \frac{x\cdot y\cdot z}{2} \right)$ | $\log(x-2y)-\log(z)$ |
#971 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Gib an, ob die folgenden Umformungen richtig oder falsch sind.
$\log(a\cdot b^2)=\log(a)+\log(b)+\log(b)$
$\log(a^2\cdot b)=2\cdot \log(a)\cdot \log(b)$
$\log(a+b^2)=\log(a)\cdot \log(b^2)$
$\log\left(\frac{a}{b^2}\right)=\log(a)-2\cdot \log(b)$
$\log\left(\frac{a^2}{b}\right)=2\cdot \log\left(\frac{a}{b}\right)$#972 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Kreuze jeweils an, ob die folgenden Aussagen wahr oder falsch sind.
$\log(x\cdot y^2) = \log(x)+2\cdot \log(y)$
$\log(x^2\cdot y) = \log(x)+\log(x)+\log(y)$
$\log(x^2-y) = \frac{\log(x^2)}{\log(y)}$
$\log\left(\frac{x^2}{y}\right) = 2\cdot \log\left(\frac{x}{y}\right)$
$\log\left(\frac{x}{y^2}\right) = \log(x)-2\cdot \log(y)$#1228 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
a) Beschreibe durch einen vollständigen Satz, wann das Ergebnis von $\log_a(x)$ negativ ist, wenn für die Basis $a>1$ gilt.
b) Beschreibe durch einen vollständigen Satz, wann das Ergebnis von $\log_a(x)$ negativ ist, wenn für die Basis $0< a<1 $ gilt.
#1284 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Zerlege folgende Terme in eine Darstellung mit einfachsten Numeri (also möglichst kleine Terme innerhalb der Logarithmen).
a) $~\log \left( \frac{y^2}{\sqrt[7]{x}} \right) $
b) $~\log \left( \sqrt{23\cdot a^8\cdot b^7~ } \right) $
c) $~\log \left( \frac{z^2+3z}{z-8} \right) $#1285 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Stelle den folgenden Term durch einen einzigen Logarithmus dar und vereinfache so weit, wie möglich!
$$ \ln\left(a^2-b^2\right)- 2\cdot \ln(a-b) $$
3. Exponentialgleichungen
#520 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Erstelle aus der nachfolgenden Formel für den Endwert einer nachschüssigen Jahresrente eine Formel zur Berechnung der Jahre $n$.
$$E_{\mathrm{nach}}=R\cdot \frac{q^n-1}{q-1}$$
#1231 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Löse die folgende Exponentialgleichung!
$$1.7\cdot 2.25^{\,2.1x+4.1}-46=73$$
#1232 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Löse die folgende Exponentialgleichung!
$$3.2\cdot 1.86^x = 2.22^{\,x-2.4}$$
4. Logarithmische Skalierung
Es soll der Zusammenhang zwischen Einwohnerzahl und Fläche für verschiedene Länder in einem doppeltlogarithmischen Diagramm (jeweils mit Basis 10) dargestellt werden. Auf der horizontalen Achse wird die Fläche in km² und auf der vertikalen Achse die Einwohnerzahl in Mio. aufgetragen. Alle Punkte sollen beschriftet werden und neben dem Diagramm soll eine Tabelle mit allen zugehörigen Werten ersichtlich sein.
Folgende Länder sollen dargestellt werden: Vereinigte Staaten von Amerika, Japan, Kasachstan, Lettland, Liechtenstein
Lies die Koordinaten der Punkte D und W aus dem folgenden doppeltlogarithmischen Diagramm ab.
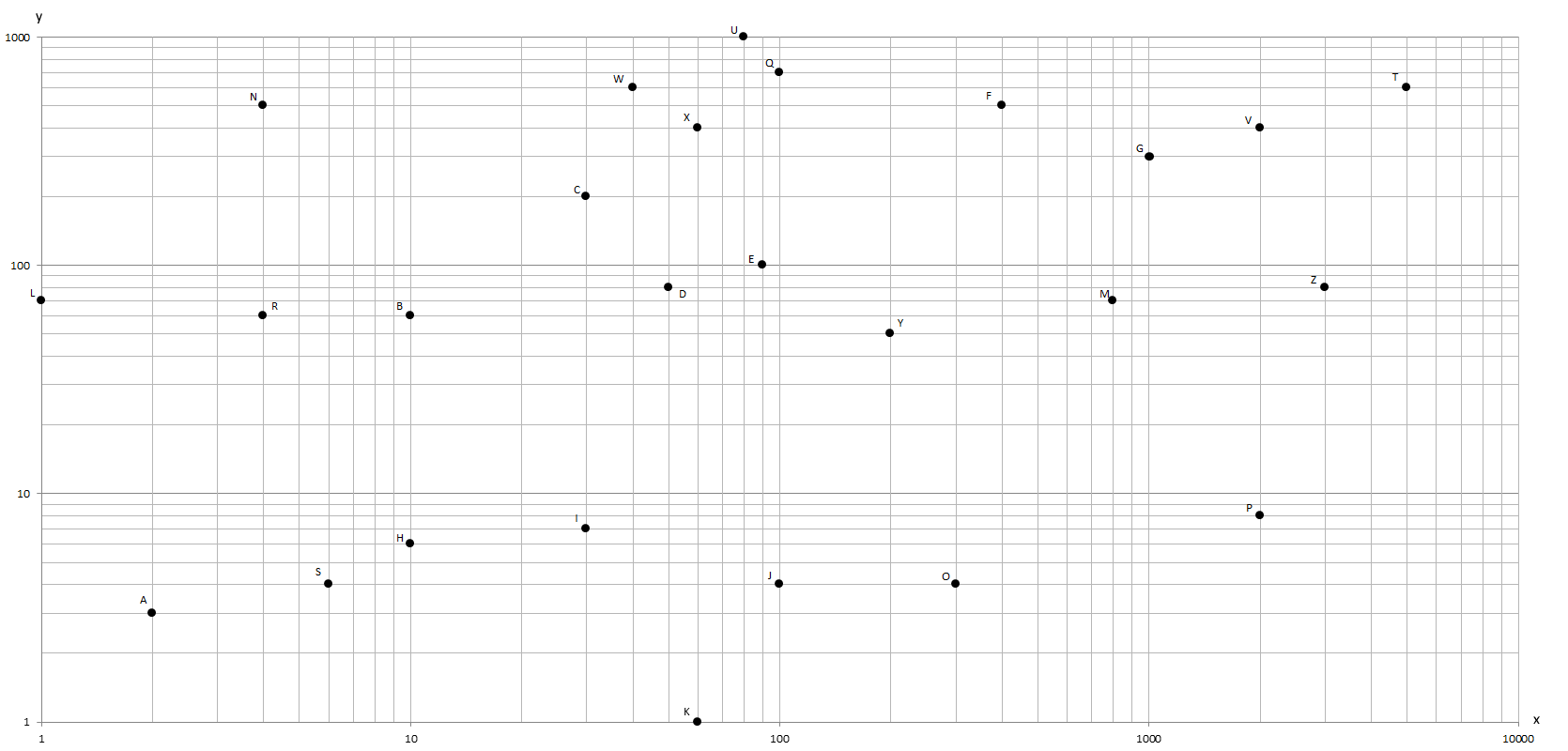
5. Vermischte Aufgaben
Ein Blatt Papier kann nur ca. sieben Mal in der Mitte gefaltet werden. Je nach Art des Papiers kann es kleine Abweichungen geben.
a) Wie oft müsste man ein 0.17 mm dickes Blatt Papier mindestens falten, damit der entstehende „Turm“ höher als 1 m ist?
b) Wie dick wäre der „Turm“, wenn das Blatt 47 Mal gefaltet wird?
c) Recherchiere im Internet nach einer vergleichbaren Größe aus der Realität, um sich das Ergebnis von Aufgabe b) besser vorstellen zu können.
Unter 405 Proben einer bestimmten Flüssigkeit befindet sich genau eine vergiftete Probe. Da die nötige chemische Analyse sehr teuer ist, werden die Proben zunächst in zwei Hälften geteilt. Von allen Proben einer Hälfte wird jeweils ein Tropfen entnommen und gemischt. Ist der Test dieser neuen Probe positiv, so weiß man, dass die vergiftete Probe in dieser Hälfte war. Andernfalls war sie in der nicht untersuchten Hälfte. Auf diese Weise lässt sich die Anzahl der in Frage kommenden Proben schrittweise halbieren. Wie viele Tests benötigt man höchstens, um die vergiftete Probe zu finden?
#1291 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Es gibt Tassen, T-Shirts und andere Artikel, auf denen man folgenden Weihnachtsgruß findet:
$$y=\frac{\log\left( \frac{x}{m}-sa \right)}{r^2} \\
yr^2 = \log\left( \frac{x}{m}-sa \right) \\
e^{yr^2} = \frac{x}{m}-sa \\
me^{yr^2} = x-msa \\
me^{rry} = x-mas$$
Erkläre, welche Umformungen zwischen den einzelnen Zeilen durchgeführt wurden.
| Urheberrechtshinweis: Die auf dieser Seite aufgelisteten Aufgaben unterliegen dem Urheberrecht (siehe Impressum). |