Aufgabe

Aufgaben werden bei jedem Laden der Seite neu generiert. Bei den meisten Aufgaben bedeutet dies, dass sich Werte in der Angabe verändern. Möchte man zu einem späteren Zeitpunkt erneut auf die selbe Aufgabe zugreifen, so sollte ein Screenshot angefertigt werden, da beim erneuten Laden der Seite neue Zahlen verwendet werden. Hinter den Eingabefeldern wird jeweils die Anzahl an Nachkommastellen angegeben. Zur Kontrolle der eigenen Rechnungen können die Lösungen eingeblendet werden.

Aufgabe 342: Die nachfolgende Grafik zeigt eine parabelförmige Bogenbrücke. An den Punkten A und C ist der Brückenbogen im Gelände verankert und Punkt B ist der Scheitelpunkt des Brückenbogens. Die Straße verläuft entlang der horizontalen Achse. Alle Angaben sind in Meter.

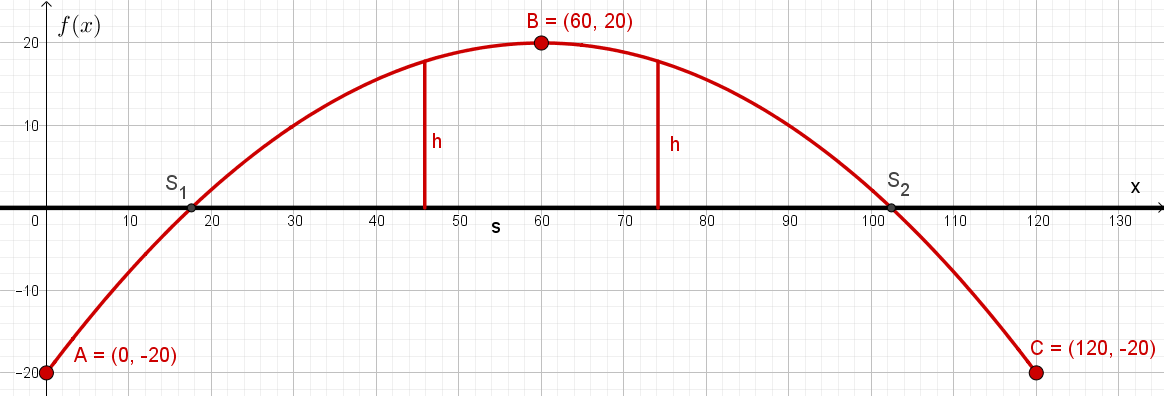
a) Ermittle eine Funktionsgleichung, welche die Form des Brückenbogens gemäß dieser Abbildung beschreibt.

Funktionsgleichung (inkl. Lösungsweg):

b) Berechne die Spannweite $s$ der Brücke, also die Entfernung zwischen den beiden Schnittpunkten S₁ und S₂ des Brückenbogens und der Straße.

Spannweite: [2] m

c) Berechne die Höhe $h$ der beiden Brückenpfeiler, welche jeweils nach einem Drittel der Spannweite errichtet werden sollen.

Höhe der Brückenpfeiler: [2] m

Lösung: keine Lösung vorhanden einklappen

Lösung: ausklappen

Urheberrechtshinweis: Diese Aufgabe unterliegt dem Urheberrecht. Nähere Informationen sind im Impressum zu finden.