Textaufgaben | keine weitere Lektion vorhanden

Bei der gleichmäßig beschleunigten Bewegung unterliegt ein Objekt einer konstanten Beschleunigung. Diese Art eines Bewegungsvorgangs kommt beispielsweise in folgenden Bereichen vor:

• Freier Fall (z. B. ein Stein, der aus einer gewissen Höhe fallen gelassen wird)
• Lotrechter Wurf (z. B. ein Ball, der senkrecht nach oben geworfen wird)
• Beschleunigungsphase eines Fortbewegungsmittels (Auto, Zug, U-Bahn, Ski, Bob, ...)
• Bremsvorgang (Auto, Zug, U-Bahn, ...)

Die Grundformel für die gleichmäßig beschleunigte Bewegung (das sogenannte Weg-Zeit-Gesetz) lautet $$s(t)=\frac{a}{2} \cdot t^2 + v_0\cdot t + s_0.$$ Dabei haben die Variablen folgende Bedeutungen:

• $t$ ... Zeit (Einheit: s)
• $s(t)$ ... Weg zum Zeitpunkt $t$ (Einheit: m)
• $a$ ... Beschleunigung (Einheit: m/s²)
• $v_0$ ... Anfangsgeschwindigkeit (Einheit: m/s)
• $s_0$ ... Weg zum Zeitpunkt 0 (Einheit: m)

Es wird ein Tennisball senkrecht nach oben geschossen. Die Bewegungsgleichung lautet $s(t)=-4{,}9t^2 +25t+12$, wobei $t$ in Sekunden und $s(t)$ in Metern gemessen wird. Der Paramter 12 bedeutet, dass sich der Ball zu Beginn 12 m über dem Bezugspunkt befindet (z. B. könnte er von einer 12 m hohen Dachterrasse nach oben geschossen worden sein). Der Parameter 25 bedeutet, dass der Ball zu Beginn die Geschwindigkeit 25 m/s hatte. Der Parameter $-4{,}9$ entspricht der halben Beschleunigung. Somit wird der Ball mit 9,8 m/s² nach unten (daher das negative Vorzeichen) beschleunigt. Dies entspricht der Gravitationsbeschleunigung auf der Erdoberfläche.

Ein Güterzug bewegt sich mit 108 km/h, als er den Bremsvorgang einleitet. Die Bremsverzögerung beträgt 0,68 m/s². Erstelle einen passenden Weg-Zeit-Zusammenhang, wobei $s(t)$ in Metern und $t$ in Sekunden gemessen wird. Der Zeitpunkt $t=0$ steht für den Beginn des Bremsvorgangs. Lösung: ausklappen $s(t)=-0{,}34t^2 +30t$ (108 km/h entspricht 30 m/s) einklappen

Die grafische Darstellung der Wegfunktion nennt man häufig Weg-Zeit-Diagramm. Dabei wird die Zeit $t$ auf der waagrechten Achse und die Strecke $s(t)$ auf der senkrechten Achse aufgetragen.

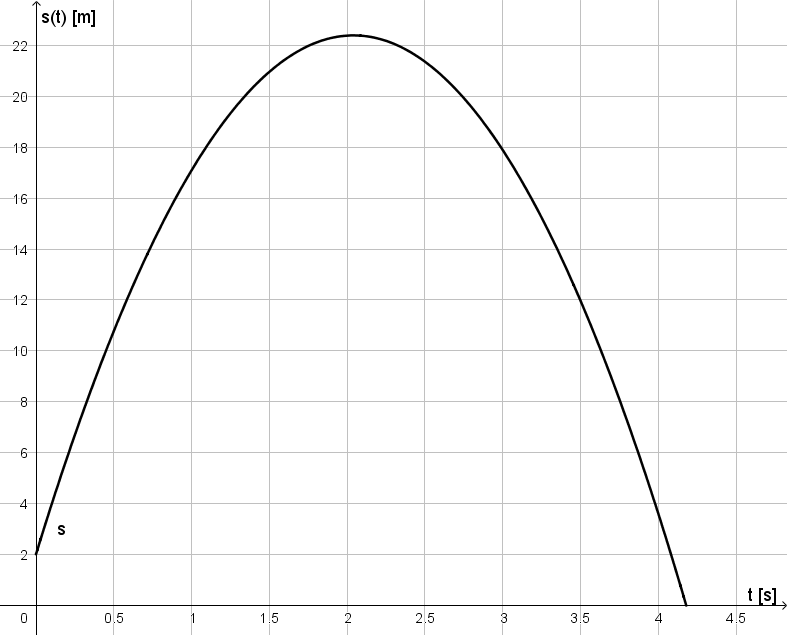
Die Höhe eines senkrecht nach oben geschossenen Balls wird durch das folgende Diagramm dargestellt. Es soll der Bewegungsvorgang möglichst präzise verbal beschrieben werden. Der Ball wird in einer Höhe von 2 m abgeschossen. Nach etwa 2 Sekunden erreicht er in ca. 22,5 m Höhe seinen höchsten Punkt. Nach ungefähr 4,2 Sekunden landet der Ball am Boden.

Während eines gleichmäßig beschleunigten Bewegungsvorgangs ändert sich die Geschwindigkeit ständig. Möchte man die mittlere (durchschnittliche) Geschwindigkeit $\bar v$ in einem bestimmten Zeitintervall berechnen, so wird dafür folgende Formel verwendet: $$\bar v = \frac{s(t_2)- s(t_1)}{t_2-t_1}$$

Ein Fahrzeug beschleunigt aus dem Stillstand gemäß der Funktion $s(t)=1{,}6t^2$, wobei $t$ in Sekunden und $s(t)$ in Metern gemessen wird. Es soll die mittlere Geschwindigkeit im Zeitintervall $[2\,\mathrm{s};~5\,\mathrm{s}]$ berechnet und in der Einheit km/h angegeben werden. Durch Anwenden der obigen Formel erhält man: $$\bar v = \frac{1{,}6\cdot 5^2 - 1{,}6\cdot 2^2}{5-2}= 11{,}2\, \mathrm{m/s}$$ Durch Multiplikation mit 3,6 wird das Ergebnis in die Einheit km/h umgerechnet. Die mittlere Geschwindigkeit im vorgegebenen Zeitintervall beträgt somit 40,32 km/h.

---

zur Lektionenübersicht · zur Kursübersicht · Fehler melden