| Fragen
Was versteht man unter dem Begriff „Zufallsexperiment“ bzw. „Zufallsversuch“? Gib ein paar Beispiele inklusive aller möglichen Versuchsausgänge!
Lösung zeigen
Ein Zufallsexperiment bzw. Zufallsversuch ist ein Sachverhalt, dessen Ausgang nicht vorhersehbar ist, da er in irgendeiner Form vom Zufall abhängig ist. Auch wenn der Begriff „Experiment“ an physikalische Experimente erinnert, handelt es sich danei häufig um sehr alltägliche Sachverhalte:
|
Zufallsexperiment | mögliche Versuchsausgänge |
|---|
|
Münzwurf | Kopf, Zahl | |
Augenzahl beim Wurf eines gewöhnlichen Würfels | 1, 2, 3, 4, 5, 6 | |
Anzahl der Würfe bis der erste Sechser gewürfelt wird | 1, 2, 3, 4, 5, ..., ∞ | |
Anzahl der Regentage im April | 0, 1, 2, 3, ..., 29, 30
|
Was versteht man unter dem Begriff „Ereignis“? Gib ein paar Beispiele und liste alle Ausgänge auf, bei denen das Ereignis eintritt!
Lösung zeigen
Ein Ereignis ist eine Aussage über das Ergebnis eines Zufallsexperiments.
-
Die Augenzahl eines Würfels ist ungerade: $A=\{1, 3, 5\}$
-
Es werden weniger als 5 Versuche benötigt, um den nächsten Sechser zu würfeln: $B=\{1, 2, 3, 4\}$
-
Es gibt höchstens 7 Regentage im April: $C=\{0, 1, 2, 3, 4, 5, 6, 7\}$
einklappen
Was versteht man unter dem Begriff „Gegenereignis“? Gib ein Beispiel und gehe auf mögliche Fehler ein!
Lösung zeigen
Das Gegenereignis $\neg A$ eines Ereignisses $A$ enthält alle möglichen Versuchsausgänge, die nicht zum Ereignis $A$ gehören.
Beispiel 1: „Es gibt höchstens 7 Regentage im April.“ Das zugehörige Gegenereignis lautet „Es gibt mindestens 8 Regentage im April“ bzw. anders formuliert „Es gibt mehr als 7 Regentage im April“. Die Menge der Ausgänge ist $\neg A = \{ 8, 9, ..., 29, 30 \}$.
Beispiel 2: „In einer Klasse mit 26 Schülern sind mehr als 23 Schüler anwesend.“ Beim Auffinden des Gegenereignisses kann es auch hilfreich sein, sich alle möglichen Ausgänge aufzuzeichnen und die bereits im Ereignis enthaltenen Ausgänge anzumalen. Alle übrig gebliebenen Ausgänge bilden dann das Gegenereignis.
Mögliche Formulierungen für das Gegenereignis sind somit „weniger als 24 Schüler sind anwesend“ oder „höchstens 23 Schüler sind anwesend“ oder „0 bis 23 Schüler sind anwesend“.
Ein häufiger Fehler ist, dass die Begriffe „alle“ und „keine“ gegensätzlich verwendet werden. Das Gegenereignis zu „alle Schüler haben die Prüfung bestanden“ ist jedoch nicht „kein Schüler hat die Prüfung bestanden“ sondern „mindestens ein Schüler hat die Prüfung nicht bestanden“. einklappen
Welche Schreibweise wird für die Wahrscheinlichkeit eines Ereignisses verwendet?
Lösung zeigen
Für die Wahrscheinlichkeit des Ereignisses $A$ verwendet man die Schreibweise $P(A)$, wobei der Buchstabe P für das englische Wort „probability“ steht. Wenn es sinnvoll erscheint, können auch verbale Formulierungen in die Klammer geschrieben werden, beispielsweise $P(\mathrm{ Augenzahl~ungerade })$. einklappen
In welchem Bereich liegen die Werte von Wahrscheinlichkeiten immer?
Lösung zeigen
Alle Wahrscheinlichkeiten haben Werte zwischen 0 und 1 (bzw. 0 % und 100 %). Sollte ein Ergebnis außerhalb dieses Bereichs liegen (also negativ oder größer als 1), so ist es mit Sicherheit falsch. einklappen
In welchem Format können Wahrscheinlichkeiten angegeben werden?
Lösung zeigen
Falls es keine speziellen Vorgaben gibt, können Wahrscheinlichkeiten auf verschiedene Weise angegeben werden:
-
Bruch: z. B. $\frac{2}{3}$ oder $\frac{4}{36}$ (zur besseren Nachvollziehbarkeit kann es sinnvoll sein, Brüche nicht zu kürzen)
-
Dezimalzahl: z. B. 0,2 oder 0,995
-
Prozent: z. B. 20 % oder 99,5 % (das Prozentsymbol muss unbedingt angegeben werden, denn 0,5 würde ansonsten 50 % bedeuten und nicht 0,5 %)
-
Promille: z. B. 3 ‰ (auch hier muss das Symbol unbedingt angegeben werden)
einklappen
Was versteht man unter dem Begriff „Gegenwahrscheinlichkeit“ und wie lautet die allgemeine Formel?
Lösung zeigen
Die Gegenwahrscheinlichkeit ist die Wahrscheinlichkeit des Gegenereignisses. Hat beispielsweise das Ereignis $A$ die Wahrscheinlichkeit 35 %, so beträgt die zugehörige Gegenwahrscheinlichkeit 65 %. Die allgemeine Formel lautet $P(\neg A)=1- P(A)$. einklappen
Was bedeutet „klassische Wahrscheinlichkeit“, wie lautet die Formel dafür und welche Voraussetzung muss erfüllt sein?
Lösung zeigen
Sind alle Versuchsausgänge eines Zufallsexperiments gleich wahrscheinlich, so wird die Anzahl aller Elemente des Ereignisses A durch die Anzahl aller insgesamt möglichen Versuchsausgänge dividiert.
$$P(A)=\frac{\mathrm{ Anzahl~von~A }}{\mathrm{Gesamtanzahl}}$$
Beispielsweise gilt diese Formel beim Münzwurf, beim Werfen eines Würfels, beim Roulette und bei vielen weiteren Glücksspielen. In sehr vielen anderen Fällen sind jedoch nicht alle Versuchsausgänge gleich wahrscheinlich (z. B. die Anzahl der Regentage im April, denn es ist besonders unwahrscheinlich, dass es tatsächlich an allen 30 Tagen regnet, während drei bis sieben Regentage deutlich wahrscheinlicher sind). einklappen
Was bedeutet „statistische Wahrscheinlichkeit“, wie lautet die Formel dafür und welche Voraussetzung muss erfüllt sein?
Lösung zeigen
Liegen zu einem Sachverhalt besonders viele Daten vor (z. B. bei Statistiken über die Bevölkerung), so wird die Anzahl aller Elemente des Ereignisses A durch die Anzahl aller insgesamt vorhandenen Elemente dividiert.
$$P(A)=\frac{\mathrm{ Anzahl~von~A }}{\mathrm{Gesamtanzahl}}$$
Beispiel: Für die Wahrscheinlichkeit, dass eine zufällig ausgewählte Person studiert hat, dividiert man die Anzahl aller Menschen mit abgeschlossenem Studium durch die Gesamtanzahl aller Menschen. einklappen
Was bedeutet ODER in der Mathematik?
Lösung zeigen
Während man im Alltag mit „oder“ häufig entweder eine Sache oder eine andere Sache meint (aber nicht beide), ist dies in der Mathematik (und vielen anderen Gebieten wie beispielsweise der Informatik) anders. Eine ODER-Verknüpfung von zwei Ereignissen ist erfüllt, sobald zumindest eines der beiden Ereignisse eintritt, also entweder „nur A“, oder „nur B“ oder „A und B“. einklappen
Welche Symbole werden für die UND- und ODER-Verknüpfung von zwei Ereignissen verwendet? Welche praktische Merkregel gibt es hierfür?
Lösung zeigen
UND-Verknüpfung: $A\cap B$
ODER-Verknüpfung: $A\cup B$
Man kann sich dies anhand des Anfangsbuchstabens merken: Das UND-Symbol ist nach unten geöffnet und das ODER-Symbol ist nach oben geöffnet. einklappen
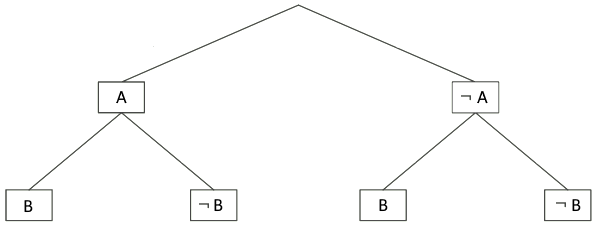
Welche Regeln gelten für Baumdiagramme?
Lösung zeigen
-
Entlang eines Pfades werden alle Wahrscheinlichkeiten multipliziert.
-
Um mehrere Pfade zusammenzufassen, werden deren Wahrscheinlichkeiten addiert.
einklappen
Was ist eine bedingte Wahrscheinlichkeit, welche Schreibweise wird dafür verwendet und wie lautet die Formel dafür?
Lösung zeigen
Mit der bedingten Wahrscheinlichkeit $P(B\mid A)$ wird berechnet, wie wahrscheinlich es ist, dass Ereignis $B$ eintritt, wenn Ereignis $A$ eingetreten ist (z. B. wie wahrscheinlich ist es, dass jemand die Prüfung besteht, wenn er fünf Tage davor zu lernen begonnen hat). Der senkrechte Strich im Ausdruck $B\mid A$ wird als „unter der Bedingung“ ausgesprochen.
Formel: $P(B\mid A)= \frac{P(A\cap B)}{P(A)}$
Beschreibung der Formel: Unter allen Möglichkeiten, bei denen $A$ eingetreten ist, werden jene ausgewählt, in denen zusätzlich auch $B$ eingetreten ist. Es wird also eine neue Grundmenge betrachtet, nämlich nur noch jene Fälle, bei denen $A$ erfüllt ist. einklappen
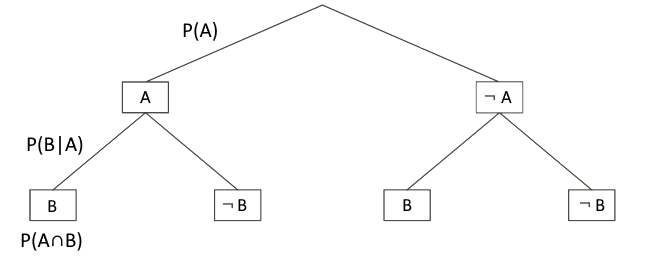
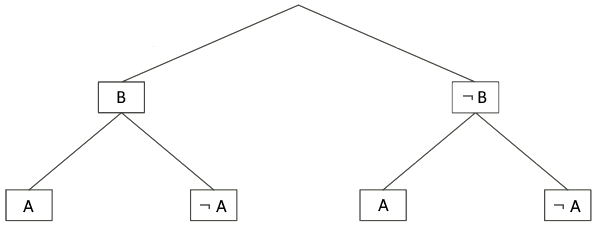
Wie kann man die Formel der bedingten Wahrscheinlichkeit anhand eines Baumdiagrammes begründen?
Lösung zeigen
Relevant für die Begründung sind nur die drei Wahrscheinlichkeiten, die im linken Pfad des folgenden Baumdiagramms eingetragen wurden:
Da die Wahrscheinlichkeiten entlang eines Pfades multipliziert werden, erhält man $P(A\cap B)= P(A)\cdot P(B\mid A)$. Dividiert man durch $P(A)$, so erhält man $P(B\mid A) = \frac{P(A\cap B)}{P(A)}$. einklappen
Wie ist eine Vierfeldertafel aufgebaut und wie hängen die einzelnen Felder zusammen? Demonstriere anhand eines Beispiels, wie man die Lücken vervollständigen kann.
Lösung zeigen
In einer Vierfeldertafel werden zwei Ereignisse miteinander verglichen. Sie enthält die Wahrscheinlichkeiten der beiden Ereignisse, deren Gegenwahrscheinlichkeiten, sowie alle UND-Verknüpfungen.
Die Summe der ersten beiden Elemente jeder Zeile bzw. Spalte entspricht dem Wert des dritten Elements. Daher wird die letzte Zeile und Spalte auch mit „Summe“ beschriftet.
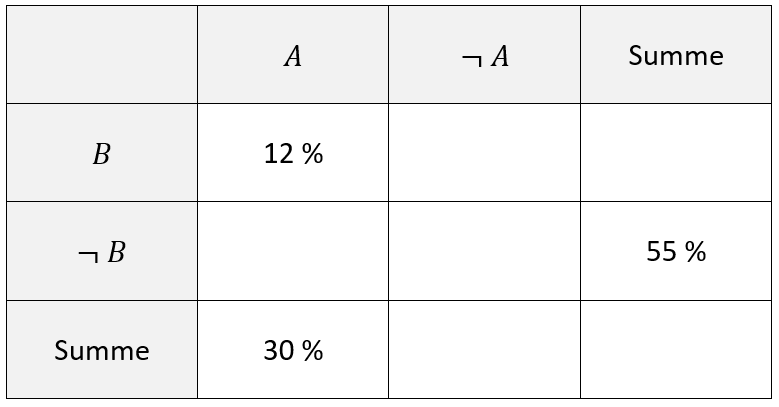
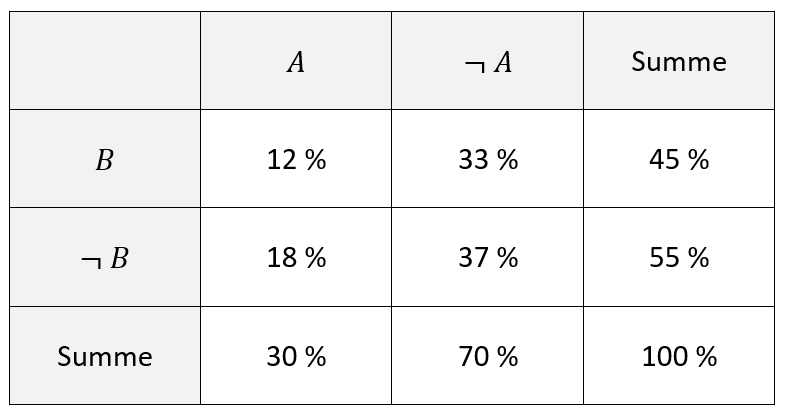
Beispiel: Es ist eine Vierfeldertafel mit folgenden Werten bekannt:
-
Es werden die beiden äußeren Werte ermittelt: $100\,\% - 30\,\% = 70\,\%$ und $100\,\% - 55\,\% = 45\,\%$
-
Die erste Zeile ergibt insgesamt 45 %, daher erhält man $45\,\% - 12\,\% = 33\,\%$.
-
Die erste Spalte ergibt insgesamt 30 %, daher erhält man $30\,\% - 12\,\% = 18\,\%$.
-
Für das letzte Element gibt es zwei Möglichkeiten: $70\,\% - 33\,\% = 37\,\%$ und $55\,\% - 18\,\% = 37\,\%$. Man sollte auch beide Rechnungen durchführen, um Fehler gegebenenfalls zu erkennen.
einklappen
Wann sind zwei Ereignisse stochastisch unabhängig?
Lösung zeigen
Die Ereignisse $A$ und $B$ sind stochastisch unabhängig, wenn die Gleichung $P(A\cap B) = P(A)\cdot P(B)$ erfüllt ist.
Begründung: Wenn $A$ und $B$ unabhängig sind, dann hat es keinen Einfluss auf $B$, ob $A$ eingetreten ist oder nicht. Das bedeutet, $P(B\mid A)= P(B)$ muss erfüllt sein. Setzt man nun auf der linken Seite die Definition der bedingten Wahrscheinlichkeit ein, also $P(B\mid A)= \frac{P(A\cap B)}{P(A)}$, so erhält man:
$$\frac{P(A\cap B)}{P(A)} = P(B)$$
Durch Multiplikation mit $P(A)$ erhält man die obige Gleichung $P(A\cap B) = P(A)\cdot P(B)$. einklappen
Welche Fälle können eintreten, wenn zwei Ereignisse nicht unabhängig sind?
Lösung zeigen
-
Falls $P(B\mid A)=P(A)\cdot P(B)$ gilt, dann sind $A$ und $B$ unabhängig.
-
Falls $P(B\mid A)>P(A)\cdot P(B)$ gilt, dann wird $B$ durch $A$ begünstigt.
-
Falls $P(B\mid A)< P(A)\cdot P(B)$ gilt, dann wird $B$ durch $A$ erschwert.
Begründung: Falls $B$ durch $A$ begünstigt wird, so gilt $P(B\mid A)> P(B)$. Setzt man links die Definition der bedingten Wahrscheinlichkeit ein, so erhält man $\frac{P(A\cap B)}{P(A)}> P(B)$. Durch Umformen folgt die obige Eigenschaft.
Falls $B$ durch $A$ erschwertwird, so gilt $P(B\mid A)< P(B)$. Setzt man links die Definition der bedingten Wahrscheinlichkeit ein, so erhält man $\frac{P(A\cap B)}{P(A)}< P(B)$. Durch Umformen folgt die obige Eigenschaft. einklappen
Wie lautet der Satz von Bayes und wofür kann er verwendet werden? Gib ein konkretes Beispiel!
Lösung zeigen
$$P(A\mid B) = \frac{P(A)\cdot P(B\mid A)}{P(B)}$$
Dieser Satz kann verwendet werden, um eine Umkehr der Bedingungen durchzuführen. Kennt man beispielsweise die Wahrscheinlichkeit, mit welcher eine kranke Person ein positives Testergebnis erhält, so kann man mit ausreichenden Zusatzinformationen berechnen, wie wahrscheinlich es ist, dass eine positiv getestete Person tatsächlich krank ist. Es wird also mittels $P(\mathrm{positiver~Test}\mid \mathrm{krank})$ die Wahrscheinlichkeit $P(\mathrm{ \mathrm{krank} \mid positiver~Test})$ berechnet. einklappen
Wie wird der Satz von Bayes richtig ausgesprochen?
Lösung zeigen
Der Satz von Bayes geht auf den englischen Mathematiker Thomas Bayes zurück, dessen Familienname bɛɪ̯z gesprochen wird. Eine Audiodatei dazu befindet sich unter folgendem Link: Audiodatei einklappen
Wie lautet die Herleitung für den Satz von Bayes?
Lösung zeigen
Ausgangspunkt sind die beiden folgenden Baumdiagramme, bei welchen jeweils die Reihenfolge der Ereignisse abwechselt.
Aus dem linken Diagramm erhält man $P(A\cap B) = P(A)\cdot P(B \mid A)$ und aus dem rechten Diagramm erhält man $P(A\cap B) = P(B)\cdot P(A \mid B)$. Durch Gleichsetzen erhält man:
$$P(A)\cdot P(B \mid A) = P(B)\cdot P(A \mid B) $$
Dies kann schließlich umgeformt werden zu:
$$P(A\mid B) = \frac{P(A)\cdot P(B\mid A)}{P(B)}$$ einklappen
Wie kann der Satz von Bayes praktisch anhand eines Baumdiagramms angewendet werden? Demonstriere anhand eines Beispiels!
Lösung zeigen
Ausgangspunkt ist folgendes Baumdiagramm, von welchem alle Wahrscheinlichkeiten bekannt sind:
Die Wahrscheinlichkeiten $P(A)$ und $P(B\mid A)$ sind bekannt sein und $P(B)$ entspricht im Baumdiagramm der Summe aller Pfade, die Ereignis $B$ enthalten, also $P(B)=P(A)\cdot P(B\mid A) + P(\neg A)\cdot P(B \mid \neg A)$. Durch Einsetzen wird der Satz von Bayes folgendermaßen erweitert:
$$P(A\mid B) = \frac{P(A)\cdot P(B\mid A)}{P(B)} = \frac{P(A)\cdot P(B\mid A)}{P(A)\cdot P(B\mid A) + P(\neg A)\cdot P(B \mid \neg A)} = \frac{\mathrm{Pfad,~der~A~und~B~enthält}}{\mathrm{alle~Pfade,~die~B~enthalten}} $$
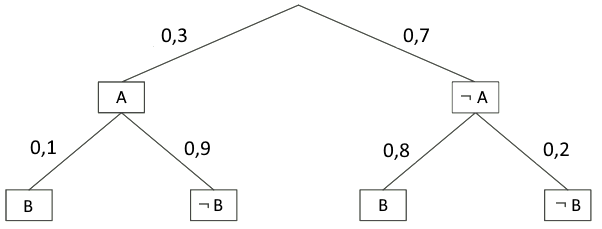
Beispiel: Es ist folgendes Baumdiagramm gegeben:
Die Wahrscheinlichkeit $P(A\mid B)$ wird folgendermaßen berechnet:
$$P(A\mid B) = \frac{0{,}3\cdot 0{,}1}{0{,}3\cdot 0{,}1 + 0{,}7\cdot 0{,}8} = 0{,}05084... \approx 5{,}08\,\%$$ einklappen
Was bedeuten die Fachbegriffe „Prävalenz“, „Sensitivität“ und „Spezifität“?
Lösung zeigen
-
Die Prävalenz beschreibt den Anteil der Bevölkerung, der an einer bestimmten Krankheit erkrankt ist.
-
Die Sensitivität ist die Wahrscheinlichkeit, mit welcher ein Test eine erkrankte Person als krank erkennt.
-
Die Spezifität ist die Wahrscheinlichkeit, mit welcher ein Test eine gesunde Person als gesund erkennt.
einklappen
Möglichkeiten zur Unterstützung
© 2016 – 2024 MATHE.ZONE
|
