Fragen zur Trigonometrie im rechtwinkligen Dreieck
Winkelfunktionen
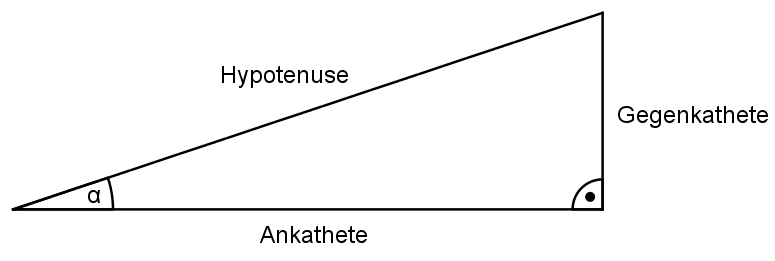
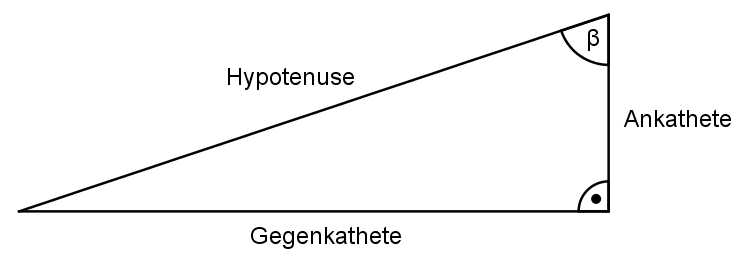
Was versteht man unter Ankathete und Gegenkathete? Beschreibe anhand passender Skizzen!
Lösung zeigen
Die Hypotenuse ist immer die längste Seite eines rechtwinkligen Dreiecks und befindet sich gegenüber des rechten Winkels. Die Position der Ankathete und der Gegenkathete sind hingegen abhängig vom betrachteten Winkel. Die Ankathete grenzt immer
an den Winkel an. Die Gegenkathete befindet sich
gegenüber des Winkels.
Wie sind die drei Winkelfunktionen definiert?
Umkehrfunktionen
Wie lauten die Umkehrfunktionen der Winkelfunktionen und welche Symbole werden dafür verwendet?
Lösung zeigen
-
Die Umkehrfunktion des Sinus heißt Arkussinus und wird mit arcsin, asin oder sin−1 bezeichnet.
-
Die Umkehrfunktion des Cosinus heißt Arkuscosinus und wird mit arccos, acos oder cos−1 bezeichnet.
-
Die Umkehrfunktion des Tangens heißt Arkustangens und wird mit arctan, atan oder tan−1 bezeichnet.
Wofür werden die Umkehrfunktionen der Winkelfunktionen verwendet?
Lösung zeigen
Die Umkehrfunktionen arcsin, arccos und arctan können verwendet werden, um mit zwei gegebenen Seitenlängen eines rechtwinkligen Dreiecks einen Winkel zu berechnen.
einklappen
Steigungswinkel und Steigung
Wie lautet der Zusammenhang zwischen Steigungswinkel und Steigung?
Lösung zeigen
Für den Steigungswinkel
α und die Steigung
k gelten die folgenden Zusammenhänge:
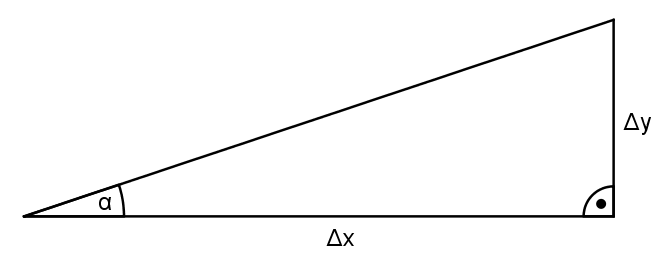
Begründung: Die Steigung entspricht dem Verhältnis
ΔyΔx. Da
Δy die Gegenkathete und
Δx die Ankathete von
α ist, entspricht dieses Verhältnis auch dem Tangens von
α. Daher gilt
k=tan(α). Die zweite Formel ergibt sich durch Anwendung der Umkehrfunktion.