Fragen zu quadratischen Funktionen
Wie lautet die Grundgleichung einer quadratischen Funktion?
Nullstellen und Schnittpunkte
Wie viele Nullstellen kann eine quadratische Funktion besitzen?
Scheitelpunkt
Was ist der Scheitelpunkt einer quadratischen Funktion? Beschreibe anhand von passenden Skizzen!
Lösung zeigen
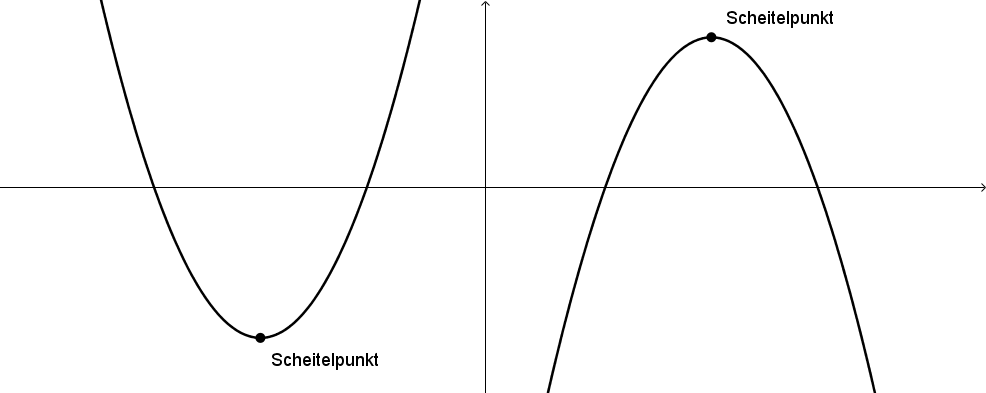
Als Scheitelpunkt bezeichnet man den höchsten bzw. tiefsten Punkt einer Parabel. Jede quadratische Funktion besitzt genau einen Scheitelpunkt. Die folgende Abbildung zeigt die beiden verschiedenen Arten von Scheitelpunkten.
Funktionsgraph
Wie nennt man den Graph einer quadratischen Funktion?
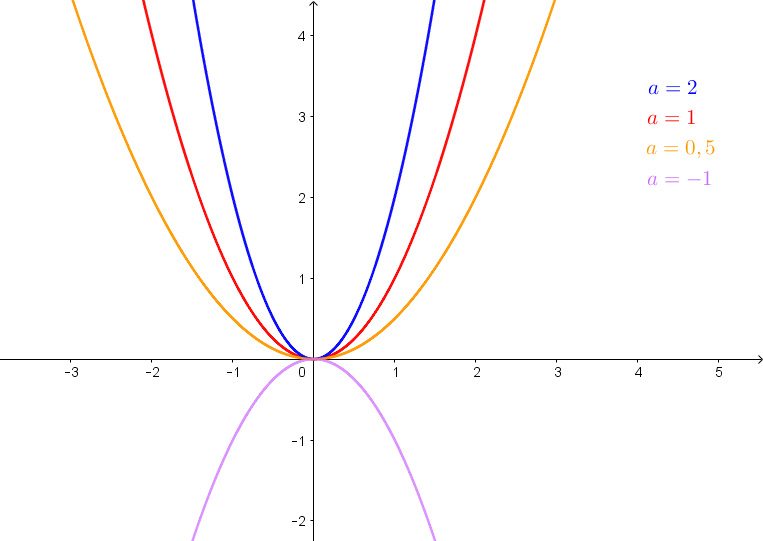
Welchen Einfluss hat der Parameter a auf den Graphen einer quadratischen Funktion mit der Gleichung f(x)=ax2+bx+c?
Lösung zeigen
Der Parameter
a beeinflusst die Krümmung der Parabel.
-
Ist a>0, so ist die Parabel nach oben geöffnet (positiv gekrümmt).
-
Ist a<0, so ist die Parabel nach unten geöffnet (negativ gekrümmt).
-
Je größer der Betrag von a ist, umso steiler/spitzer ist die Parabel.
-
Je kleiner der Betrag von a ist, umso flacher ist die Parabel.
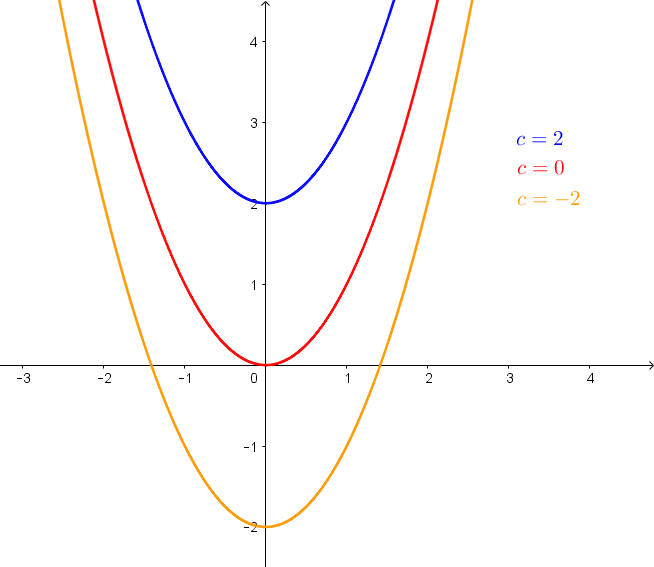
Welchen Einfluss hat der Parameter c auf den Graphen einer quadratischen Funktion mit der Gleichung f(x)=ax2+bx+c?
Lösung zeigen
Der Parameter
c entspricht dem Ordinatenabschnitt.
-
Ist c>0, so wird die y-Achse im positiven Bereich geschnitten.
-
Ist c=0, so wird die y-Achse im Koordinatenursprung geschnitten.
-
Ist c<0, so wird die y-Achse im negativen Bereich geschnitten.
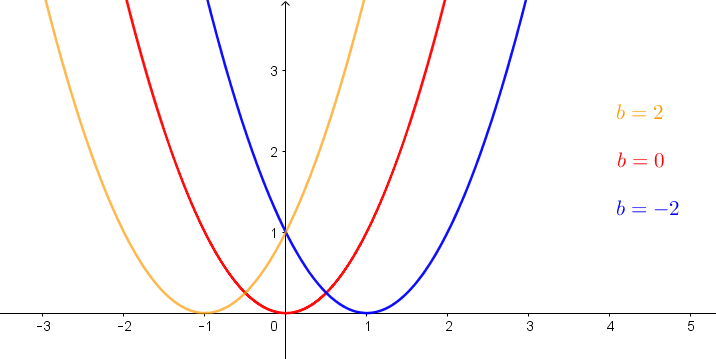
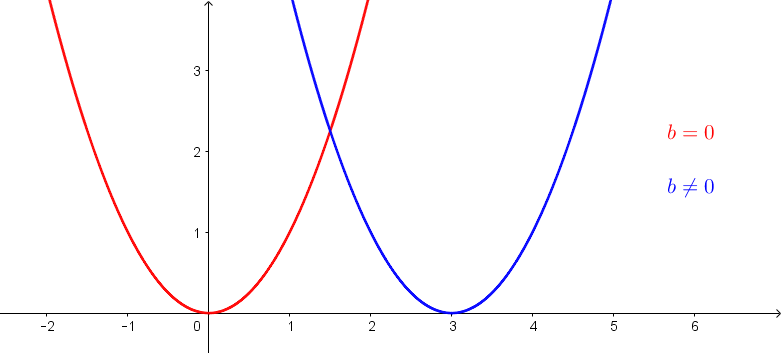
Welchen Einfluss hat der Parameter b auf den Graphen einer quadratischen Funktion mit der Gleichung f(x)=ax2+bx+c?
Lösung zeigen
Der Parameter
b entspricht der Steigung, mit welcher die Parabel die
y-Achse schneidet.
Begründung: Für diese Begründung werden Kenntnisse der Differentialrechnung vorausgesetzt. Bildet man von der Funktionsgleichung
f(x)=ax2+bx+c die Ableitungsfunktion, so erhält man
f′(x)=2ax+b. Die Ableitungsfunktion
f′ gibt an, welche Steigung die Funktion
f an der Stelle
x besitzt. Setzt man
x=0, so erhält man
f′(0)=2a⋅0+b=b. Daher wird die
y-Achse mit der Steigung
b geschnitten.
Anhand des Parameters
b kann man auch erkennen, ob die Parabel symmetrisch zur
y-Achse ist. Ist
b=0, so befindet sich der Scheitelpunkt direkt auf der
y-Achse und somit ist der Funktionsgraph symmetrisch zur
y-Achse.