Fragen zu logistischen Funktionen
Wie lautet die Funktionsgleichung einer logistischen Funktion und welche Bedeutung haben die einzelnen Parameter?
Lösung zeigen
N(t)=S1+c⋅atoderN(t)=S1+c⋅e−λ⋅t
-
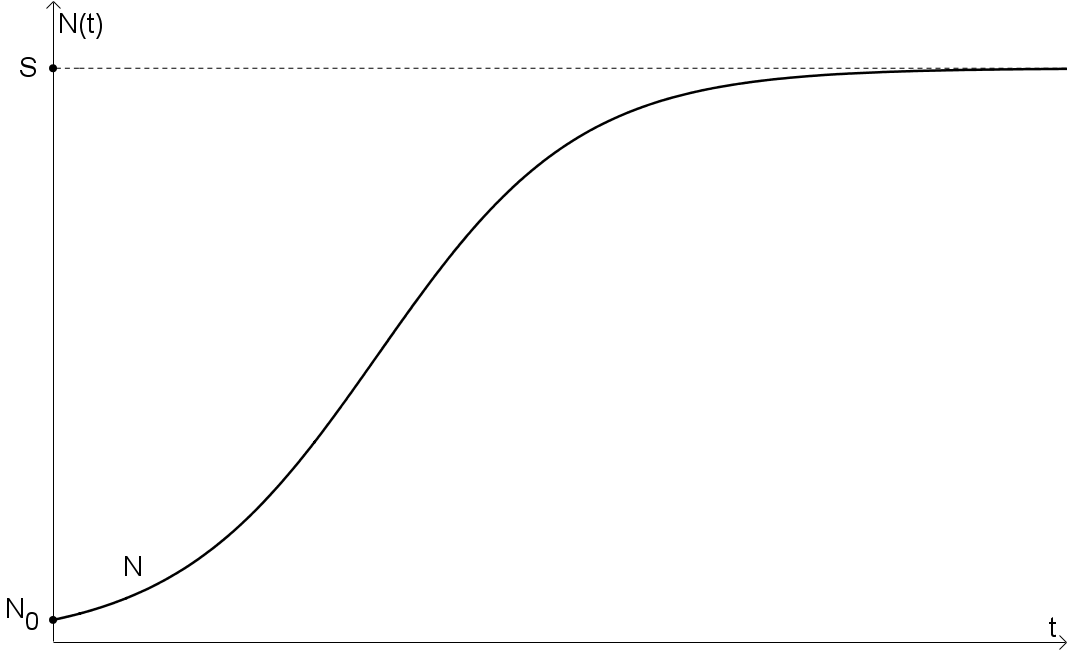
S ist die Schranke, welcher sich die Funktion für sehr große t annähert.
-
c wird berechnet durch c=S−N0N0=AnfangsabstandAnfangswert.
-
a bzw. λ beeinflusst, wie schnell sich die Funktion der Schranke annähert.
einklappen
In welchen Bereichen kommen logistische Funktionen typischerweise zum Einsatz?
Lösung zeigen
-
Verkaufszahlen: Am Beginn ist das Wachstum langsam, da das Produkt unbekannt ist und am Ende ist das Wachstum langsam, weil der Markt gesättigt ist.
-
Infektionszahlen: Am Beginn ist das Wachstum langsam, da erst wenige Meschen ansteckend sind und am Ende ist das Wachstum langsam, weil die Ausbreitung durch die hohe Immunität erschwert wird.
-
Populationen mit beschränkten Ressourcen (z. B. Insel): Am Beginn ist das Wachstum langsam, da wenige Individuen für die Vermehrung verfügbar sind und am Ende ist das Wachstum langsam, weil die Ressourcen knapp werden.
Wie sieht der Graph einer logistischen Funktion aus? Markiere alle wichtigen Eigenschaften!
Wie erstellt man anhand passender Vorgaben die Gleichung einer logistischen Funktion?
Lösung zeigen
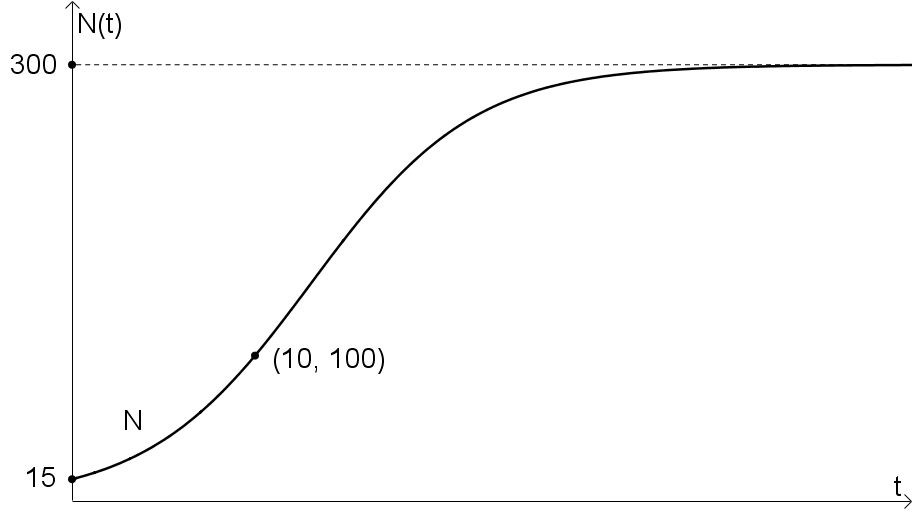
Beispiel: Es soll die Funktionsgleichung zur folgenden Abbildung erstellt werden.
Die allgemeine Form der Funktionsgleichung sieht folgendermaßen aus:
N(t)=S1+c⋅at
-
Es wird die Schranke ermittelt. In diesem Beispiel gilt S=300. Bei Textaufgaben ist die Schranke meistens in der Aufgabenstellung enthalten.
-
Als Nächstes wird der Anfangswert N0 bestimmt. In diesem Beispiel gilt N0=15. Bei Textaufgaben ist auch dieser Wert meistens in der Aufgabenstellung enthalten.
-
Mittels c=S−N0N0 wird nun der Parameter c berechnet. In diesem Beispiel erhält man c=300−1515=19.
-
Nun benötigt man einen Punkt des Funktionsgraphen, hier (10∣100). Häufig ist bei Textaufgaben ein Wertepaar in der Aufgabenstellung enthalten.
-
Zuletzt werden alle bekannten Werte in die obige Grundgleichung eingesetzt, um damit a zu berechnen:
100=3001+19⋅a10 ⇒ a=10√300100−119≈0,7984
-
Die Funktionsgleichung lautet N(t)=3001+19⋅0,7984t