Fragen
Allgemeine Aufgaben
Wie lautet die Grundgleichung einer linearen Funktion?
Welche Bedeutung haben die Parameter $k$ und $d$ in der Funktionsgleichung $f(x)=k\cdot x +d$?
Wie sieht der Graph einer linearen Funktion aus?
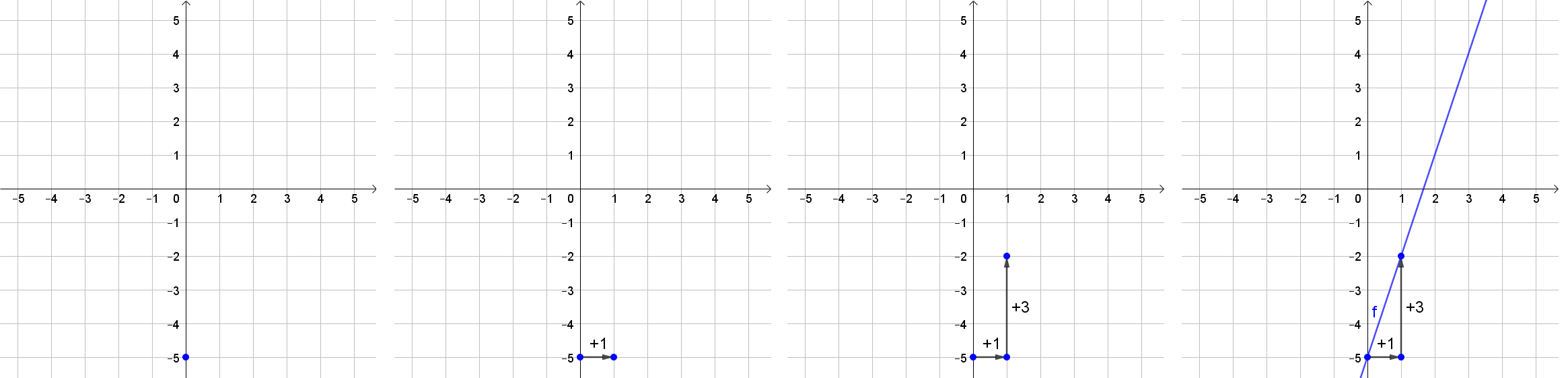
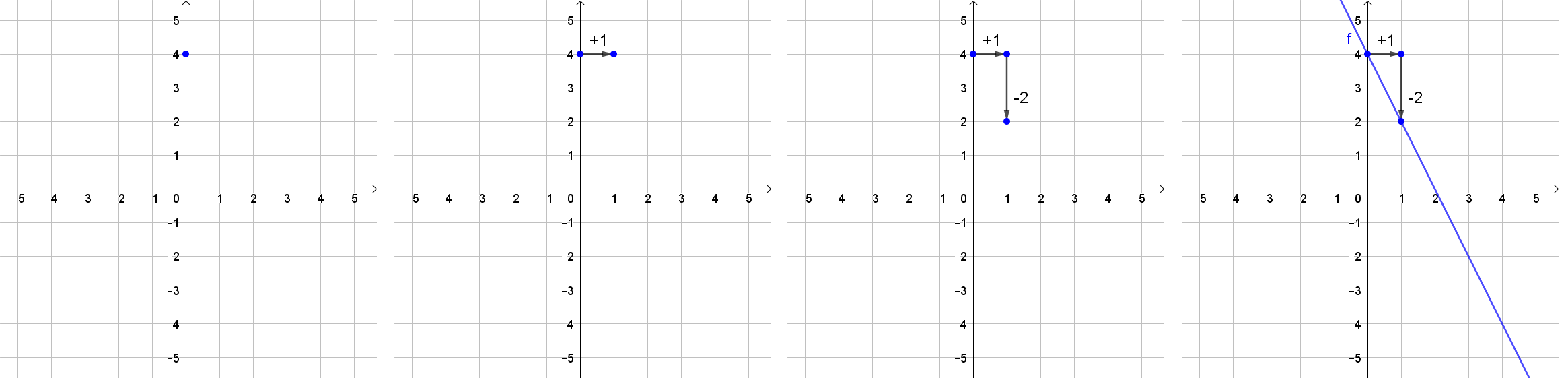
Wie zeichnet man den Graphen einer linearen Funktion, wenn die Funktionsgleichung bekannt ist und die Steigung ganzzahlig ist? Demonstriere anhand eines Beispiels!
Lösung zeigen
-
Es wird beim Ordinatenabschnitt ein Punkt gezeichnet.
-
Von diesem Punkt geht man 1 nach rechts.
-
Nun geht man so weit nach oben/unten, bis man den Wert der Steigung erreicht hat (bei $k=2$ geht man 2 nach oben, bei $k=-5$ geht man 5 nach unten).
-
Abschließend wird eine Gerade durch Anfangspunkt und Endpunkt gezeichnet (nicht bei den Punkten aufhören, sondern darüber hinaus zeichnen).
Beispiel 1: $f(x)=3x-5$
Beispiel 2: $f(x)=4-2x$
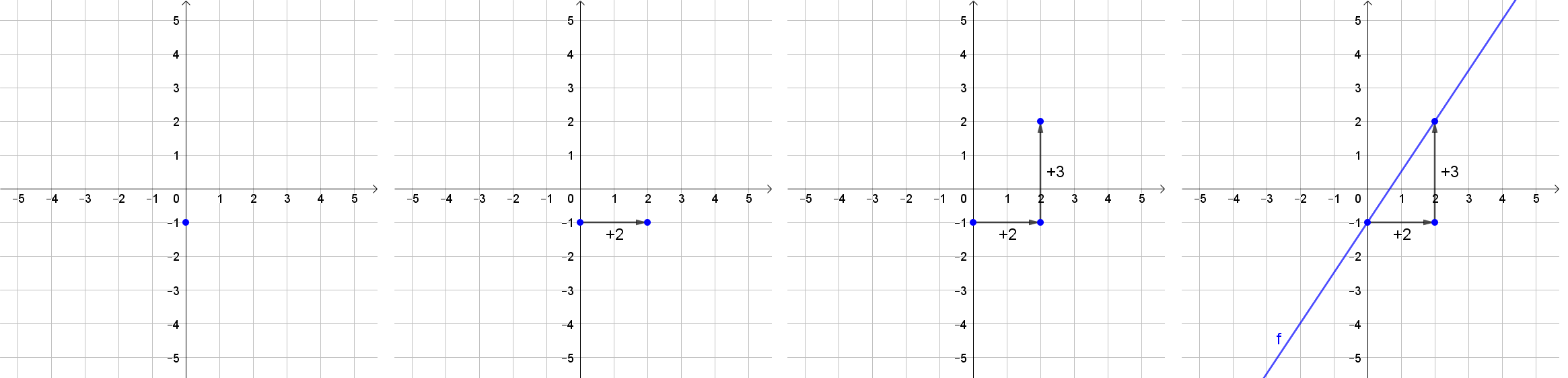
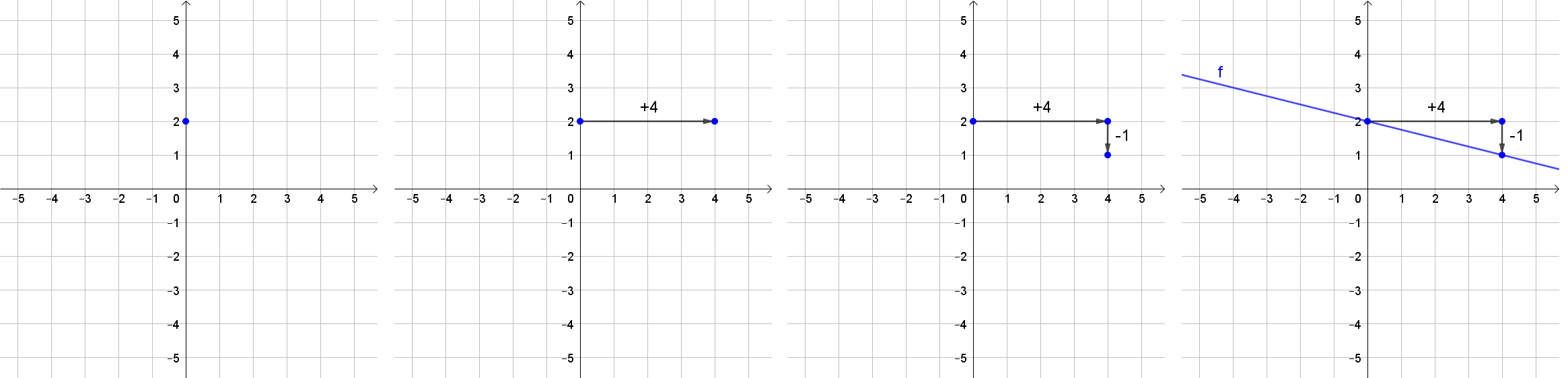
Wie zeichnet man den Graphen einer linearen Funktion, wenn die Funktionsgleichung bekannt ist und die Steigung einem Bruch entspricht? Demonstriere anhand eines Beispiels!
Lösung zeigen
-
Es wird beim Ordinatenabschnitt ein Punkt gezeichnet.
-
Von diesem Punkt aus geht man den Nenner der Steigung ($\Delta x$) nach rechts.
-
Nun geht man den Zähler der Steigung ($\Delta y$) nach oben bzw. unten (je nach Vorzeichen der Steigung).
-
Abschließend wird eine Gerade durch Anfangspunkt und Endpunkt gezeichnet (nicht bei den Punkten aufhören, sondern darüber hinaus zeichnen).
Beispiel 1: $f(x)=\frac{3}{2}\cdot x -1$
Beispiel 2: $f(x)=2-\frac{x}{4}$
Welchen Einfluss hat der Ordinatenabschnitt auf den Funktionsgraphen einer linearen Funktion?
Lösung zeigen
-
Ist $d>0$, so wird die $y$-Achse oberhalb der $x$-Achse geschnitten.
-
Ist $d=0$, so verläuft der Funktionsgraph durch den Koordinatenursprung.
-
Ist $d<0$, so wird die $y$-Achse unterhalb der $x$-Achse geschnitten.
Welchen Einfluss hat die Steigung auf den Funktionsgraphen einer linearen Funktion?
Lösung zeigen
-
Ist $k>0$, so ist die Gerade nach rechts ansteigend.
-
Ist $k=0$, so ist die Gerade waagrecht (parallel zur $x$-Achse).
-
Ist $k<0$, so ist die Gerade nach rechts abfallend.
Wie viele Schnittpunkte können zwei lineare Funktionen haben und wovon hängt dies ab?
Lösung zeigen
-
Falls die Steigungen unterschiedlich sind, haben sie immer genau einen Schnittpunkt.
-
Falls die Steigungen gleich sind, jedoch die Ordinatenabschnitte verschieden sind, haben sie keinen Schnittpunkt.
-
Falls die Steigungen und die Ordinatenabschnitte gleich sind, haben sie unendlich viele Schnittpunkte (die Geraden sind deckungsgleich).
Wie wird der Schnittpunkt zweier linearer Funktionen berechnet? Demonstriere anhand eines Beispiels!
Lösung zeigen
Beispiel: $f(x)=2x+1$, $g(x)=-\frac{x}{2} +6$
-
Es werden die Funktionsterme gleichgesetzt, also $2x+1=-\frac{x}{2} +6$.
-
Es wird die Gleichung nach $x$ gelöst: $2x+1=-\frac{x}{2} +6 \Rightarrow 2{,}5x = 5 \Rightarrow x=2$.
-
Für den $y$-Wert wird in eine der beiden Funktionen eingesetzt: $f(2)=2\cdot 2+1 = 5$.
-
Der Schnittpunkt lautet $(2\mid 5)$.
Welchen Ordinatenabschnitt hat die Funktion mit der Gleichung $f(x)=3x$?
Welche Steigung hat die Funktion mit der Gleichung $f(x)=-x+3$?
Welche Steigung hat die Funktion mit der Gleichung $f(x)=x+3$?
Wie viele Nullstellen haben lineare Funktionen?
Wie wird die Nullstelle einer linearen Funktion berechnet? Demonstriere anhand eines Beispiels!
Lösung zeigen
Beispiel: $f(x)=-1{,}2x+6$
Zur Berechnung von Nullstellen muss die Gleichung $f(x)=0$ gelöst werden. Für dieses Beispiel erhält man $0=-1{,}2x+6 \Rightarrow 1{,}2x = 6 \Rightarrow x=5$.
Wofür steht das Symbol $\Delta$ (z. B. $\Delta y$)?
Lösung zeigen
Das Symbol $\Delta$ ist der griechische Großbuchstabe Delta und beschreibt meist einen Abstand zwischen zwei Werten. Beispielsweise ist $\Delta y$ der $y$-Abstand zwischen zwei Punkten.
einklappen
Mit welcher Formel kann die Steigung zwischen zwei Punkten ermittelt werden?
Wie kann die Funktionsgleichung einer linearen Funktion durch zwei Punkte bestimmt werden? Demonstriere anhand eines Beispiels!
Lösung zeigen
Beispiel: $A(-3\mid 4)$, $B(2 \mid 1)$
-
Es wird die Steigung mittels $k=\frac{y_2-y_1}{x_2-x_1}$ ermittelt. Man erhält $k=\frac{1-4}{2-(-3)} = \frac{-3}{5}=-0{,}6$.
-
Es wird die Steigung und einer der beiden Punkte in die Grundgleichung $y=k\cdot x+d$ eingesetzt und nach $d$ umgeformt (hier wurde Punkt $B$ gewählt): $1 = -0{,}6\cdot 2 +d \Rightarrow d = 1+ 0{,}6\cdot 2 =2{,}2$.
-
Die Funktionsgleichung lautet daher $f(x)=-0{,}6x+2{,}2$.
Wie überprüft man, ob bei einer vorgegebenen Liste von Punkten ein linearer Zusammenhang besteht? Demonstriere anhand eines Beispiels!
Lösung zeigen
Damit ein linearer Zusammenhang besteht, müssen alle Punkte auf einer Gerade liegen. Das bedeutet, dass die Steigung zwischen allen Punkten gleich sein muss. Man setzt daher der Reihe nach jeweils zwei aufeinanderfolgende Punkte in der Formel $\frac{y_2 -y_1}{x_2-x_1}$ ein. Falls alle Ergebnisse gleich sind, ist der Zusammenhang linear, sonst nicht.
Beispiel: $A(2\mid 3), B(6\mid 9), C(8\mid 13)$
$$k_1 = \frac{9-3}{6-2} = 1{,}5\hspace{15mm} k_2 = \frac{13-9}{8-6} = 2$$
Da die Steigungen nicht gleich sind, handelt es sich bei den drei vorgegebenen Punkten um keinen linearen Zusammenhang.
Parallele und normale Geraden
Wie erkennt man anhand der Funktionsgleichungen, dass zwei Geraden normal zueinander sind? Gib ein Beispiel!
Lösung zeigen
Die Steigungen sind die negativen Kehrwerte zueinander, also $k_1 = -\frac{1}{k_2}$.
Beispiel: $f_1(x)=2x+3$ und $f_2(x)=-0{,}5x-1$, denn $-\frac{1}{2} = -0{,}5$ bzw. $-\frac{1}{-0{,}5} = 2$.
Wie erkennt man anhand der Funktionsgleichung, ob zwei lineare Funktionen parallel sind?
