| Fragen
Wie wird die Eulersche Zahl $e$ auf deinem Taschenrechner eingegeben?
Lösung zeigen
Die Eingabe ist abhängig vom Taschenrechner. Das Ergebnis sollte ca. $2{,}718281828$ sein. einklappen
Wie lauten die ersten zehn signifikanten Stellen der Eulerschen Zahl $e$ und wie kann man sich diese leicht merken?
Lösung zeigen
$e = 2{,}718281828...$
Auffallend ist die Ziffernfolge 18-28-18-28 anhand welcher man sich die ersten zehn signifikanten Stellen dieser Zahl relativ gut merken kann. einklappen
Wie kann man die Eulersche Zahl $e$ definieren?
Lösung zeigen
Eine mögliche Definition ist durch folgende unendliche Summe gegeben:
$\sum_{k=0}^\infty \frac{1}{k!} = \frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\frac{1}{4!}+... = \frac{1}{1}+\frac{1}{1}+\frac{1}{1\cdot 2}+\frac{1}{1\cdot 2\cdot 3}+\frac{1}{1\cdot 2\cdot 3\cdot 4}+...$ einklappen
Exponentialfunktion
Wie lautet die Grundgleichung einer Exponentialfunktion und welche Bedingungen müssen erfüllt sein?
Wie erkennt man, ob eine Exponentialfunktion steigend oder fallend ist, wenn die Gleichung in der Form $f(x)=c\cdot a^x$ gegeben ist? Gib Beispiele!
Lösung zeigen
Entscheidend ist hierfür der Änderungsfaktor $a$:
-
Falls $a>1$ gilt, ist die Funktion steigend. Beispiel: $f(x)=0{,}3 \cdot 2{,}5^x$
-
Falls $0< a<1$ gilt, ist die Funktion fallend. Beispiel: $f(x)=6 \cdot 0{,}8^x$
-
Falls $a=1$ gilt, ist die Funktion konstant (dieser Fall wird meistens nicht als Exponentialfunktion bezeichnet). Beispiel: $f(x)=2\cdot 1^x = 2$
einklappen
Welchen Einfluss hat bei der Funktionsgleichung $f(x)=c\cdot a^x$ der Parameter $c$ auf den Funktionsgraphen einer Exponentialfunktion?
Lösung zeigen
Der Parameter $c$ gibt an, bei welchem Wert die $y$-Achse geschnitten wird (Ordinatenabschnitt).
Begründung: $f(0)=c\cdot a^0 = c\cdot 1=c$ einklappen
Wie kann die Funktionsgleichung einer Exponentialfunktion anhand des Funktionsgraphen bestimmt werden? Demonstriere anhand eines Beispiels!
Lösung zeigen
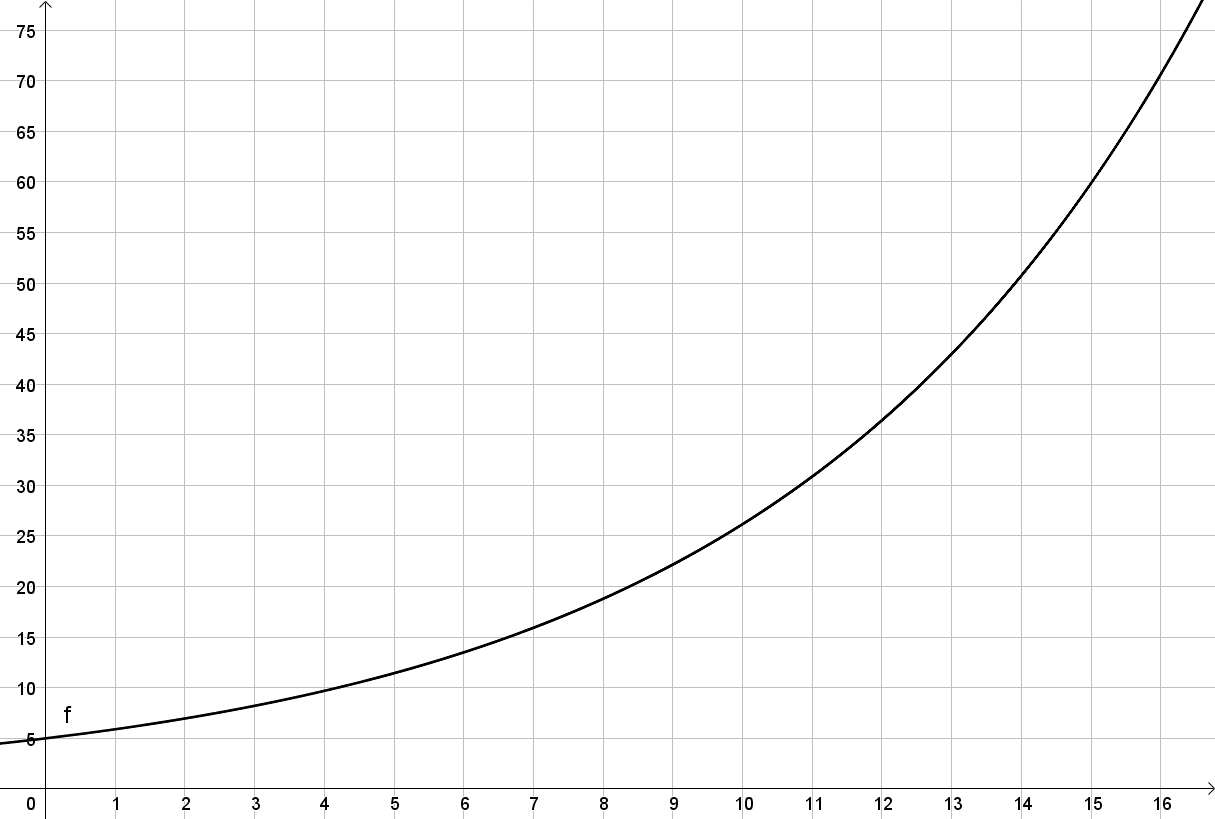
Als Beispiel wird folgender Funktionsgraph verwendet:
-
Man liest den Ordinatenabschnitt $c=5$ ab.
-
Man sucht einen Punkt des Funktionsgraphen, der möglichst exakt auf einem Gitterpunkt des Koordinatensystems liegt. Hier eignet sich der Punkt $(15\mid 60)$.
-
Man setzt den Ordinatenabschnitt und die Koordinaten des ausgewählten Punktes in die Grundgleichung $y=c\cdot a ^x$ ein und erhält $60 = 5\cdot a^{15}$.
-
Durch Lösen der Gleichung erhält man den Änderungsfaktor $a$. Das Ergebnis lautet $a= \sqrt[15]{\frac{60}{5}} = \sqrt[15]{12} \approx 1{,}1802$.
-
Die Funktionsgleichung lautet $f(x)\approx 5 \cdot 1{,}1802^x$.
einklappen
Wie kann die Funktionsgleichung einer Exponentialfunktion durch zwei Punkte bestimmt werden? Demonstriere anhand eines Beispiels!
Lösung zeigen
Beispiel: $A(-3\mid 2)$, $B(5 \mid 8)$
-
Es werden die Koordinaten beider Punkte in die Grundgleichung $y=c\cdot a^x$ eingesetzt, wodurch ein Gleichungssystem mit den Gleichungen $2=c\cdot a^{-3}$ und $8 =c\cdot a^5$ entsteht.
-
Es wird eine der beiden Gleichungen nach $c$ umgeformt: $2=c\cdot a^{-3} ~ \Rightarrow ~ c= \frac{2}{a^{-3}} = 2\cdot a^3$.
-
Das Resultat wird anstelle von $c$ in die andere Gleichung eingesetzt: $8 = 2\cdot a^3 \cdot a^5 = 2\cdot a^8$.
-
Durch Lösen der Gleichung wird $a$ ermittelt: $a= \sqrt[8] {\frac{8}{2}} = \sqrt[8] {4} \approx 1{,}1892$.
-
Abschließend wird in die Formel für $c$ (aus Punkt 2) eingesetzt: $c=2\cdot a^3 \approx 2 \cdot 1{,}1892^3 \approx 3{,}3635$.
-
Die Funktionsgleichung lautet $f(x)\approx 3{,}3635\cdot 1{,}1892^x$.
einklappen
Wie erkennt man, ob eine Exponentialfunktion steigend oder fallend ist, wenn die Gleichung in der Form $f(x)=c\cdot e^{\lambda \cdot x}$ gegeben ist? Gib Beispiele!
Lösung zeigen
Entscheidend ist hierfür der Parameter $\lambda$:
-
Falls $\lambda > 0$ gilt, ist die Funktion steigend. Beispiel: $f(x)=0{,}3 \cdot e^{0{,}8 \cdot x}$
-
Falls $\lambda < 0$ gilt, ist die Funktion fallend. Beispiel: $f(x)=5 \cdot e^{-1{,}2 \cdot x}$
einklappen
Wie erfolgt die Umrechnung zwischen den Formen $f(x)=c\cdot a^x$ und $f(x)=c\cdot e^{\lambda \cdot x}$ der Funktionsgleichung einer Exponentialfunktion? Demonstriere anhand von Beispielen!
Lösung zeigen
Allgemeine Formeln: $a=e^\lambda$ und $\lambda =\ln(a)$
Herleitung:
-
Da beide Terme äquivalent sein müssen, muss die Gleichung $c\cdot a^x = c\cdot e^{\lambda \cdot x}$ erfüllt sein.
-
Nach Division durch den Faktor $c$ bleibt $a^x = e^{\lambda \cdot x}$ übrig.
-
Setzt man $x=1$ ein, so erhält man $a=e^\lambda$. Damit ist die Herleitung der ersten Formel abgeschlossen.
-
Wird auf beiden Seiten der natürliche Logarithmus angewendet, so erhält man $\ln(a) = \lambda \cdot \ln(e)$.
-
Wegen $\ln(e)=1$ reduziert sich die Gleichung auf $\ln(a) = \lambda$, wodurch auch die zweite Formel hergeleitet wurde.
Beispiel 1: $f(x)=3\cdot 1{,}2^x \Rightarrow f(x)=3\cdot e^{0{,}1823x}$, Nebenrechnung: $\ln(1{,}2) \approx 0{,}1823$
Beispiel 2: $f(x)=2\cdot e^{-0{,}85x} \Rightarrow f(x)=2\cdot 0{,}4274^x$, Nebenrechnung: $e^{-0{,}85} \approx 0{,}4274$ einklappen
|
