| Fragen Änderungsmaße
Welche Änderungsmaße für Funktionen gibt es?
Lösung zeigen
Es können folgende Änderungsmaße berechnet werden:
-
absolute Änderung
-
relative Änderung
-
prozentuelle Änderung
-
mittlere/durchschnittliche Änderungsrate
-
momentane/lokale Änderungsrate
einklappen
Was ist der unterschied zwischen einer Änderung und einer Änderungsrate?
Lösung zeigen
Für eine Änderung wird nur der Unterschied der Funktionswerte $\Delta y$ herangezogen (die Veränderung der unabhängigen Variable $x$ spielt keine Rolle).
Bei Änderungsraten wird ein Verhältnis zwischen $\Delta y$ und $\Delta x$ ermittelt. Es wird also berechnet, wie sich eine Änderung der unabhängigen Variable $x$ auf die abhängige Variable $y$ auswirkt. einklappen
Wie wird die absolute Änderung einer Funktion $f$ im Intervall $[a; b]$ berechnet, was kann man sich darunter vorstellen und welche Einheit hat sie?
Lösung zeigen
Formel: $f(b)-f(a)$
Bedeutung: Sie beschreibt, um welchen Wert sich die Funktion in diesem Intervall insgesamt ändert.
Einheit: Die absolute Änderung besitzt dieselbe Einheit wie die Funktion $f$ selbst. einklappen
Wie wird die relative Änderung einer Funktion $f$ im Intervall $[a; b]$ berechnet, was kann man sich darunter vorstellen (inkl. Beispiele) und welche Einheit hat sie?
Lösung zeigen
Formel: $\frac{f(b)-f(a)}{f(a)}$
Bedeutung: Sie beschreibt, um welchen Anteil des Anfangswertes $f(a)$ sich die Funktion insgesamt verändert. Beträgt die relative Änderung $\frac{1}{3}$, so ist die Funktion um ein Drittel ihres Anfangswertes gestiegen. Beträgt sie hingegen $-\frac{1}{4}$, so ist die Funktion um ein Viertel ihres Anfangswertes gesunken.
Einheit: Die relative Änderung besitzt keine Einheit (diese wird gekürzt, da Zähler und Nenner dieselbe Einheit besitzen). einklappen
Wie wird die prozentuelle Änderung einer Funktion $f$ im Intervall $[a;b]$ berechnet und was kann man sich darunter vorstellen (inkl. Beispiele)?
Lösung zeigen
Formel: $\frac{f(b)-f(a)}{f(a)} \cdot 100\,\%$
Die prozentuelle Änderung entspricht im Wesentlichen der relativen Änderung. Sie wird jedoch in Prozent angegeben. Beträgt die prozentuelle Änderung beispielsweise 20 %, so ist der Wert der Funktion um 20 % gestiegen. Beträgt sie hingegen -35 %, so ist der Wert um 35 % gesunken. einklappen
Wie wird die mittlere Änderungsrate einer Funktion $f$ im Intervall $[a; b]$ berechnet, was kann man sich darunter vorstellen, welche anderen Bezeichnungen gibt es dafür und welche Einheit hat sie?
Lösung zeigen
Formel: $\frac{f(b)-f(a)}{b-a}$
Bedeutung: Sie beschreibt, wie sich die Funktion pro Einheit der $x$-Achse durchschnittlich ändert. Ist ihr Wert beispielsweise 3, so steigt die Funktion durchschnittlich um 3 Einheiten, wenn die unabhängige Variable $x$ um eine Einheit vergrößert wird.
Alternativbezeichnungen: Die mittlere Änderungsrate wird auch durchschnittliche Änderungsrate bzw. Differenzenquotient genannt.
Einheit: Ihre Einheit entspricht der Einheit der Funktion dividiert durch die Einheit der unabhängigen Variable $x$. Wird beispielsweise $f(x)$ in °C gemessen und $x$ in Minuten, so ist die Einheit der mittleren Änderungsrate °C/min. einklappen
Wie wird die momentane Änderungsrate einer Funktion $f$ an der Stelle $a$ berechnet, was kann man sich darunter vorstellen, welche anderen Bezeichnungen gibt es dafür und welche Einheit hat sie?
Lösung zeigen
Formel: $\lim \limits_{b \to a} \frac{f(b)- f(a)}{b - a}$
Bedeutung: Sie entspricht dem Grenzwert einer mittleren Änderungsrate, bei welcher die obere Intervallgrenze $b$ immer weiter an die untere Intervallgrenze $a$ angenähert wird.
Alternativbezeichnungen: Die momentane Änderungsrate wird auch lokale Änderungsrate bzw. Differentialquotient genannt. Sie entspricht der ersten Ableitung $f'$ der Funktion $f$.
Einheit: Die Einheit ist dieselbe wie jene der mittleren Änderungsrate, also Einheit der Funktion dividiert durch Einheit der unabhängigen Variable $x$. einklappen
Ableitungsfunktion
Welche Bedeutung hat die Ableitungsfunktion einer Funktion $f$?
Lösung zeigen
Mit der Ableitungsfunktion kann für jede beliebige Stelle $x$ die momentane Änderungsrate der Funktion $f$ berechnet werden. einklappen
Welche Schreibweise wird für die Ableitungsfunktion der Funktion $f$ verwendet?
Wie werden Potenzfunktionen abgeleitet? Gib konkrete Beispiele und nenne die allgemeine Regel für die Ableitungsfunktion von $f(x)=x^n$.
Lösung zeigen
Die aktuelle Hochzahl kommt vor die Potenz und die neue Hochzahl ist um 1 kleiner.
Beispiel 1: $f(x)=x^3 \Rightarrow f'(x)=3x^2$
Beispiel 2: $f(x)=x^5 \Rightarrow f'(x)=5x^4$
allgemeine Regel: $f(x)=x^n \Rightarrow f'(x)=n \cdot x^{n-1}$ einklappen
Wie wird die Funktionsgleichung $f(x)=\frac{1}{x^3}$ abgeleitet?
Lösung zeigen
Zunächst wird die Gleichung umgeformt zu $f(x)=x^{-3}$. Dies ist noch nicht die Ableitungsfunktion, sondern nur eine andere Schreibweise der ursprünglichen Funktion!
Nun wird die Potenzregel angewendet und abschließend wieder mit positiver Hochzahl geschrieben: $f'(x)=-3\cdot x^{-4}=-\frac{3}{x^4}$
Achtung: Bei der Potenzregel wird die Hochzahl um 1 verkleinert, also $-3 -1=-4$. Häufig wird hier fälschlicherweise $-2$ geschrieben, da man intuitiv glauben könnte, dass $-2$ um 1 kleiner ist als $-3$. einklappen
Wie wird die Funktionsgleichung $f(x)=\sqrt{x}$ abgeleitet?
Lösung zeigen
Zunächst wird der Funktionsterm in Potenzschreibweise dargestellt, also $f(x)=x^\frac{1}{2}$.
Jetzt wird die Potenzregel verwendet: $f'(x)=\frac{1}{2}\cdot x^{-\frac{1}{2}} $
Zuletzt wird der Term wieder ohne negativen Exponent und mittels Wurzel dargestellt: $f'(x)=\frac{1}{2\cdot \sqrt{x}}$ einklappen
Wie lautet die Ableitung von $f(x)=x$. Gib eine Begründung dafür!
Lösung zeigen
Für $f(x)=x$ gilt $f'(x)=1$.
Begründung 1: Die Funktionsgleichung $f(x)=x$ entspricht einer Gerade mit Steigung 1. Daher hat die Ableitungsfunktion überall den Wert 1.
Begründung 2: Man kann den Funktionsterm auch als Potenz schreiben: $f(x)=x^1$. Durch Anwenden der Potenzregel erhält man $f'(x)=1\cdot x^0$. Weil $x^0=1$ gilt, erhält man $f'(x)=1$. einklappen
Wie lautet die Ableitung der konstanten Funktion $f(x)=c$ mit $c\in \mathbb{R}$. Gib eine Begründung dafür!
Lösung zeigen
Es gilt $f'(x)=0$.
Begründung 1: Die konstante Funktion entspricht einer waagrechten Gerade. Die Steigung (also die 1. Ableitung) hat daher überall den Wert 0.
Begründung 2: Man könnte die Funktionsgleichung $f(x)=c$ ergänzen zu $f(x)=c\cdot x^0$, denn $x^0 =1$ und eine Multiplikation mit 1 verändert den Wert des Terms nicht. Durch die Potenzregel ergibt sich $f'(x)=c\cdot 0\cdot x^{-1}=0$. einklappen
Wie lautet die Ableitungfunktion von $f(x)=e^x$?
Lösung zeigen
Die Ableitung ist identisch mit der ursprünglichen Funktion: $f(x)=e^x \Rightarrow f'(x)=e^x$ einklappen
Für welche Funktionen gilt $f(x)=f'(x)$?
Lösung zeigen
Die Funktionsgleichungen $f(x)=0$ und $f(x)=e^x$ bleiben durch das Bilden der Ableitung unverändert. einklappen
Wie lautet die Summenregel beim Ableiten von Funktionen? Demonstriere die Anwendung anhand eines Beispiels!
Lösung zeigen
Allgemeine Regel: $f(x)=f_1(x)\pm f_2(x) \,\Rightarrow \, f'(x)=f_1'(x) \pm f_2'(x)$
Verbale Beschreibung: Besteht ein Funktionsterm aus der Summe bzw. Differenz mehrerer Terme, so kann jeder Term getrennt abgeleitet werden.
Beispiel: $f(x)=4x^3 - 5x^2+8x \,\Rightarrow \, f'(x)=12x^2-10x+8$ einklappen
Wie lautet die Produktregel beim Ableiten von Funktionen? Demonstriere die Anwendung anhand eines Beispiels!
Lösung zeigen
Allgemeine Regel: $f(x)=f_1(x)\cdot f_2(x)\,\Rightarrow\, f'(x)=f_1'(x)\cdot f_2(x)+ f_1(x)\cdot f_2'(x)$
Verbale Beschreibung: Zunächst wird der erste Faktor abgeleitet und der zweite Faktor bleibt unverändert. Anschließend bleibt der erste Faktor unverändert und der zweite Faktor wird abgeleitet. Da in der Formel ein Plus vorkommt, ist es unwichtig, welcher der beiden Faktoren zuerst abgeleitet wird. Die Produktregel muss nur verwendet werden, wenn beide Faktoren die Variable enthalten.
Beispiel: $f(x)=x^2 \cdot \sin(x) \,\Rightarrow\, f'(x)=2x\cdot \sin(x) + x^2\cdot \cos(x)$ einklappen
Zeige anhand eines Beispiels, warum beim Ableiten von Produkten nicht einfach jeder Faktor getrennt abgeleitet werden kann!
Lösung zeigen
Beispiel: $f(x)=x^2\cdot x^3$
Diese Funktionsgleichung kann zu $f(x)=x^5$ zusammengefasst werden. Durch die Potenzregel ist daher bekannt, dass die Ableitungsfunktion die Gleichung $f'(x)=5x^4$ besitzen muss.
Würde man beide Faktoren getrennt voneinander ableiten, so würde man folgendes Resultat erhalten: $f'(x)=2x\cdot 3x^2=6x^3$. Somit ist gezeigt, dass diese Vorgehensweise falsch ist. einklappen
Welche Möglichkeiten gibt es, um die Ableitung von $f(x)=3x^2 \cdot (5x+10)$ zu bestimmen?
Lösung zeigen
1. Möglichkeit: Man verwendet die Produktregel.
2. Möglichkeit: Man löst die Klammer durch Ausmultiplizieren auf und verwendet die Summenregel. einklappen
Wie lautet die Quotientenregel beim Ableiten von Funktionen? Demonstriere die Anwendung anhand eines Beispiels!
Lösung zeigen
Allgemeine Regel: $f(x)=\frac{f_1(x)}{f_2(x)} \,\Rightarrow \, f'(x)=\frac{f_1'(x)\cdot f_2(x) - f_1(x)\cdot f_2'(x)}{\left( f_2(x)\right)^2}$
Achtung: Im Vergleich zur Produktregel ist hier aufgrund des Minus die Reihenfolge wichtig!
Beispiel: $f(x)=\frac{5x^2}{3x-2}\,\Rightarrow \, f'(x)=\frac{10x\cdot (3x-2) - 5x^2 \cdot 3}{(3x-2)^2} = \frac{15x^2-20x}{(3x-2)^2}$ einklappen
Wie lautet die Kettenregel beim Ableiten von Funktionen? Demonstriere die Anwendung anhand eines Beispiels!
Lösung zeigen
Allgemeine Regel: $f(x)=f_1(f_2(x))\,\Rightarrow\, f'(x)=f_1'(f_2(x)) \cdot f_2'(x)$
Verbale Beschreibung: Die Kettenregel wird verwendet, um verschachtelte Funktionen abzuleiten. Zunächst wird die äußere Funktion abgeleitet und die innere Funktion bleibt unverändert (man spricht von der „äußeren Ableitung“). Anschließend wird mit der Ableitung der inneren Funktion multipliziert (man spricht von der „inneren Ableitung“).
Beispiel: $f(x)=(5x^2-3x+10)^4\,\Rightarrow\, f'(x)=4\cdot (5x^2-3x+10)^3 \cdot (10x-3)$ einklappen
Wie erkennt man bei der Kettenregel, was die äußere und was die innere Funktion ist? Gib passende Beispiele!
Lösung zeigen
Üblicherweise ist die innere Funktion jener Term, in welchem die Variable $x$ vorkommt.
Beispiel 1: $f(x)=\sqrt{x^2+1}$ ... Hier ist die Wurzel $\sqrt{...}$ die äußere Funktion und $x^2+1$ die innere Funktion.
Beispiel 2: $f(x)=(4x-5)^3$ ... Hier ist die Potenz $(...)^3$ die äußere Funktion und $4x-5$ die innere Funktion.
Beispiel 3: $f(x)=\sin(2x+3)$ ... Hier ist der Sinus $\sin(...)$ die äußere Funktion und $2x+3$ die innere Funktion.
Beispiel 4: $f(x)=e^{x^2-3}$ ... Hier ist die Exponentialfunktion $e^{...}$ die äußere Funktion und $x^2-3$ die innere Funktion. einklappen
Tangente und Sekante
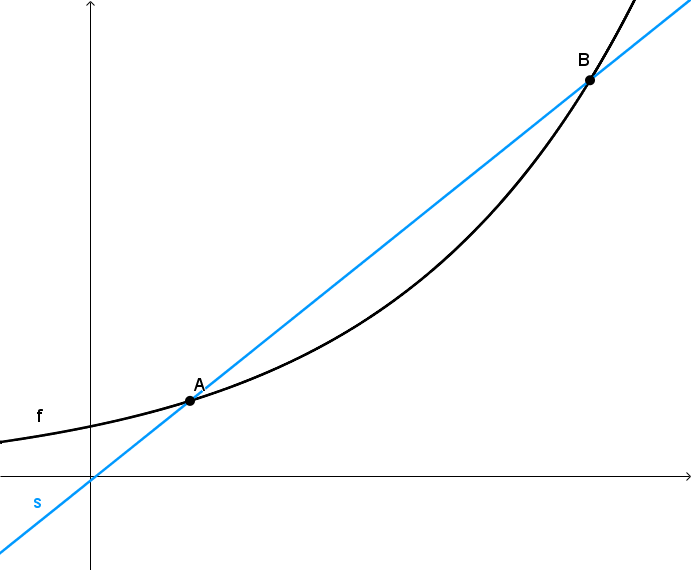
Was ist eine Sekante einer Funktion? Erstelle eine Skizze und gib die allgemeine Funktionsgleichung an!
Lösung zeigen
Eine Sekante ist eine Gerade, die durch zwei Punkte des Funktionsgraphen einer Funktion verläuft. Ihre Funktionsgleichung entspricht jener einer linearen Funktion, also $s(x)=k\cdot x+d$.
einklappen
Wie wird die Sekantengleichung einer Funktion für ein vorgegebenes Intervall erstellt? Demonstriere anhand eines Beispiels!
Lösung zeigen
Beispiel: Es soll zur Funktionsgleichung $f(x)=-\frac{x^2}{2}+4$ die Sekantengleichung für das Intervall $[-2; 3]$ bestimmt werden.
-
Es werden die Funktionswerte an den Intervallgrenzen berechnet: $f(-2)=2,~~f(3)=-0{,}5$.
-
Es wird die mittlere Steigung (Differenzenquotient) für dieses Intervall berechnet: $\frac{y_2-y_1}{x_2-x_1}=\frac{-0{,}5 - 2}{3-(-2)} = -0{,}5$.
-
Es werden die soeben berechnete Steigung und die Koordinaten von einem der beiden Punkte in die Grundgleichung $s(x)=k\cdot x+d$ eingesetzt: $2=-0{,}5\cdot (-2)+d$.
-
Es wird $d$ berechnet: $d=2-(-0{,}5)\cdot (-2)=1$.
-
Die Sekantengleichung lautet $s(x)=-0{,}5x+1$.
einklappen
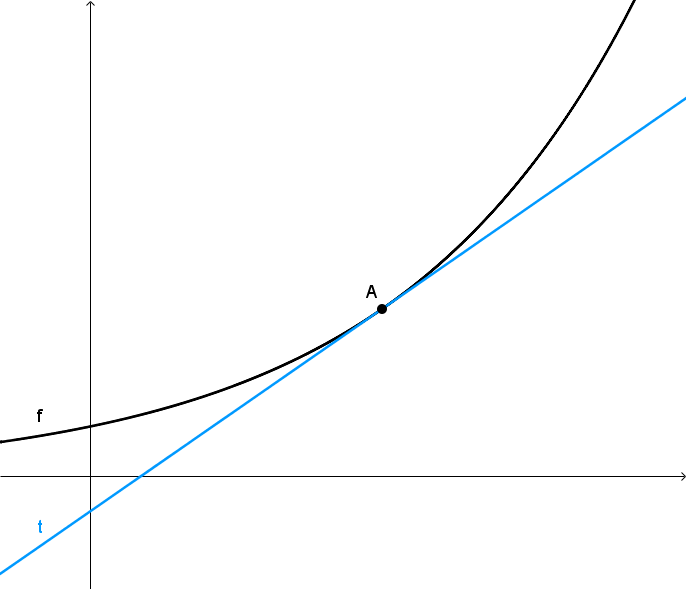
Was ist eine Tangente einer Funktion? Erstelle eine Skizze und gib die allgemeine Funktionsgleichung an!
Lösung zeigen
Eine Tangente ist eine Gerade, die durch einen Punkt des Funktionsgraphen einer Funktion verläuft und dort dieselbe Steigung besitzt, wie die Funktion selbst. Ihre Funktionsgleichung entspricht jener einer linearen Funktion, also $t(x)=k\cdot x+d$.
einklappen
Wie wird die Tangentengleichung einer Funktion zu einer vorgegebenen Stelle erstellt? Demonstriere anhand eines Beispiels!
Lösung zeigen
Beispiel: Es soll zur Funktionsgleichung $f(x)=2x^2+5$ die Tangentengleichung für die Stelle $x=3$ bestimmt werden.
-
Es wird die Ableitungsfunktion $f'$ bestimmt: $f'(x)=4x$.
-
Es wird der Funktionswert und die Steigung an der vorgegebenen Stelle berechnet: $f(3)=2\cdot 3^2+5=23,~~ f'(3)=4\cdot 3=12$.
-
Es werden alle bekannten Werte in die Tangentengleichung $t(x)=k\cdot x+d$ eingesetzt: $23=12\cdot 3+d$.
-
Es wird $d$ berechnet: $d=23-12\cdot 3 = -13$.
-
Die Tangentengleichung lautet $t(x)=12 x-13$.
einklappen
Was ist eine Wendetangente und wie wird ihre Gleichung bestimmt?
Lösung zeigen
Eine Wendetangente ist eine Tangente, die durch einen Wendepunkt einer Funktion verläuft. Ihre Gleichung wird grundsätzlich genauso bestimmt, wie von jeder anderen Tangente. Jedoch ist die Stelle meistens nicht vorgegeben. Es muss als im ersten Schritt berechnet werden, an welcher Stelle sich der Wendepunkt befindet. einklappen
Bewegungsaufgaben
Wie hängen Weg-, Geschwindigkeits- und Beschleunigungsfunktion zusammen?
Lösung zeigen
Die Geschwindigkeit ist die Ableitung des Weges, also $v(t)=s'(t)$.
Die Beschleunigung ist die Ableitung der Geschwindigkeit, also $a(t)=v'(t)=s''(t)$. einklappen
Wie lautet die Standardeinheit der Beschleunigung und was kann man sich darunter vorstellen?
Lösung zeigen
m/s²
Anstelle des Quadrates kann man auch (m/s)/s schreiben, also m/s pro Sekunde. Eine Beschleunigung von 3 m/s² bedeutet also, dass sich die Geschwindigkeit pro Sekunde um 3 m/s erhöht. einklappen
Welchen Wert hat die Erdbeschleunigung $g$? Nenne auch die Einheit!
Extremwertaufgaben
Wie sieht die allgemeine Vorgehensweise beim Lösen von Extremwertaufgaben aus?
Lösung zeigen
-
Die Zielfunktion wird erstellt. Das ist jene Funktion, die maximiert bzw. minimiert werden soll.
-
Falls die Zielfunktion mehr als eine Variable enthält, muss sie mittels Nebenbedingungen auf eine Variable reduziert werden.
-
Es werden die Extrempunkte der Zielfunktion berechnet und entsprechend der Aufgabenstellung der richtige Punkt gewählt.
einklappen
Möglichkeiten zur Unterstützung
© 2016 – 2024 MATHE.ZONE
|
