Fragen
Wie wird die Summe der ersten $n$ Glieder einer arithmetischen Folge berechnet?
Lösung zeigen
$s_n= n\cdot \frac{a_1+a_n}{2}$
Verbale Beschreibung: Es wird die Anzahl der Glieder mit dem Mittelwert aus erstem und letztem Glied multipliziert. einklappen
Wie kann die Summenformel für die ersten $n$ Glieder einer arithmetischen Folge hergeleitet werden?
Lösung zeigen
In dieser Herleitung werden zwei Fälle unterschieden.
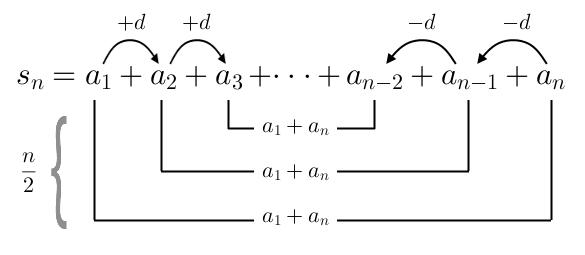
1. Fall: Ist die Anzahl $n$ der Glieder gerade, so kann die Summenformel anhand folgender Grafik erklärt werden:
Werden die Paare gemäß dieser Abbildung gebildet, so beträgt deren Wert immer $a_1+a_n$. Für die inneren Paare gilt dies, da der linke Summand um $d$ vergrößert wird, der rechte Summand jedoch um $d$ verkleinert wird. Somit heben sich diese Änderungen auf. Es bleibt daher immer beim Wert $a_1+a_n$. Insgesamt gibt es $\frac{n}{2}$ dieser Paare. Deren Summe wird berechnet, indem man den Wert mit der Anzahl multipliziert, also $\frac{n}{2}\cdot (a_1+a_n)$.
2. Fall: Ist die Anzahl der Glieder ungerade, so bleibt in der Mitte ein Glied übrig. Man hat daher nur $\frac{n-1}{2}$ Paare mit einem Wert von jeweils $a_1+a_n$. Das mittlere Glied besitzt den Wert $\frac{a_1+a_n}{2}$, also den arithmetischen Mittelwert der beiden äußersten Glieder. Für die Summe aller Glieder erhält man somit:
$$ \frac{n-1}{2} \cdot (a_1+a_n) + \frac{a_1+a_n}{2}$$
Durch Aufspalten des ersten Bruches erhält man folgenden Term:
$$ \frac{n}{2} \cdot (a_1+a_n)- \frac{1}{2} \cdot (a_1+a_n) + \frac{a_1+a_n}{2} = \frac{n}{2} \cdot (a_1+a_n)$$
Da sich der zweite und der dritte Summand aufheben, bleibt auch in diesem Fall die bereits bekannte Summenformel übrig. einklappen
Fehler melden