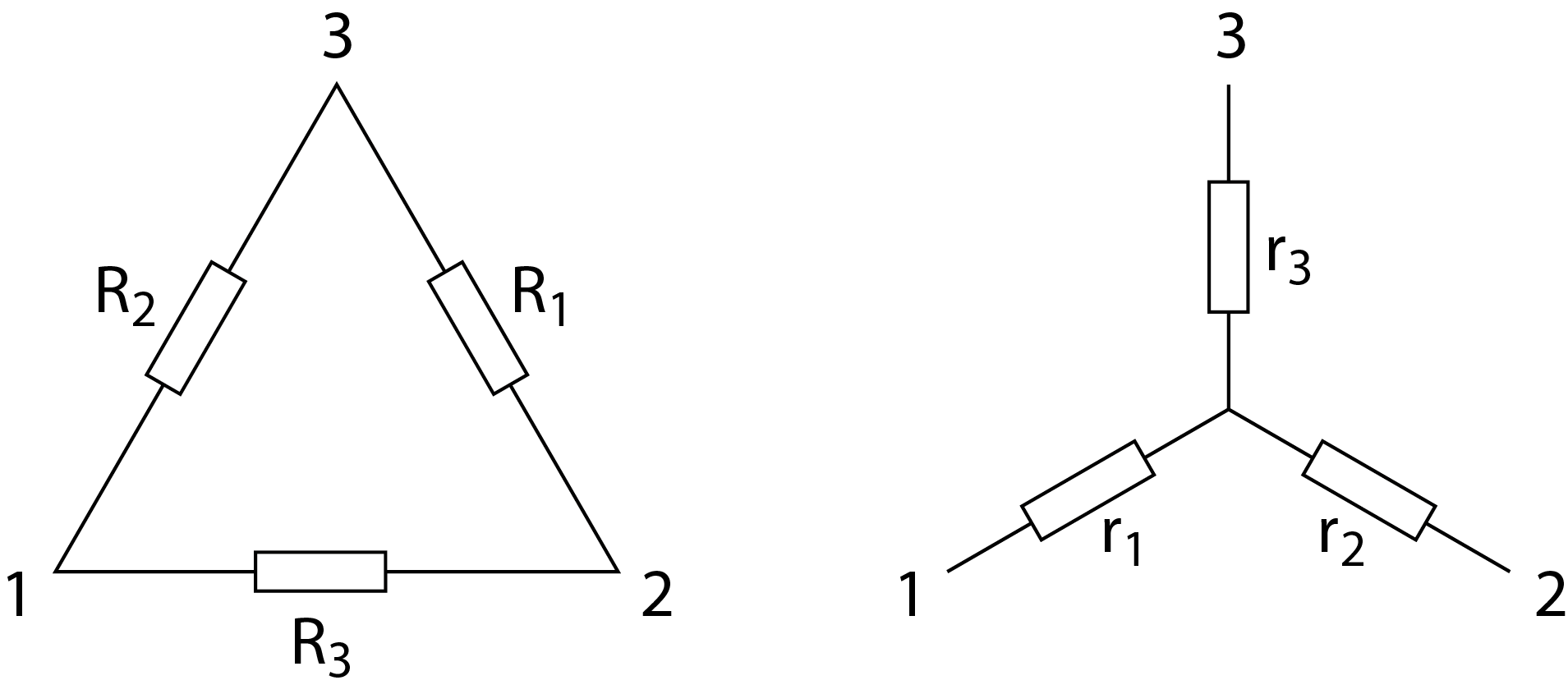
Dafür gelten die folgenden Zusammenhänge:
$$r_1+r_2=\frac{R_3\cdot (R_1+R_2)}{R_1+R_2+R_3}\hspace{1cm}r_2+r_3=\frac{R_1\cdot (R_2+R_3)}{R_1+R_2+R_3}\hspace{1cm}r_1+r_3=\frac{R_2\cdot (R_1+R_3)}{R_1+R_2+R_3}$$
Berechne die Widerstände $r_1,r_2,r_3$ der sternförmigen Schaltung, wenn die Widerstände der Dreiecksschaltung folgende sind: $R_1=24\,\Omega$, $R_2=35\,\Omega$, $R_3=59\,\Omega$.
$r_1=$ [2] $\Omega$
$r_2=$ [2] $\Omega$
$r_3=$ [2] $\Omega$