Aufgaben zur Trigonometrie im rechtwinkligen Dreieck
Auf dieser Seite befinden sich Aufgaben zur Trigonometrie im rechtwinkligen Dreieck. Jede Aufgabe besitzt eine Nummer, über welche sie durch die Suchfunktion jederzeit wieder aufgerufen werden kann. Dazu muss als Suchbegriff die Aufgabennummer mit einer Raute davor eingegeben werden, also z. B. #123. Die Aufgaben dieser Internetseite werden in jeder Session – also nach jedem Neustart des Webbrowsers oder nach jedem neuen Login – neu generiert. Bei den meisten Aufgaben bedeutet dies, dass sich einzelne Zahlenwerte verändern. Möchte man zu einem späteren Zeitpunkt erneut auf exakt dieselbe Aufgabe zugreifen, so sollte daher ein Screenshot angefertigt werden.
Inhaltsverzeichnis
1. Winkelfunktionen
Eine Kraft von 767 N wirkt in einem Winkel von 35° (gemessen zur Horizontalen). Berechne die horizontale und die vertikale Komponente dieser Kraft.
Bei einem Sturm wurde ein Baum in einer bestimmten Höhe abgeknickt. Die Spitze des Baumes berührt den Boden horizontal gemessen 8.8 m entfernt vom Baumstamm. Der Winkel zwischen dem abgeknickten Teil des Baumstamms und dem Boden beträgt 31°. Berechne, wie hoch der Baum war.
Der Steigungswinkel einer Rollstuhlrampe ist auf 4.3° festgelegt. Die Höhe der Rampe soll 80 cm betragen. Welche horizontale Länge muss die Rampe haben?
Auf einem Spielplatz soll eine gerade Rutsche errichtet werden, welche eine Höhe von 5 m aufweist. Aus Sicherheitsgründen soll der Winkel zur Horizontalen nur 22° betragen. Berechne die Länge des für die Rutsche notwendigen Materials.
Ein Gebäude wirft einen 55.5 m langen Schatten (beginnend bei der höchsten Stelle des Gebäudes). Die Sonnenstrahlen haben einen Einfallswinkel von 41.7° (gemessen zur Horizontalen). Berechne die Höhe des Gebäudes.
Eine Leiter wird an eine Wand gelehnt, sodass sie mit dem Boden einen Winkel von 78° einschließt. Sie ist am Boden 1.01 m von der Wand entfernt. Wie lang ist die Leiter und in welcher Höhe berührt sie die Wand?
Die Schnur eines Papierdrachens schließt mit dem ebenen Boden einen Winkel von 71° ein und ist 62 m lang. In welcher Höhe fliegt der Drache?
2. Umkehrfunktionen
Beim Parasailing soll sich die Person aus Sicherheitsgründen höchstens 10 m über dem Wasser befinden. Was ist der maximale Steigungswinkel der Leine, wenn diese eine Länge von 55 m hat?
Gegeben ist ein Rechteck mit den Seitenlängen 15 cm und 29 cm. Berechne den spitzen Winkel, den die beiden Diagonalen einschließen.
Mit einer horizontal gemessen 5.8 m langen Rollstuhlrampe wird eine Höhendifferenz von 45 cm überwunden. Berechne den Steigungswinkel der Rampe.
Ein gerader Straßenabschnitt ist laut einer Landkarte horizontal gemessen 760 m lang. Der Endpunkt liegt um 30 m höher als der Anfangspunkt. Berechne den Steigungswinkel des Straßenabschnitts.
3. Geometrische Figuren
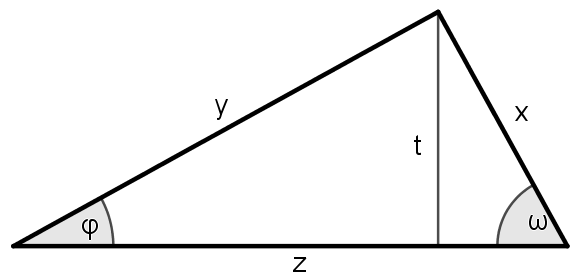
Vom nachfolgend abgebildeten rechtwinkligen Dreieck sind die Abmessungen $x=40$ cm und $z=9.4$ dm bekannt. Berechne den Flächeninhalt $A$, den Winkel $\omega$ und die Höhe $t$. Achte auf die Einheiten! Die Skizze ist nicht maßstabsgetreu.
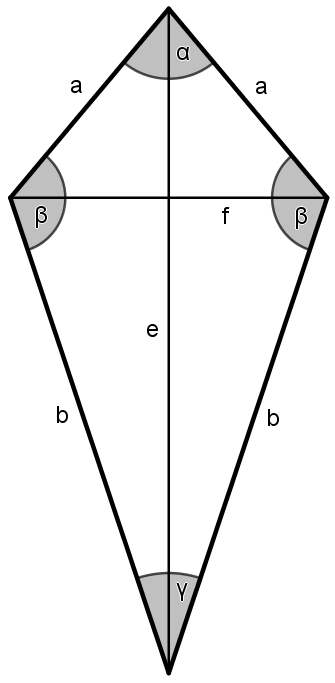
Von einem Deltoid sind die beiden Seitenlängen $a=38$ mm und $b=82$ mm sowie der Winkel $\gamma=36\,^\circ$ bekannt. Berechne die gesuchten Größen. Achte auf die Einheiten! Die Skizze ist nicht maßstabsgetreu.
#578 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Gegeben ist ein rechtwinkliges Dreieck mit dem Winkel α = 46° und dem Flächeninhalt A = 64 cm². Berechne die Länge der drei Seiten.
Gegeben ist die unten abgebildete geometrische Figur (nicht maßstabsgetreu). Man kennt die Seitenlängen $c = 64\, \mathrm{cm}$ und $d = 95 \,\mathrm{cm}$ sowie den Winkel $\alpha = 80 °$.
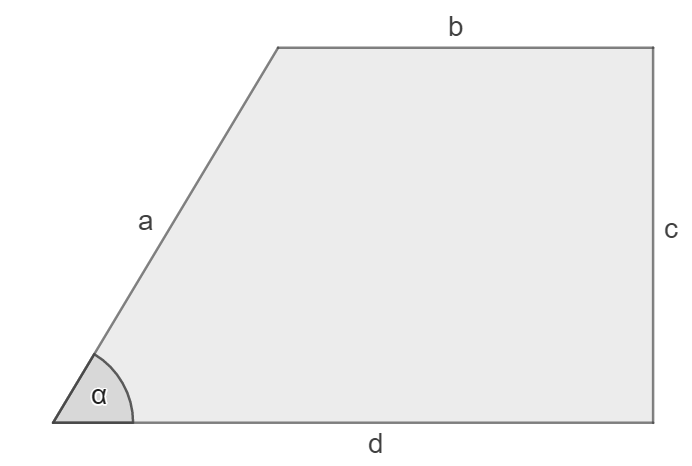
a) Bestimme den Umfang der Figur!
b) Bestimme den Flächeninhalt der Figur!
#1048 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
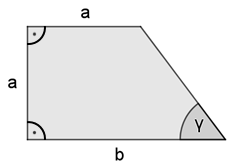
Stelle jeweils eine Formel auf, mit welcher der Flächeninhalt und der Umfang der abgebildeten Figur berechnet werden können. Verwende dazu ausschließlich die Variablen $a$, $b$ und $\gamma$. Vereinfache die Formeln möglichst weit.
4. Steigungswinkel und Steigung
#363 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Die sogenannte „Streif“ (die Abfahrtspiste in Kitzbühel) hat eine horizontale Streckenlänge von 3312 m. Der Start befindet sich in einer Höhe von 1665 m und das Ziel in einer Höhe von 805 m.
a) Berechne das durchschnittliche Gefälle in Prozent.
b) Berechne den durchschnittlichen Steigungswinkel.
c) An der steilsten Stelle, der sogenannten Mausefalle, beträgt das Gefälle 85 %. Welchem Winkel entspricht das?
Eine Bahnstrecke hat eine Steigung von 1/396.
a) Gib diese Steigung in Prozent an und berechne den zugehörigen Steigungswinkel.
b) Welcher Höhenunterschied wird auf einer horizontalen Entfernung von 3.2 km überwunden?
#1017 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Das Verkehrszeichen „Starke Steigung“ sieht folgendermaßen aus:
a) Gib an, welchem Steigungswinkel eine Steigung von 10 % entspricht!
b) Die im Verkehrsschild abgebildete Steigung ist deutlich größer als 10 %. Berechne bzw. argumentiere (abmessen alleine ist nicht ausreichend), wie groß der abgebildete Steigungswinkel tatsächlich ist. Das Verkehrszeichen entspricht einem gleichseitigen Dreieck und die schwarze und die weiße Fläche sind gleich groß.
#1063 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Argumentiere, ob die folgende Aussage richtig oder falsch ist: „Eine Steigung von 100 % entspricht einem Steigungswinkel von 90 Grad.“
5. Vermessungsaufgaben
Ein Turm wirft auf einem ebenen Feld einen 23.4 m langen Schatten. Die Sonnenhöhe beträgt 49°. Wie hoch ist der Turm?
Philipp befindet sich 183 m von einem Turm entfernt (horizontal gemessen). Er steht auf einem kleinen Hügel und sieht von dort aus die Turmspitze unter einem Höhenwinkel von 8.1° und den Fußpunkt des Turms unter einem Tiefenwinkel von 2.1°.
a) Erstelle eine vollständig beschriftete Skizze.
b) Berechne die Höhe des Turms.
Vom Dach eines 34 m hohen Turms sieht man die Ufer eines Flusses unter den Tiefenwinkeln 16.2° und 12.7°.
a) Zeichne eine aussagekräftige Skizze dieses Sachverhalts inklusive aller Beschriftungen!
b) Wie weit ist der Turm vom näheren Flussufer entfernt?
c) Wie breit ist der Fluss?
Von der 150 m hoch gelegenen Aussichtsplattform des Wiener Donauturms sieht Marie ihr Wohnhaus unter einem Tiefenwinkel von 3° 23'. Berechne unter Vernachlässigung der Krümmung der Erdoberfläche, wie weit entfernt sie vom Donauturm wohnt.
Es soll die Höhe eines Turmes bestimmt werden. Dazu misst man den Winkel, unter welchem man vom Boden aus die Turmspitze sieht, von zwei Punkten A und B. Vom näher am Turm liegenden Punkt A wird ein Höhenwinkel von 4.4° gemessen. Der um 135 m weiter entfernt liegende Punkt B ergibt einen Winkel von 3.4°.
a) Zeichne eine vollständig beschriftete Skizze des Sachverhalts.
b) Berechne die Höhe $h$ des Turms.
6. Aufgaben aus Technik und Physik
Ein PKW mit der Gewichtskraft $F_G=1.5\,\mathrm{kN}$ fährt eine Straße mit einer Steigung von 15 % hinauf. Dabei zieht ihn die Hangabtriebskraft $F_T$ parallel zur Straße nach unten und die Normalkraft $F_N$ drückt ihn im rechten Winkel gegen die Straße.
a) Berechne den Steigungswinkel.
b) Zeichne eine aussagekräftige Skizze des Sachverhalts. Trage alle Kräfte sowie den bekannten Winkel ein.
c) Wie groß ist die Hangabtriebskraft, welche ihn parallel zur Straße nach unten zieht?
d) Wie groß ist die Normalkraft, welche ihn gegen die Straße drückt?
Zwei Kräfte $F_1= 3.41\,\textrm{kN}$ und $F_2 = 5.4\,\textrm{kN}$ stehen normal (im rechten Winkel) aufeinander.
a) Berechne die resultierende Kraft $F_R$.
b) Berechne den Winkel zwischen $F_1$ und $F_R$.
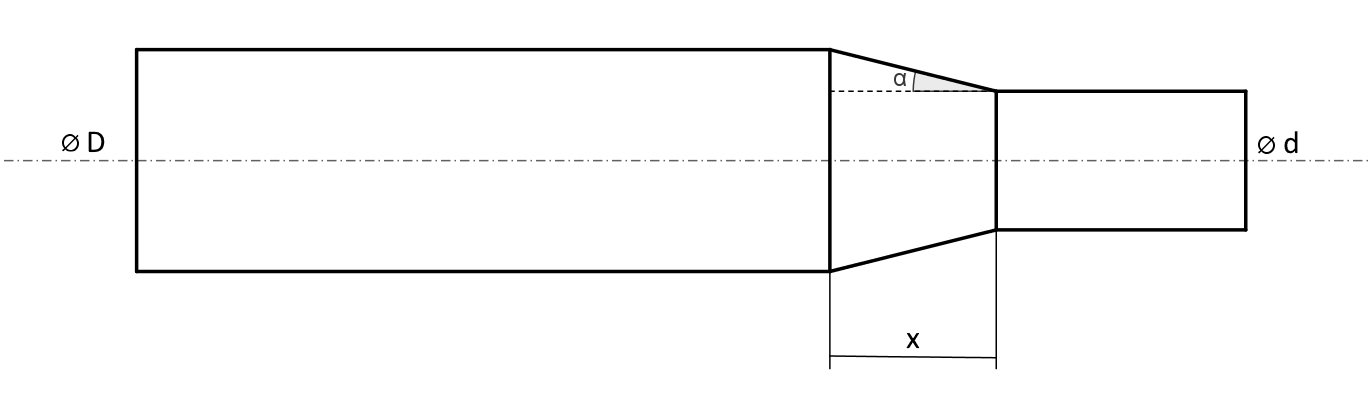
Berechne den Winkel $\alpha$ des nachfolgend abgebildeten rotationssymmetrischen Bauteils! Folgende Werte sind bekannt: $D=20\,\textrm{mm}$, $d=14\,\textrm{mm}$ und $x=14\,\textrm{mm}$. Die Skizze ist nicht maßstabsgetreu.
7. Vermischte Aufgaben
#626 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
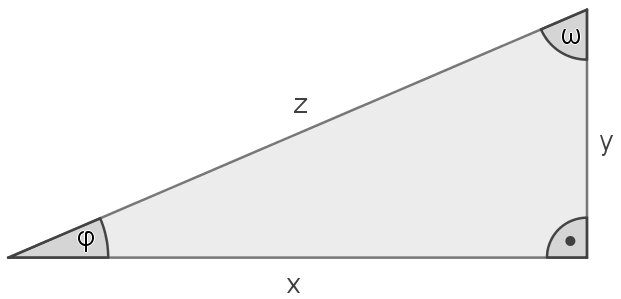
Ergänze anhand der unten abgebildeten Skizze die folgenden Winkelfunktionen und Umkehrfunktionen. Die Namen der Winkel lauten „phi“ ($\varphi$) und „omega“ ($\omega$).
$\sin(\varphi)=$
$\tan(\omega)=$
$\cos(\omega)=$
$\arctan\left(\tfrac{y}{x}\right)=$
$\arccos\left(\tfrac{x}{z}\right)=$
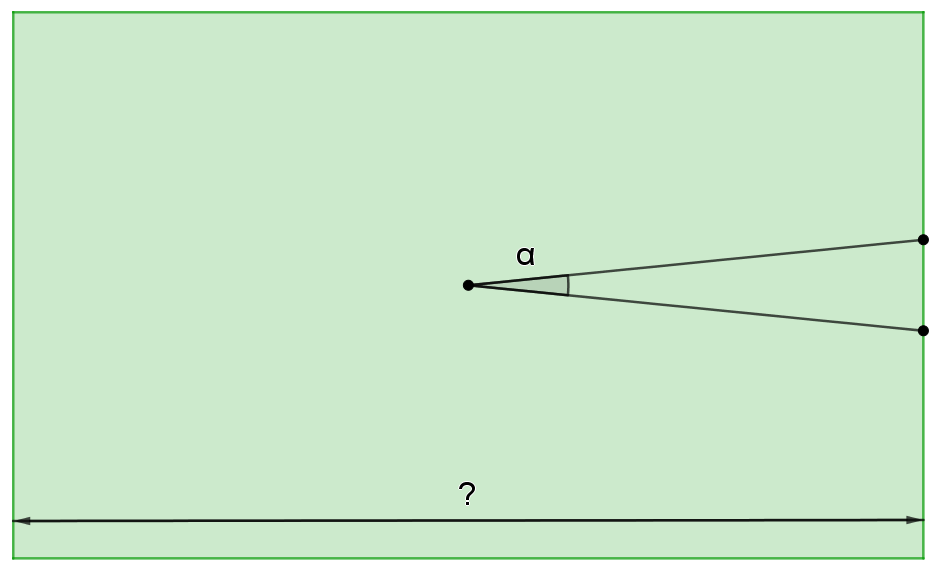
Steht man im Mittelpunkt eines Fußballfeldes, so sieht man zwischen den beiden Pfosten eines Tores einen Winkel von $\alpha=8^\circ\,11'$ (siehe Skizze). Die Breite eines Fußballtores beträgt bekanntlich 7,32 m. Wie lang ist dieses Fußballfeld?
#1064 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Gib an, ob die folgenden Aussagen wahr oder falsch sind.
Für die beiden spitzen Winkel eines rechtwinkligen Dreiecks gilt allgemein $\sin(\alpha) = \cos(\beta)$.
Für die beiden spitzen Winkel eines rechtwinkligen Dreiecks gilt allgemein $\tan(\alpha) = \tan(\beta)$.
Für die beiden spitzen Winkel eines rechtwinkligen Dreiecks gilt allgemein $\tan(\alpha) \cdot \tan(\beta) = 1$.
Es gilt allgemein $\tan(\alpha) = \frac{\cos(\alpha)}{\sin(\alpha)} $.
Es gilt allgemein $\tan(\alpha) = \frac{\sin(\alpha)}{\cos(\alpha)} $.#1213 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Von der Erde aus betrachtet erscheint die Sonne unter einem Winkel von 32'. Die mittlere Entfernung zwischen Erde und Sonne beträgt 149,6 Mio. km. Berechne anhand dieser Daten den Durchmesser der Sonne.
#1305 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
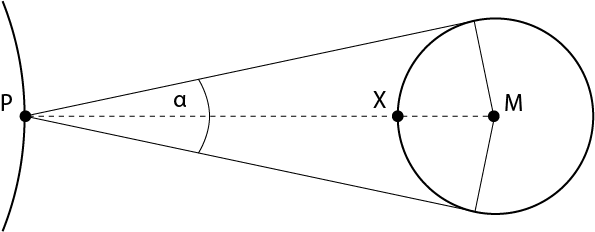
Zu einem bestimmten Zeitpunkt konnte der Mond von der Erde aus unter einem Sehwinkel von 30' 27'' betrachtet werden. Sein Durchmesser beträgt 3474 km. Wie weit war der nächste Punkte des Mondes (also Punkt $X$ der folgenden Abbildung) zu dieser Zeit von der Erde entfernt?
#1319 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Von einem Parallelogramm sind die Seitenlänge $b=19\,\mathrm{mm}$, die Diagonale $e=48\,\mathrm{mm}$ und der Winkel $\beta=128^\circ$ bekannt.
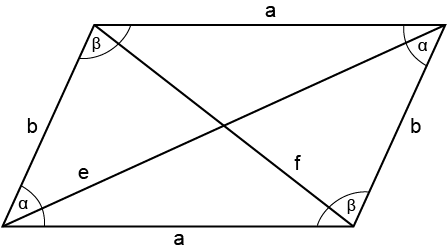
a) Berechne den Winkel $\alpha$.
b) Berechne die Höhe $h_a$.
c) Berechne die Seitenlänge $a$.
d) Berechne die Diagonale $f$.
e) Berechne den Flächeninhalt $A$ in cm².
#1349 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Wie weit über der Erdoberfläche muss sich ein Astronaut befinden, damit er die Erde unter einem Sehwinkel von 8.8° sieht? Der Erdradius beträgt 6371 km.
#1375 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Von einem rechtwinkligen Dreieck ist bekannt, dass der Flächeninhalt 38.7 cm² beträgt und der Winkel $\beta$ den Wert 61° hat. Berechne die drei Seitenlängen.
#1376 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Der Umfang eines gleichschenkligen Dreiecks beträgt 26.5 cm. Die Basis $c$ ist 6.5 cm lang. Berechne die Länge der Schenkel, den Flächeninhalt und alle Winkel.
| Urheberrechtshinweis: Die auf dieser Seite aufgelisteten Aufgaben unterliegen dem Urheberrecht (siehe Impressum). |