Aufgaben zur Trigonometrie im allgemeinen Dreieck
Auf dieser Seite befinden sich Aufgaben zur Trigonometrie im allgemeinen Dreieck. Jede Aufgabe besitzt eine Nummer, über welche sie durch die Suchfunktion jederzeit wieder aufgerufen werden kann. Dazu muss als Suchbegriff die Aufgabennummer mit einer Raute davor eingegeben werden, also z. B. #123. Die Aufgaben dieser Internetseite werden in jeder Session – also nach jedem Neustart des Webbrowsers oder nach jedem neuen Login – neu generiert. Bei den meisten Aufgaben bedeutet dies, dass sich einzelne Zahlenwerte verändern. Möchte man zu einem späteren Zeitpunkt erneut auf exakt dieselbe Aufgabe zugreifen, so sollte daher ein Screenshot angefertigt werden.
Inhaltsverzeichnis
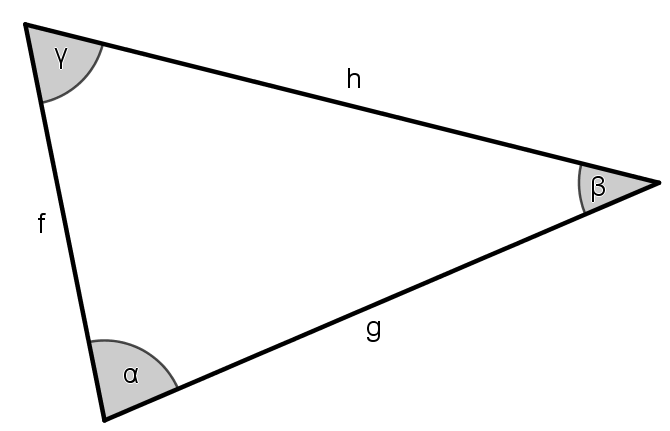
Von einem Dreieck kennt man folgende Daten: $f=931$ m, $h=1.75$ km und $\gamma=70.4\,^\circ$. Berechne die fehlenden Größen und achte dabei auf die Einheiten! Die Skizze ist nicht maßstabsgetreu.
Valentin und Isabella stehen auf einer Aussichtsplattform und sehen von dort aus zwischen ihren Wohnhäusern einen Winkel von 43°. Valentin wohnt 3.7 km von dieser Aussichtsplattform entfernt. Isabella wohnt in einer Entfernung von 4.7 km. Berechne die direkte Entfernung der Wohnhäuser von Valentin und Isabella. Vernachlässige dabei die Krümmung der Erde.
In der nachfolgenden Abbildung ist ein viereckiges Grundstück zu sehen. Von diesem Grundstück kennt man die Seitenlängen $a=25\,\mathrm{m}$, $b=50\,\mathrm{m}$, $c=35\,\mathrm{m}$ und $d=40\,\mathrm{m}$, sowie den Winkel $\alpha = 120°$. Die Abbildung ist nicht maßstabsgetreu.
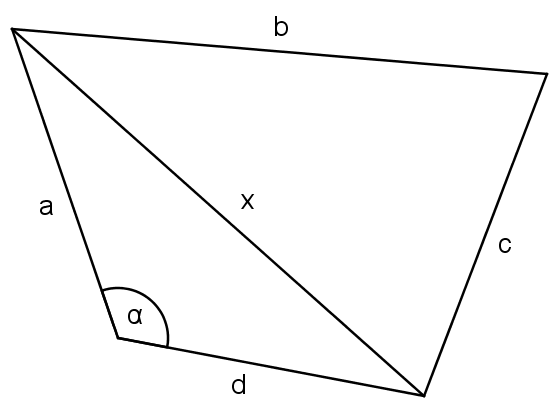
a) Berechne die Länge der Diagonale $x$.
b) Berechne den Flächeninhalt des gesamten Grundstücks.
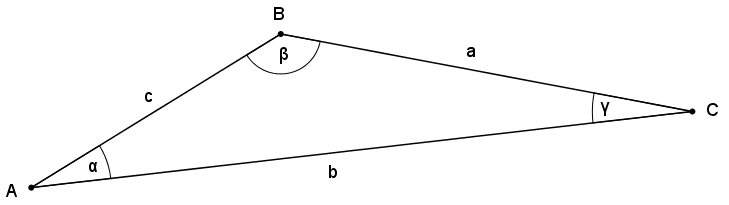
Vom abgebildeten Dreieck kennt man $b=90\,\mathrm{cm}$, $c=50\,\mathrm{cm}$ und $\gamma =20°$. Berechne den Winkel $\beta$.
Zwei Sterne haben zur Erde eine Entfernung von 17.2 ly und 26.8 ly. Dabei ist ly die internationale Abkürzung der Längeneinheit Lichtjahr (ca. $9{,}461\cdot 10^{15}$ m). Am Nachthimmel wird zwischen den beiden Sternen ein Winkel von 46.4° gemessen. Berechne den Abstand der beiden Sterne.
Es soll die Höhe eines Turmes bestimmt werden. Dazu misst man den Winkel, unter welchem man vom Boden aus die Turmspitze sieht, von zwei Punkten A und B. Vom näher am Turm liegenden Punkt A wird ein Höhenwinkel von 4.3° gemessen. Der um 149 m weiter entfernt liegende Punkt B ergibt einen Winkel von 3.2°.
a) Zeichne eine vollständig beschriftete Skizze des Sachverhalts.
b) Berechne die Höhe $h$ des Turms.
Ein Winkel eines allgemeinen Dreiecks beträgt 46° und die beiden anliegenden Seiten sind 64 mm und 28 mm lang.
a) Erstelle eine Skizze, in welcher alle bekannten Größen und alle verwendeten Variablen ersichtlich sind.
b) Bestimme den Flächeninhalt.
c) Berechne alle fehlenden Winkel und Seitenlängen.
Zwei Schiffe A und B verlassen gleichzeitig denselben Hafen und bewegen sich im betrachteten Zeitraum auf geraden Wegen. Zwischen ihren Routen liegt ein Winkel von 81°. Schiff A bewegt sich mit einer konstanten Geschwindigkeit von 16.7 Knoten und Schiff B mit einer konstanten Geschwindigkeit von 11.9 Knoten. Ein Knoten entspricht einer Geschwindigkeit von 1,852 km/h.
a) Erstelle eine aussagekräftige Skizze des Sachverhalts.
b) Rechne die Geschwindigkeiten der beiden Schiffe in km/h um.
c) Berechne, wie weit die beiden Schiffe 40 Minuten nach Verlassen des Hafens voneinander entfernt sind.
#1379 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Nachfolgend ist ein Dreieck abgebildet.
a) Erstelle eine Formel, mit welcher die Seitenlänge $h$ unter Verwendung des Sinussatzes berechnet werden kann.
b) Erstelle eine Formel, mit welcher der Winkel $\gamma$ unter Verwendung des Kosinussatzes berechnet werden kann.
c) Erstelle eine Formel, mit welcher die Seitenlänge $g$ unter Verwendung des Kosinussatzes berechnet werden kann.
#1380 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Von einem Dreieck sind der Winkel $\alpha = 35^\circ$, die Länge der gegenüber von $\alpha$ liegende Seiten $a=34\,\mathrm{mm}$ und die Länge der Seite $b=52\,\mathrm{mm}$ bekannt.
a) Erkläre durch eine Skizze und eine dazu passende Beschreibung, warum diese Angabe nicht eindeutig ist.
b) Es soll jene Variante ausgewählt werden, bei welcher der Winkel $\beta$ stumpf ist. Berechne alle fehlenden Winkel und Seitenlängen, sowie den Flächeninhalt (in der Einheit cm²).