Aufgaben zur Rentenrechnung
Auf dieser Seite befinden sich Aufgaben zur Rentenrechnung. Jede Aufgabe besitzt eine Nummer, über welche sie durch die Suchfunktion jederzeit wieder aufgerufen werden kann. Dazu muss als Suchbegriff die Aufgabennummer mit einer Raute davor eingegeben werden, also z. B. #123. Die Aufgaben dieser Internetseite werden in jeder Session – also nach jedem Neustart des Webbrowsers oder nach jedem neuen Login – neu generiert. Bei den meisten Aufgaben bedeutet dies, dass sich einzelne Zahlenwerte verändern. Möchte man zu einem späteren Zeitpunkt erneut auf exakt dieselbe Aufgabe zugreifen, so sollte daher ein Screenshot angefertigt werden.
Inhaltsverzeichnis
1. Barwert, Endwert oder Ratenhöhe berechnen
Jemand nimmt einen Kredit in Höhe von 22.000 € auf. Als Zinssatz werden 8.6 % p.a. vereinbart. Die Schuld soll durch 11 gleich hohe Jahresraten beglichen werden, wobei die erste Ratenzahlung ein Jahr nach der Kreditaufnahme erfolgt. Berechne die Höhe der Raten.
#1452 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Frau Hummer ging am 01.01.2023 in Pension. Durch eine private Pensionsversicherung hat sie 45000 € angespart, welche innerhalb der nächsten 15 Jahre durch jeweils gleich große Beträge $R$ vollständig ausgezahlt werden sollen. Der Zinssatz beträgt 2.5 % p.a. und die Zahlungen erfolgen jeweils am Jahresanfang. Berechne $R$.
2. Ratenanzahl berechnen
#520 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Erstelle aus der nachfolgenden Formel für den Endwert einer nachschüssigen Jahresrente eine Formel zur Berechnung der Jahre $n$.
$$E_{\mathrm{nach}}=R\cdot \frac{q^n-1}{q-1}$$
Eine Schuld von 4000 € soll durch monatliche Raten von 180 € zurückgezahlt werden. Der vereinbarte Monatszinssatz beträgt 0.55 %. Die erste Zahlung erfolgt in genau einem Monat.
a) Berechne die Anzahl der Vollraten.
b) Berechne den Restbetrag, der gleichzeitig mit der letzten Vollrate bezahlt wird.
3. Zinssatz berechnen
Jemand kauft heute einen neuen Computer um 1399 €. Es besteht die Möglichkeit, diesen Betrag durch 12 nachschüssige Monatsraten zu je 121.9 € zu bezahlen. Berechne den effektiven Jahreszinssatz dieser Rente!
Ein heute aufgenommener Kredit in Höhe von 30000 € soll durch eine nachschüssige Jahresrente mit 10 Raten zu je 3487 € zurückgezahlt werden. Berechne den Zinssatz dieser Rente.
4. Tilgungspläne
Es ist nachfolgend ein Teil eines Tilgungsplanes gegeben.
a) Berechne den Jahreszinssatz.
b) Vervollständige die zweite und die dritte Zeile des Tilgungsplans.
| Jahr | Zinsanteil | Tilgungsanteil | Annuität | Restschuld |
|---|---|---|---|---|
| 0 | — | — | — | 5100 € |
| 1 | 219 € | 1223 € | ||
| 2 | 1223 € |
5. Vermischte Aufgaben
Jemand zahlt 34 Jahre lang jedes Monatsende 38 € auf ein privates Pensionskonto. Der Zinssatz beträgt 1.35 % p.a. Anschließend wird das Angesparte über einen Zeitraum von 11 Jahren in gleichen monatlichen Raten ausbezahlt. Die erste Auszahlung erfolgt ein Monat nach der letzten Einzahlung.
a) Berechne den äquivalenten Monatszinssatz!
b) Berechne, welcher Betrag sich unmittelbar nach der letzten Einzahlung am Pensionskonto befindet.
c) Berechne die Höhe der monatlichen Auszahlungen.
Jemand legt zum Zeitpunkt $t=0$ einen Betrag von 25.000 € für die Dauer von 10 Jahren auf ein mit 3 % p.a. verzinstes Konto. Anschließend möchte sich die Person den am Konto vorhandenen Betrag über 20 Jahre hinweg durch gleich große jährliche Zahlungen auszahlen lassen, wobei die erste Zahlung sofort nach Ablauf der 10 Jahre, also zum Zeitpunkt $t=10$, erfolgt. Bis zur letzten Zahlung wird das Konto durchgehend mit 3 % p.a. verzinst. Nach der letzten Zahlung ist das Konto leer.
a) Veranschauliche alle Ein- und Auszahlungen auf der folgenden Zeitachse.
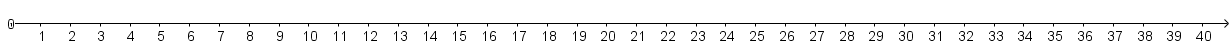
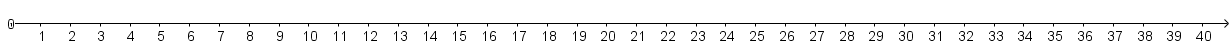
b) Berechne, welchen Betrag die Person jährlich ausgezahlt bekommt.
#701 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Ordne den vier Beschreibungen den richtigen Term zu (einer bleibt übrig). Wähle dazu den richtigen Buchstaben aus. Der Zinssatz beträgt für die gesamte Aufgabe $i=5\,\%$ und die Ratenhöhe ist jeweils 200 €.
Barwert einer vorschüssigen Semesterrente mit einer Laufzeit von 5 Jahren:
Endwert einer nachschüssigen Jahresrente mit einer Laufzeit von 10 Jahren:
Barwert einer nachschüssigen Monatsrente mit insgesamt 10 Raten:
Endwert einer vorschüssigen Semesterrente mit insgesamt 10 Raten:
$$(\mathrm{A})~~ 200\cdot \frac{\sqrt{1{,}05}^{10}-1}{\sqrt{1{,}05}-1}\cdot \sqrt{1{,}05}~~~~~~~~~~~~~~~~~~~(\mathrm{B})~~ 200\cdot \frac{1{,}05^{10}-1}{1{,}05-1}~~~~~~~~~~~~~~~~~(\mathrm{C})~~ 200\cdot \frac{\sqrt[12]{1{,}05}^{10}-1}{\sqrt[12]{1{,}05}-1}$$
$$(\mathrm{D})~~ 200\cdot \frac{\sqrt{1{,}05}^{10}-1}{\sqrt{1{,}05}-1}\cdot \frac{1}{\sqrt{1{,}05}^9}~~~~~~~~~~~~~~~~~~~~~~(\mathrm{E})~~ 200\cdot \frac{1-\sqrt[12]{1{,}05}^{-10}}{\sqrt[12]{1{,}05}-1}$$#1151 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
In unterschiedlichen Büchern findet man häufig unterschiedliche Formeln für ein und dieselbe Sache. Beispielsweise gibt es für die Berechnung des Barwerts einer vorschüssigen Rente folgende Formeln:
$$B_1=R\cdot \frac{q^n-1}{q-1}\cdot \frac{1}{q^{n-1}} \hspace{3cm} B_2=R\cdot \frac{q^n-1}{q-1}\cdot q^{1-n} \hspace{3cm} B_3=R \cdot \frac{1-q^{-n}}{q-1}\cdot q$$
Zeige durch mathematische Umformungen und dazu passende Erklärungen, dass diese drei Formeln tatsächlich gleichwertig sind.
Möglichkeiten zur Unterstützung
© 2016 – 2024 MATHE.ZONE