Aufgaben zu quadratischen Funktionen
Auf dieser Seite befinden sich Aufgaben zu quadratischen Funktionen. Jede Aufgabe besitzt eine Nummer, über welche sie durch die Suchfunktion jederzeit wieder aufgerufen werden kann. Dazu muss als Suchbegriff die Aufgabennummer mit einer Raute davor eingegeben werden, also z. B. #123. Die Aufgaben dieser Internetseite werden in jeder Session – also nach jedem Neustart des Webbrowsers oder nach jedem neuen Login – neu generiert. Bei den meisten Aufgaben bedeutet dies, dass sich einzelne Zahlenwerte verändern. Möchte man zu einem späteren Zeitpunkt erneut auf exakt dieselbe Aufgabe zugreifen, so sollte daher ein Screenshot angefertigt werden.
Inhaltsverzeichnis
1. Nullstellen und Schnittpunkte
Berechne die Nullstellen der quadratischen Funktion $f(x)=2.89\cdot (x+6.71)^2-12.4$. Zur Eindeutigkeit des Ergebnisses soll $x_1$ die kleinere der beiden Nullstellen sein.
Berechne die Schnittstellen der quadratischen Funktionen $f(x)=1.46x^2+3.53x-1.94$ und $g(x)=-1.28x^2+1.71x+2.28$. Zur Eindeutigkeit des Ergebnisses soll $x_1$ die kleinere der beiden Schnittstellen sein.
Berechne die Schnittstellen der quadratischen Funktion $f(x)=1.27x^2+1.88x-1.63$ und der linearen Funktion $g(x)=-1.5x+2.62$.
Berechne, welchen Wert der Parameter $c$ haben muss, sodass die quadratische Funktion $f(x)=-3.49x^2+2.38x+c$ genau eine Nullstelle besitzt.
#507 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Ein Mathematiklehrer sucht für eine Aufgabe eine quadratische Funktion $f(x) = ax^2 + bx + c$, welche keine reelle Nullstelle besitzt. Wie kann er vorgehen, um passende Koeffizienten $a, b, c$ zu finden, wenn er nicht nur einfach solange zufällige Zahlen ausprobieren möchte, bis es passt?
#1099 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Begründe nachvollziehbar, ob die folgende Aussage richtig oder falsch ist: Sind $a,b,c>0$, dann hat die quadratische Funktion $f(x)=ax^2+bx+c$ immer zwei reelle Nullstellen.
2. Scheitelpunkt
#338 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Eine quadratische Funktion ist in Scheitelpunktform $f(x) = a \cdot (x -x_s)^2 + y_s$ gegeben. Gib eine mögliche Auswahl der Koeffizienten $a, x_s, y_s$ an, sodass die Funktion keine reelle Nullstelle hat. Beschreibe deine Vorgehensweise möglichst ausführlich und nachvollziehbar.
#1090 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Gib an, ob die folgenden Aussagen wahr oder falsch sind.
Die Parabel mit der Funktionsgleichung $f(x) = x^2 + 3$ hat den Scheitelpunkt bei $(\, 3 \mid 0 \,)$.
Die Parabel mit der Funktionsgleichung $f(x) = x^2 - 5$ hat den Scheitelpunkt bei $(\, 5 \mid 0 \,)$.
Die Parabel mit der Funktionsgleichung $f(x) = x^2 + 4$ hat den Scheitelpunkt bei $(\, 0 \mid 4 \,)$.
Die Parabel mit der Funktionsgleichung $f(x) = (x - 7)^2$ hat den Scheitelpunkt bei $(\, 7 \mid 0 \,)$.3. Funktionsgleichungen
Nachfolgend ist der Graph einer quadratischen Funktion abgebildet. Erstelle die zugehörige Funktionsgleichung in Polynomform $f(x)=ax^2+bx+c$. Es ist sinnvoll, diese zuerst in Scheitelpunktform zu erstellen und anschließend umzurechnen.
Von einer quadratischen Funktion ist bekannt, dass sie den Scheitelpunkt $(46.4 \mid 39.5)$ besitzt und zusätzlich durch den Punkt $(-20.7 \mid -21.8)$ verläuft. Bestimme die Koeffizienten $a,b,c$ der Polynomform $f(x)=ax^2+bx+c$ dieser quadratischen Funktion.
Eine quadratische Funktion verläuft durch die drei Punkte $(-4.6 \mid -1.3)$, $(2.2 \mid 5.8)$ und $(10.5 \mid -3.5)$. Erstelle die Funktionsgleichung dieser Funktion in der Form $f(x)=ax^2+bx+c$.
#658 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Ergänze die Lücken der Funktionsterme und achte dabei auf die vorgegebenen Vorzeichen.
a) Blauer Graph: $~f(x)=-0.2\cdot(x-\,\_\_\_\_\_\,)\cdot(x+\,\_\_\_\_\_\,)$
b) Roter Graph: $~g(x)=-0.2 \cdot(x-\,\_\_\_\_\_\,)^2+\,\_\_\_\_\_$
c) Grüner Graph: $~h(x)=0.5x^2-1.3x+\,\_\_\_\_\_$
#1141 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Es sind die drei Punkte $(\, -5 \mid 1 \,)$, $(\, -1 \mid 7 \,)$ und $(\, 7 \mid -1 \,)$ gegeben. Erstelle mittels GeoGebra die Funktionsgleichung einer quadratischen Funktion, deren Graph durch diese Punkte verläuft.
4. Funktionsgraph
Zeichne zur Funktionsgleichung $f(x)=ax^2+bx+c$ den Graphen einer beliebigen Funktion, welche die Eigenschaften $a>0$, $b=0$ und $c<0$ erfüllt und gib deren Funktionsgleichung an.
#714 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Erkläre, welches Vorzeichen die Parameter $a$ und $c$ haben müssen, damit der Graph von $f(x)=ax^2+c$ dem unten abgebildeten entspricht.
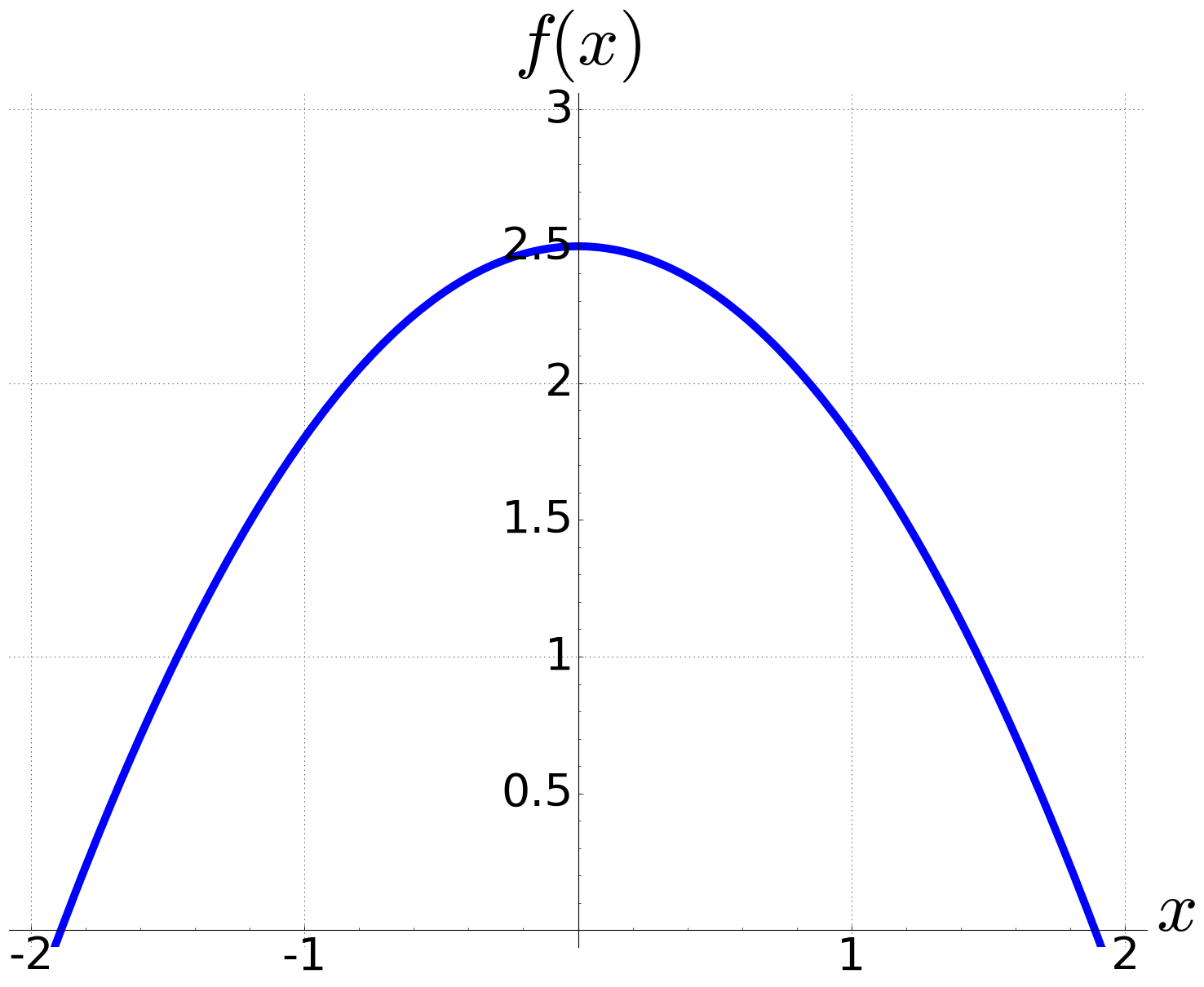
#973 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Nachfolgend sind vier quadratische Funktionen gegeben.
▪
$f(x)=ax^2+bx$ mit $a<0$ und $b>0\,\,\,\,\,$ ▪
$f(x)=ax^2+bx$ mit $a>0$ und $b<0\,\,\,\,\,$ ▪
$f(x)=ax^2+c$ mit $a<0$ und $c<0\,\,\,\,\,$ ▪
$f(x)=ax^2+c$ mit $a>0$ und $c>0\,\,\,\,\,$
Überprüfe jeweils, welche der unten genannten Eigenschaften auf die oben genannten Funktionen zutreffen.
▪
A ... Der Funktionsgraph verläuft durch den Ursprung des Koordinatensystems. ▪
B ... Der Funktionsgraph ist symmetrisch bezüglich der Ordinate (y-Achse). ▪
C ... Der Funktionsgraph ist nach oben offen. ▪
D ... Die Funktion besitzt keine reelle Nullstelle.5. Allgemeine Textaufgaben
#342 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Die nachfolgende Grafik zeigt eine parabelförmige Bogenbrücke. An den Punkten A und C ist der Brückenbogen im Gelände verankert und Punkt B ist der Scheitelpunkt des Brückenbogens. Die Straße verläuft entlang der horizontalen Achse. Alle Angaben sind in Meter.
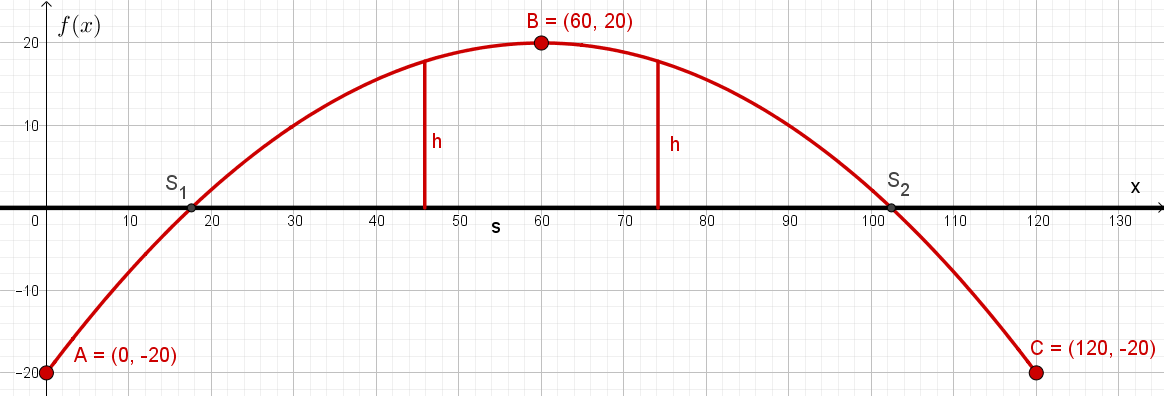
a) Ermittle eine Funktionsgleichung, welche die Form des Brückenbogens gemäß dieser Abbildung beschreibt.
b) Berechne die Spannweite $s$ der Brücke, also die Entfernung zwischen den beiden Schnittpunkten S1 und S2 des Brückenbogens und der Straße.
c) Berechne die Höhe $h$ der beiden Brückenpfeiler, welche jeweils nach einem Drittel der Spannweite errichtet werden sollen.
Die Flugkurve eines Speers entspricht einer Parabel (siehe Abbildung) und kann durch folgende quadratische Funktion beschrieben werden:
$$f(x)=-1.24\cdot 10^{-2}\cdot x^2+0.53\cdot x+2.16$$
Dabei werden $f(x)$ und $x$ jeweils in Metern gemessen.
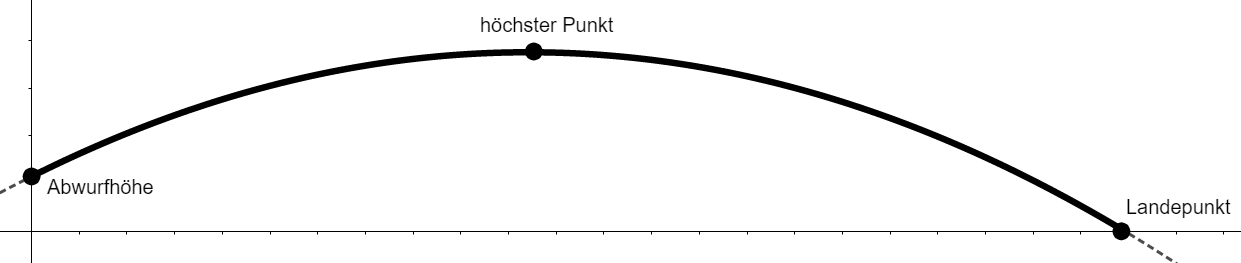
a) Ermittle die Abwurfhöhe des Speers.
b) Berechne, in welcher horizontalen Entfernung vom Abwurf der Speer gelandet ist.
c) Berechne die maximale Flughöhe des Speers.
6. Wirtschaftliche Anwendungen
Die Gewinnfunktion eines Produktes lautet $G(x)=-3x^2 + 265 x - 3878$.
a) Ermittle jenen Gewinn, der bei einer Produktionsmenge von 65 ME vorliegt.
b) Berechne, für welche Produktionsmengen der Gewinn 300 GE beträgt.
c) Ermittle den maximalen Gewinn, welcher mit diesem Produkt erzielt werden kann, und die dafür notwendige Produktionsmenge.
#999 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Nachfolgend sind die Funktionsgraphen der Kostenfunktion $K$ (rot) und der Erlösfunktion $E$ (blau) abgebildet. Bestimme die gesuchten Kennzahlen.
a) Verkaufspreis
b) Gewinnzone
c) Gewinn bei 40 ME
d) Fixkosten
#1293 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Es wurde untersucht, welche Kosten durch die Herstellung verschiedener Mengen entstehen. Die Ergebnisse sind in folgender Tabelle aufgelistet:
| Menge | 29 | 187 | 361 |
| Kosten | 926 | 2291 | 4743 |
#1294 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Die Gewinnfunktion eines Produktes lautet $G(x)=-0.43 x^2+29.2x-237$. Die Preisfunktion hat die Gleichung $p(x)=40.9-0.14x$. Bestimme die zugehörige Kostenfunktion.
#1363 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Für einen Artikel wurde folgende Preis-Absatz-Funktion ermittelt:
$$p(x)=-5.4 \cdot 10^{-8}\cdot x^2 - 0.004\cdot x + 18.4$$
Derzeit wird der Artikel um 15 €/Stk verkauft. Um wie viel muss der Preis gesenkt werden, damit 2000 Stück verkauft werden können?
7. Vermischte Aufgaben
#328 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Nachfolgend ist der Graph einer quadratischen Funktion mit der Gleichung $f(x)=ax^2+bx+c$ abgebildet:
Wähle jeweils die zutreffende Eigenschaft aus:
a>0 a=0 a<0
b=0 b≠0
c>0 c=0 c<0
#436 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Wandle die Funktionsgleichung $s(t)=t^2-12t+20$ in die Scheitelpunktform um und gib einen handschriftlichen Lösungsweg an.
#1433 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Ein Stein wird von einer 50 m hohen Brücke fallen gelassen. Seine Höhe über dem Wasser wird durch $h(t)=50-4{,}9t^2$ beschrieben, wobei $t$ in Sekunden und $h(t)$ in Metern gemessen wird.
a) Berechne die mittlere Geschwindigkeit während der ersten und der zweiten Sekunde des Falls in der Einheit km/h.
b) Interpretiere die negativen Vorzeichen der Ergebnisse von Aufgabe a).
c) Berechne, nach welcher Zeit der Stein auf der Wasseroberfläche auftrifft.
d) Zeichne das zugehörige Höhe-Zeit-Diagramm. Berechne dazu die Höhe zu allen ganzen Sekunden und verwende außerdem das Ergebnis aus Frage b).
#1434 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Ein Ball wird aus 1.8 m Höhe senkrecht nach oben geschossen. Nach 2 s erreicht der Ball in 21.5 m Höhe seinen höchsten Punkt.
a) Bestimme die Funktionsgleichung in der Form $h(t)=a\cdot t^2 +b\cdot t +c$, wobei $t$ in Sekunden und $h(t)$ in Metern gemessen wird.
b) Berechne, nach wie vielen Sekunden der Ball am Boden landet.
| Urheberrechtshinweis: Die auf dieser Seite aufgelisteten Aufgaben unterliegen dem Urheberrecht (siehe Impressum). |