Aufgaben zu linearen Gleichungssystemen
Auf dieser Seite befinden sich Aufgaben zu linearen Gleichungssystemen. Jede Aufgabe besitzt eine Nummer, über welche sie durch die Suchfunktion jederzeit wieder aufgerufen werden kann. Dazu muss als Suchbegriff die Aufgabennummer mit einer Raute davor eingegeben werden, also z. B. #123. Die Aufgaben dieser Internetseite werden in jeder Session – also nach jedem Neustart des Webbrowsers oder nach jedem neuen Login – neu generiert. Bei den meisten Aufgaben bedeutet dies, dass sich einzelne Zahlenwerte verändern. Möchte man zu einem späteren Zeitpunkt erneut auf exakt dieselbe Aufgabe zugreifen, so sollte daher ein Screenshot angefertigt werden.
Inhaltsverzeichnis
1. Rechnerische Lösungsverfahren für zwei Variablen
Löse das folgende lineare Gleichungssystem.
[1] $9 x+ 5 y= 10$
[2] $3 x- 8 y= 11$
Löse das folgende lineare Gleichungssystem.
[1] $5 x-20 \cdot (x-10)=5 y$
[2] $(x-10)\cdot (y+ 5)=(x+9)\cdot (y- 5)$
2. Allgemeine Textaufgaben (zwei Variablen)
Das Einkommen von Herrn Gruber und Frau Kern setzt sich aus demselben Grundgehalt und der Abgeltung der geleisteten Überstunden zusammen. Herr Gruber leistet 18 Überstunden und erhielt letztes Monat insgesamt 2888 Euro. Frau Kern leistete 33 Überstunden und erhielt 3402 Euro. Berechne das Grundgehalt sowie die Abgeltung pro Überstunde.
Es fahren 78 Schüler auf Wintersportwoche. Diese verteilen sich auf insgesamt 23 Zimmer, wobei nur Drei- und Vierbettzimmer zur Verfügung stehen. Wie viele Zimmer gibt es von jeder Sorte, wenn alle Zimmer voll belegt sind?
#230 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Zwei Gläser Cola und drei Gläser Eistee kosten 10.60 €. Fünf Gläser Cola und ein Glas Eistee kosten 13.50 €. Bestimme den Preis der beiden Getränke!
Mischt man 2 Liter kaltes Wasser mit 3 Liter heißem Wasser, so erhält man eine Mischung mit einer Temperatur von 45 °C. Durch Mischen von 4 Liter kaltem und einem Liter heißen Wasser erhält man hingegen Wasser mit einer Temperatur von 18 °C. Welche Temperatur hatten das kalte und das heiße Wasser?
Valentin kauft einen Gürtel und ein Paar Schuhe um insgesamt 127 €. Die Schuhe kosten um 100 € mehr als der Gürtel. Wie viel kosten die beiden Produkte jeweils?
#238 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Lies dir das folgende Gespräch zweier Hirten durch und berechne, wie viele Schafe jeder Hirte besitzt!
▪
Hirte A: „Wenn du mir fünf Schafe aus deiner Herde gibst, dann habe ich genauso viele Schafe wie du.“ ▪
Hirte B: „Wenn du mir drei von deinen Schafen gibst, dann habe ich doppelt so viele wie du.“
#270 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
In einem Unternehmen arbeiten dreimal so viele Männer wie Frauen bzw. anders ausgedrückt um 58 Männer mehr als Frauen.
a) Kreuze alle zutreffenden Aussagen an, wenn $x$ die Anzahl der Männer und $y$ die Anzahl der Frauen beschreibt.
$x-y=58$
$y-x=58$
$x=3y$
$y=3x$
b) Berechne, wie viele Männer und wie viele Frauen in diesem Unternehmen arbeiten.
Bei einem Test mit 10 Fragen kann man maximal 44 Punkte erhalten. Der Test besteht aus 3-Punkt-Fragen und aus 5-Punkt-Fragen. Wie viele Fragen gibt es von jeder Sorte?
Eine vierköpfige Familie verbrauchte im März 18 m³ Wasser und zahlte dafür 33.5 €. Im Juli verbrauchte sie 23.3 m³ Wasser und zahlte 43.2 €. Die Monatskosten setzen sich jeweils aus monatlicher Grundgebühr und den Kosten pro Kubikmeter Wasser zusammen. Berechne die Grundgebühr und die Kosten pro Kubikmeter.
Markus und Isabella bekommen das gleiche monatliche Grundeinkommen. Markus leistete 7 Überstunden und bekam insgesamt 2718 €. Isabella leistete 14 Überstunden und bekam insgesamt 3051 €. Wie groß ist das Grundeinkommen der beiden und wie viel bekommen sie pro Überstunde?
#811 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Ein betrügerischer Online-Händler verkauft pro Monat 295 billige Fälschungen eines Notebook-Netzteils als vermeintliche Originalware. Gibt es keine Beschwerden des Käufers (da er es nicht bemerkt oder er sich die damit verbundenen Umstände ersparen möchte), so macht der Händler pro Netzteil einen Gewinn von 7,50 €. Bei einer Beschwerde beträgt der durchschnittliche Verlust hingegen 5,30 €. Nach einem Monat beträgt der Gesamtgewinn 1841,30 €. Wie viele der 295 Käufer beschwerten sich?
3. Geometrische Aufgaben (zwei Variablen)
Ein gleichschenkliges Dreieck hat einen Umfang von 10.2 cm. Die Länge der Basis $c$ entspricht nur einem Drittel der Länge eines Schenkels $a$. Berechne die Länge der Schenkel und der Basis.
#815 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Die Summe der Flächeninhalte zweier Quadrate beträgt 316.9 cm². Die Differenz der Flächeninhalte beträgt 139 cm². Berechne die Seitenlängen der beiden Quadrate.
Eine Seitenlänge eines rechteckigen Grundstücks ist um 5.9 m größer als die andere. Verlängert man beide Seiten um 2.8 m, so wird der Flächeninhalt um 157.3 m² größer. Berechne die ursprünglichen Seitenlängen des Grundstücks!
4. Lösungsfälle (zwei Variablen)
Ergänze die Lücken des folgenden linearen Gleichungssystems so, dass dieses unendlich viele Lösungen besitzt.
[1] $2a+5b=54$
[2] $18a+\,\underline{\,\,\,\,\,\,\,\,\,\,\,}\,\,b=\,\underline{\,\,\,\,\,\,\,\,\,\,\,}$
5. Grafisches Lösungsverfahren (zwei Variablen)
#1240 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Löse das folgende lineare Gleichungssystem grafisch!
[1] $5 x+ 6 y= 1$
[2] $6 x- 5 y= 4$
6. Bewegungsaufgaben (zwei Variablen)
Ein Motorboot fährt bei gleicher Motorleistung flussaufwärts mit einer Geschwindigkeit von 31.4 km/h und flussabwärts mit 44.8 km/h. Wie groß sind die Eigengeschwindigkeit des Bootes und die Fließgeschwindigkeit des Flusses?
Ein Autofahrer und ein Motorradfahrer wohnen 368 km voneinander entfernt und fahren einander entgegen. Wenn beide um 8:00 Uhr wegfahren, treffen sie einander um 10:28 Uhr. Fährt der Motorradfahrer um 8:00 Uhr weg, aber der Autofahrer erst um 9:30 Uhr, so begegnen sie einander um 11:17 Uhr. Berechne die mittleren Geschwindigkeiten beider Fahrzeuge!
7. Lineare Gleichungssysteme mit mehr als zwei Variablen
Löse das folgende lineare Gleichungssystem.
[1] $x+2y+z=20$
[2] $7x+y-z=-12$
[3] $x+4y=26$
#819 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Im Mittelalter war es üblich, Tauschhandel zu betreiben. Nachfolgend sind drei Angebote ersichtlich:
▪
Für zwei Rinder und fünf Schafe erhält man 13 Schweine und 1000 Goldstücke. ▪
Für drei Rinder und drei Schweine erhält man neun Schafe. ▪
Für sechs Schafe, acht Schweine und 600 Goldstücke erhält man fünf Rinder.
a) Erstelle ein lineares Gleichungssystem, welches dazu geeignet ist, zu berechnen, wie viele Goldstücke jedes der drei Tiere wert ist. Gib an, wofür die verwendeten Variablen stehen.
b) Berechne den Wert der drei Tiere:
Bei der sogenannten Dreieck-Stern-Transformation wird eine dreieckförmige Anordnung von Widerständen in eine gleichwertige sternförmige Anordnung umgewandelt.
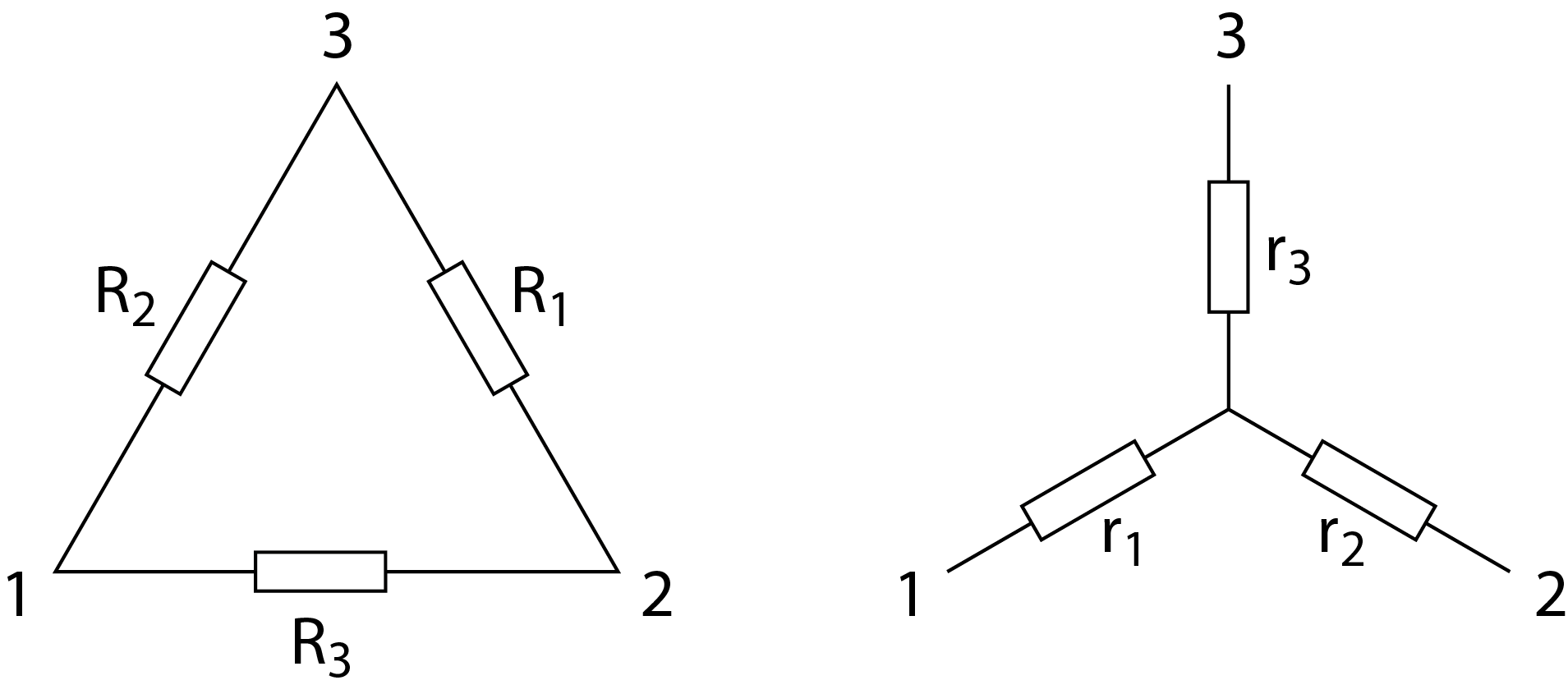
Dafür gelten die folgenden Zusammenhänge:
$$r_1+r_2=\frac{R_3\cdot (R_1+R_2)}{R_1+R_2+R_3}\hspace{1cm}r_2+r_3=\frac{R_1\cdot (R_2+R_3)}{R_1+R_2+R_3}\hspace{1cm}r_1+r_3=\frac{R_2\cdot (R_1+R_3)}{R_1+R_2+R_3}$$
Berechne die Widerstände $r_1,r_2,r_3$ der sternförmigen Schaltung, wenn die Widerstände der Dreiecksschaltung folgende sind: $R_1=23\,\Omega$, $R_2=36\,\Omega$, $R_3=53\,\Omega$.
Gegeben ist die unten abgebildete elektrische Schaltung, wobei $U=29.3\,\mathrm{V}$, $R_1=2.5\,\Omega$, $R_2=3.4\,\Omega$ und $R_3=6.4\,\Omega$ bekannt sind.
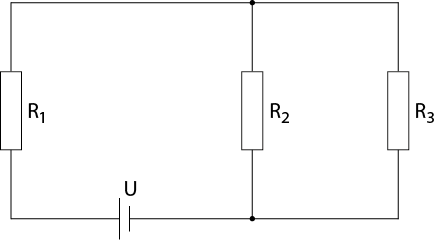
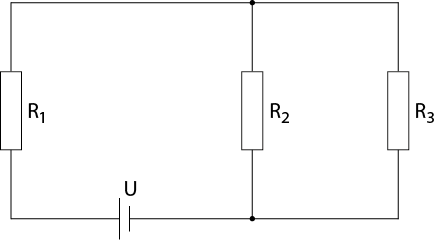
Anhand der Kirchhoffschen Regeln (Knotenregel und Maschenregel) sowie des Ohmschen Gesetzes können folgende Zusammenhänge festgestellt werden:
$$I_1=I_2+I_3\hspace{15mm} I_1R_1+I_3R_3=U \hspace{15mm} I_2R_2=I_3R_3$$
Bereche die Ströme $I_1,I_2$ und $I_3$, welche durch die jeweiligen Widerstände fließen.
#851 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Addiert man je zwei Seitenlängen eines Dreiecks, so erhält man die Ergebnisse 20.7 cm, 13.1 cm und 27.3 cm.
a) Erkläre, wie man den Umfang des Dreiecks berechnen kann, ohne zuvor die einzelnen Seitenlängen zu berechnen.
b) Berechne die Seitenlängen des Dreiecks.
#905 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Addiert man jeweils zwei Winkel eines ebenen Dreiecks, so erhält man 115°, 147° und 98°.
a) Berechne die drei Winkel des Dreiecks.
b) Erkläre, warum diese Aufgabe mehr Information enthält, als man für die Lösung tatsächlich benötigt.
#1147 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Addiert man jeweils zwei Winkel eines ebenen Dreiecks, so erhält man 122° und 145.3°. Berechne die drei Winkel des Dreiecks.
8. Lineare Gleichungssysteme mittels Matrizen lösen
Es ist das folgende Gleichungssystem gegeben:
[1] $5a+6b+5c=2$
[2] $-2a+b=7$
[3] $5a-6b+c=-4$
Verwende die Cramersche Regel, um die Variable $c$ zu bestimmen.
#1276 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Löse das folgende lineare Gleichungssystem mit Hilfe der inversen Matrix.
[1] $5 x+ 8 y= 6$
[2] $2 x- 3 y= -1$
#1277 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Es ist das folgende lineare Gleichungssystem gegeben:
[1] $2x+ 3y= 4$
[2] $6x+ 9y= -11$
a) Berechne die Determinante der zugehörigen Koeffizientenmatrix.
b) Erkläre, wie man anhand dieser Determinante erkennen kann, dass dieses Gleichungssystem keine eindeutige Lösung besitzt.
9. Vermischte Aufgaben
#80 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
In einem Fast-Food-Restaurant wurden folgende Bestellungen aufgegeben:
▪
3 Cheeseburger und 2 Portionen Pommes kosten insgesamt 11,40 €. ▪
2 Cheeseburger und 4 Portionen Pommes kosten insgesamt 16,40 €.
Berechne jeweils den Preis für einen Cheeseburger und für eine Portion Pommes.
#253 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Eine Zirkusvorstellung wird von insgesamt 208 Menschen besucht, wobei der Zirkus durch Ticketverkäufe insgesamt 1931 € verdient. Ein Kinderticket kostet 7 € und für Erwachsene kostet der Eintritt 12 €. Berechne, wie viele Kinder und wie viele Erwachsene in dieser Vorstellung waren.
#1300 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Bei Fußball-Weltmeisterschaften sind in der Gruppenphase jeweils vier Mannschaften pro Gruppe. Es spielt jede Mannschaft einmal gegen jede andere Mannschaft. Dabei erhält man pro Sieg 3 Punkte und pro Unentschieden 1 Punkt. In der nachfolgenden Tabelle ist ersichtlich, welche Mannschaft wie viele Punkte erreichte:
| Team | Punkte | Siege | Unentschieden | Niederlagen |
| A | 7 | |||
| B | 5 | |||
| C | 3 | |||
| D | 1 |
#1454 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Es sollen 1000 Liter einer neuen Fruchtsaftmischung aus Apfelsaft, Kirschsaft und Johannisbeersaft erstellt werden. Dabei sollen Apfelsaft und Kirschsaft zusammen 85 % der Gesamtmenge ausmachen. Der Anteil des Kirschsafts soll doppelt so groß sein, wie jener des Johannisbeersafts. Berechne die erforderliche Menge der drei Sorten.