Aufgaben zu linearen Funktionen
Auf dieser Seite befinden sich Aufgaben zu linearen Funktionen. Jede Aufgabe besitzt eine Nummer, über welche sie durch die Suchfunktion jederzeit wieder aufgerufen werden kann. Dazu muss als Suchbegriff die Aufgabennummer mit einer Raute davor eingegeben werden, also z. B. #123. Die Aufgaben dieser Internetseite werden in jeder Session – also nach jedem Neustart des Webbrowsers oder nach jedem neuen Login – neu generiert. Bei den meisten Aufgaben bedeutet dies, dass sich einzelne Zahlenwerte verändern. Möchte man zu einem späteren Zeitpunkt erneut auf exakt dieselbe Aufgabe zugreifen, so sollte daher ein Screenshot angefertigt werden.
Inhaltsverzeichnis
1. Allgemeine Aufgaben
Bestimme die Parameter $k$ und $d$, sodass der Funktionsgraph der linearen Funktion $f(x)=k\cdot x+d$ durch die vorgegebenen Punkte verläuft.
a) $A(3.2 \mid 4.8)$ und $B(4.5 \mid 2.1)$
b) $S(-1.7 \mid 1.4)$ und $T(5 \mid -3.1)$
Bestimme die Funktionsgleichungen der beiden linearen Funktionen $f$ und $g$, welche folgende Eigenschaften erfüllen.
▪ Der Schnittpunkt der beiden Funktionsgraphen ist der Punkt $(-2.5\mid 2.8)$.
▪ Der Graph von $f$ schneidet die $y$-Achse beim Wert 4.7.
▪ Die Nullstelle von Funktion $g$ ist an der Stelle 4.6.
#1216 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Nachfolgend sind drei Funktionsgraphen von linearen Funktionen abgebildet. Ermittle jeweils die zugehörige Funktionsgleichung.

2. Wachstums- und Abnahmeprozesse
Jemand wartet darauf, dass der Download seines neuen Computerspiels abgeschlossen ist. Vor 50 Minuten fehlten noch 8.3 GB. Aktuell fehlen noch 5.1 GB. Es wird angenommen, dass die Downloadgeschwindigkeit konstant ist, also ein linearer Zusammenhang zwischen fehlender Datenmenge und Zeit besteht.
a) Wie viel wird in 30 Minuten noch fehlen?
b) In wie vielen Minuten wird der Download abgeschlossen sein?
Ein Schwimmbecken wird mit Wasser gefüllt. Um 13:14 Uhr betrug der Wasserstand 53 cm. Um 16:55 Uhr betrug er 1.08 m. Zu welcher Uhrzeit wird die vollständige Füllhöhe von 1.66 m erreicht sein? Gib das Ergebnis im Format HH:MM an.
Die Bevölkerung Brasiliens wächst seit 1950 annähernd linear. Im Jahr 2000 lebten dort ca. 176 Mio. Menschen. Im Jahr 2015 waren es etwa 208 Mio. Menschen. Wie groß wird die Einwohnerzahl im Jahr 2034 sein, wenn man annimmt, dass weiterhin ein lineares Wachstum vorliegt?
Eine aktuell 17.2 cm dicke Schneeschicht schmilzt pro Stunde um 10 mm.
a) Wie dick wird die Schneeschicht nach 5.7 Stunden noch sein?
b) Nach wie vielen Stunden wird der Schnee vollständig geschmolzen sein?
Eine Kerze brennt pro Stunde 2.4 cm nieder. Zu Beginn ist sie 31 cm hoch. Nach welcher Zeit ist die Kerze nur noch 10 cm hoch, wenn man von einem linearen Zusammenhang ausgeht?
Herr Maier hat derzeit 780 Liter Heizöl in seinem Tank und benötigt pro Tag ungefähr 5.8 Liter. Frau Kern hat aktuell 1179 Liter Heizöl in ihrem Tank und benötigt pro Tag ca. 13.1 Liter.
a) In wie vielen Tagen werden beide Personen gleich viel Öl in ihren Tanks haben?
b) Für wie viele Tage reicht Herrn Maiers Vorrat noch?
c) Frau Kern möchte neues Heizöl bestellen, wenn sie nur noch 150 Liter im Tank hat. In wie vielen Tagen wird es soweit sein?
3. Bewegungsaufgaben
Die Donau hat zwischen Linz und Wien eine Länge von 215 km. Ein Schiff startet um 11:40 Uhr in Linz und fährt Richtung Wien mit einer Geschwindigkeit von 17.8 km/h. Zur selben Uhrzeit startet ein anderes Schiff von Wien Richtung Linz mit einer Geschwindigkeit von 11.2 km/h.
a) Erstelle ein Weg-Zeit-Diagramm, welches die Entfernung der beiden Schiffe von Wien veranschaulicht.
b) Zu welcher Uhrzeit fahren die beiden Schiffe aneinander vorbei? Gib das Ergebnis im Format HH:MM an!
c) In welcher Entfernung von Wien findet das Aufeinandertreffen statt?
d) Zu welcher Uhrzeit erreicht das Linzer Schiff Wien? Gib das Ergebnis im Format HH:MM an!
#1028 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Philipp und Clemens fahren mit dem Rad vom selben Ort weg in dieselbe Richtung. Philipp beginnt um 14:10 Uhr mit einer konstanten Geschwindigkeit von 17.6 km/h. Clemens startet um 10 Minuten später und fährt mit 22.4 km/h.
a) Erstelle eine vollständig beschriftete Skizze eines Weg-Zeit-Diagramms, welches beide Aktivitäten veranschaulicht.
b) Zu welcher Uhrzeit (im Format HH:MM) und in welcher Entfernung vom Startpunkt treffen sie sich?
4. Parallele und normale Geraden
Bestimme die Funktionsgleichung $f(x)=k\cdot x+d$ einer linearen Funktion, deren Graph senkrecht auf den Graphen der Funktion $g(x)=-0.8 \cdot x+3.2$ steht und durch den Punkt $P(\,2 \mid 7\,)$ verläuft.
#1346 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Die Gerade $f$ verläuft durch die Punkte $A(-3\mid -2)$ und $B(5\mid 1)$. Die Gerade $g$ ist parallel zu $f$ und verläuft durch den Punkt $C(3 \mid 4)$. Bestimme rechnerisch die Funktionsgleichung von $g$.
5. Stückweise definierte Funktionen
#630 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
In Österreich gibt es seit 2021 bei der Einkommensteuer sieben Tarifzonen, von denen die ersten vier folgendermaßen aussehen:
▪
0 % für jenen Teil bis 11.000 € ▪
20 % für jenen Teil zwischen 11.000 € und 18.000 € ▪
35 % für jenen Teil zwischen 18.000 € und 31.000 € ▪
42 % für jenen Teil zwischen 31.000 € und 60.000 €
a) Erstelle die Funktionsgleichung einer stückweise lineare Funktion, die jedem Bruttojahreseinkommen zwischen 0 und 60.000 € das zugehörige Nettojahreseinkommen zuordnet.
b) Zeichne den Funktionsgraphen dieser Funktion im Intervall $[0, 60\,000]$ entweder auf Papier oder mit einem geeigneten Computerprogramm.
c) Berechne das Nettojahreseinkommen einer Person, die ein Bruttojahreseinkommen von 36000 € hat.
d) Frau Edlinger hatte letztes Jahr ein Nettojahreseinkommen von 30900 €. Wie hoch war ihr Bruttojahreseinkommen?
#638 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Bestimme die Funktionsgleichung des abgebildeten Funktionsgraphen.
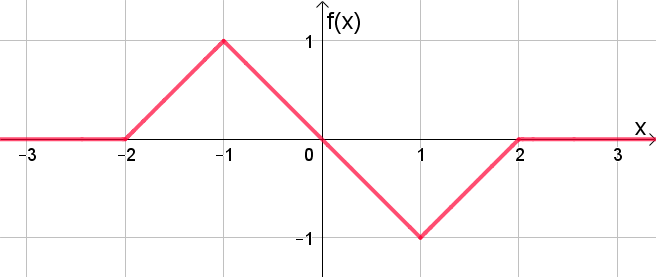
#1148 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Zeichne den Funktionsgraphen der folgenden stückweise definierten Funktion.
$$f(x)=
\begin{cases}
\frac{3}{4}x+4,& \textrm{falls }x\in [-7,-1)\\
2x-4,& \textrm{falls }x\in [-1,3)\\
-\frac{1}{4}x+3,& \textrm{falls }x\in [3,5]\\
\end{cases}
$$
6. Vermischte Aufgaben
Die beiden Tanks A und B sind am Boden durch einen Schlauch verbunden. Zu Beginn ist Tank A vollständig mit Öl gefüllt und Tank B ist leer. Öffnet man das Ventil, so fließt so lange Öl
aus Tank A in Tank B, bis beide Tanks gleich hoch gefüllt sind. Die Füllhöhe der beiden Tanks (in Meter) lässt sich während dieses Vorgangs durch die Funktionen $h_A(t) = 1.78 - 0.1t$ und $h_B(t) = 0.18t$ beschreiben, wobei $t$ die Zeit in Minuten nach dem Öffnen ist.
a) Wie hoch ist der Ölstand zu Beginn in Tank A?
b) Berechne, nach welcher Zeit die Füllhöhe in beiden Tanks ausgeglichen ist.
c) Wie lautet am Ende der Füllstand beider Tanks?
#1201 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Die Einwohnerzahl einer Stadt hat sich folgendermaßen entwickelt:
▪
2006: 32375 Einwohner ▪
2011: 35736 Einwohner ▪
2020: 42471 Einwohner
a) Überprüfe und begründe nachvollziehbar, ob es sich um ein lineares Bevölkerungswachstum handelt.
b) Wie viele Einwohner müssten 2020 in dieser Stadt leben, damit es sich um ein lineares Wachstum handeln würde?
#1210 |
Lösung anzeigen · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Es sind nachfolgend drei Wertepaare vorgegeben:
▪
$x=1.1,\,\,\,y=3$ ▪
$x=4.4,\,\,\,y=5$ ▪
$x=12.5,\,\,\,y=7$
a) Überprüfe nachweislich, ob es sich bei diesen Wertepaaren um einen linearen Zusammenhang handelt. Beschreibe das Ergebnis der Überprüfung durch einen vollständigen Satz.
b) Welchen $y$-Wert müsste der dritte Punkt haben, damit es sich um einen linearen Zusammenhang handeln würde?
Möglichkeiten zur Unterstützung
© 2016 – 2024 MATHE.ZONE