Aufgaben zum Elektromagnetismus
Auf dieser Seite befinden sich Aufgaben zum Elektromagnetismus. Jede Aufgabe besitzt eine Nummer, über welche sie durch die Suchfunktion jederzeit wieder aufgerufen werden kann. Dazu muss als Suchbegriff die Aufgabennummer mit einer Raute davor eingegeben werden, also z. B. #123. Die Aufgaben dieser Internetseite werden in jeder Session – also nach jedem Neustart des Webbrowsers oder nach jedem neuen Login – neu generiert. Bei den meisten Aufgaben bedeutet dies, dass sich einzelne Zahlenwerte verändern. Möchte man zu einem späteren Zeitpunkt erneut auf exakt dieselbe Aufgabe zugreifen, so sollte daher ein Screenshot angefertigt werden.
Inhaltsverzeichnis
Gegeben ist der elektrische Widerstand R = 314 kΩ und die Stromstärke I = 93 µA. Berechne mit dem Ohmschen Gesetz $U = R \cdot I$ die zugehörige elektrische Spannung in der Einheit Volt (V).
#637 |
keine Lösung vorhanden · Einzelansicht · Projektoransicht · Aufgabe neu generieren · Fehler melden
Das in Europa, Australien und großen Teilen Asiens verwendete Stromnetz hat eine Frequenz von 50 Hz und eine Scheitelspannung von 325 V. Der zeitliche Spannungsverlauf kann somit durch die Funktion $U(t)=325\cdot \sin(2\pi t\cdot 50)$ beschrieben werden. Die Effektivspannung $\hat U$ ist jene Gleichspannung, die am selben Widerstand pro Periode die gleiche elektrische Energie liefert, wie die betrachtete Wechselspannung. Diese Energie ist proportional zur elektrischen Leistung und somit wiederum proportional zu $U^2$. Berechne die Effektivspannung der gegebenen Wechselspannung.
Bei der sogenannten Dreieck-Stern-Transformation wird eine dreieckförmige Anordnung von Widerständen in eine gleichwertige sternförmige Anordnung umgewandelt.
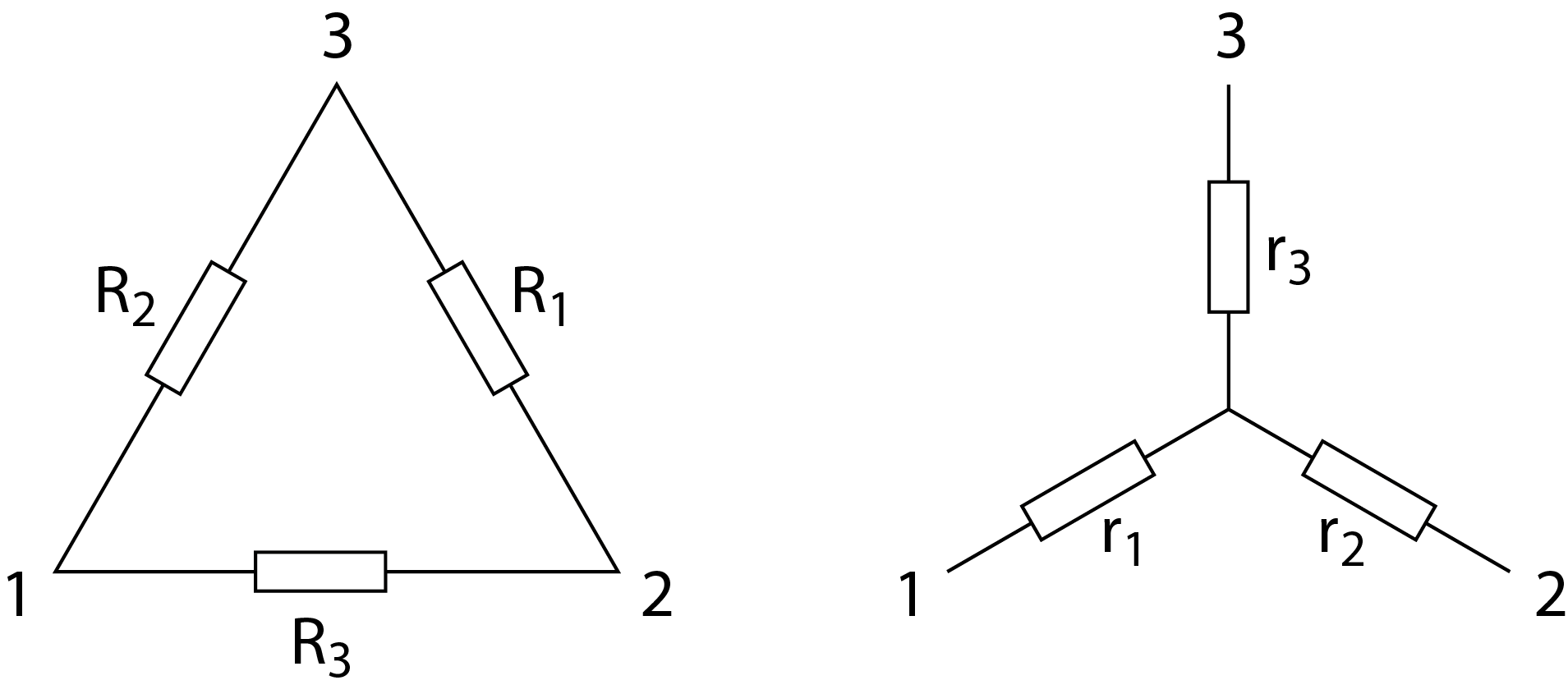

Dafür gelten die folgenden Zusammenhänge:
$$r_1+r_2=\frac{R_3\cdot (R_1+R_2)}{R_1+R_2+R_3}\hspace{1cm}r_2+r_3=\frac{R_1\cdot (R_2+R_3)}{R_1+R_2+R_3}\hspace{1cm}r_1+r_3=\frac{R_2\cdot (R_1+R_3)}{R_1+R_2+R_3}$$
Berechne die Widerstände $r_1,r_2,r_3$ der sternförmigen Schaltung, wenn die Widerstände der Dreiecksschaltung folgende sind: $R_1=22\,\Omega$, $R_2=36\,\Omega$, $R_3=59\,\Omega$.
Gegeben ist die unten abgebildete elektrische Schaltung, wobei $U=30.4\,\mathrm{V}$, $R_1=2.3\,\Omega$, $R_2=3.4\,\Omega$ und $R_3=7\,\Omega$ bekannt sind.
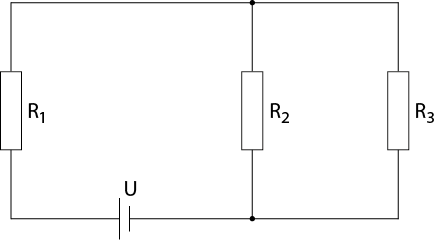
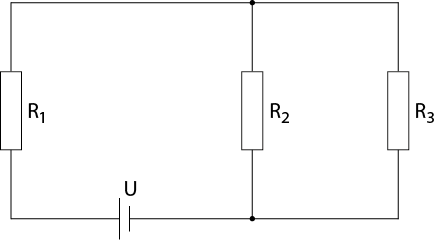
Anhand der Kirchhoffschen Regeln (Knotenregel und Maschenregel) sowie des Ohmschen Gesetzes können folgende Zusammenhänge festgestellt werden:
$$I_1=I_2+I_3\hspace{15mm} I_1R_1+I_3R_3=U \hspace{15mm} I_2R_2=I_3R_3$$
Bereche die Ströme $I_1,I_2$ und $I_3$, welche durch die jeweiligen Widerstände fließen.
Der Ladevorgang eines Handyakkus kann durch eine beschränkte Wachstumsfunktion beschrieben werden. Für ein bestimmtes Handy wurde die Funktion $f(t)=100\cdot \left(1-e^{-0.026t}\right)$ ermittelt, wobei $t$ die Zeit in Minuten angibt und $f(t)$ den zugehörigen Ladestand in Prozent. Zum Zeitpunkt $t=0$ ist der Akku komplett leer.
a) Welchen Ladestand zeigt das Handy nach 21 Minuten Ladezeit?
b) Nach welcher Zeit ist der Akku halb aufgeladen?
c) Wie lange dauert es, bis das Handy einen Ladestand von 100 % anzeigt? Theoretisch wird dieser Wert nie erreicht, jedoch wird ab 99,5 % auf 100 % aufgerundet. Gib das Ergebnis in Stunden an.
d) Das Handy zeigt bereits einen Ladestand von 38 % an. Wie lange dauert es noch, um 70 % zu erreichen?
Möglichkeiten zur Unterstützung
© 2016 – 2024 MATHE.ZONE